Question
(a) Complete the table of values for \(y = x^2 – 3x – 1\).
| x | -2 | -1 | 0 | 1 | 2 | 3 | 4 | 5 |
| y | 9 | -1 |
(b) On the grid, draw the graph of \(y = x^2 – 3x – 1\) for \(-2 \leq x \leq 5\).
(c) Write down the co-ordinates of the lowest point of the graph.
(d) (i) On the grid, draw the line of symmetry of the graph.
(ii) Write down the equation of the line of symmetry of the graph.
Answer/Explanation
Ans:
(a) (9), 3, (–1), –3, –3, –1, 3, 9
(b) completely correct curve
(c) (1.5, k) where –3.5 ⩽ k < –3
(d) (i) ruled line x =1.5 drawn
(ii) x =1.5 oe
Question
(a) Complete the table of values for \(y=\frac{8}{x}\).
(b) On the grid, draw the graph of \(y = \frac{8}{x}\) for \(-8 \leq x \leq -1\) and \(1 \leq x \leq 8\).
(c) The graph of \(y = \frac{8}{x}\) has two lines of symmetry
Write down the equation of each of these lines.
……………………. and ……………………..
(d) Mark a point, P , on the graph of \(y = \frac{8}{x}\) where the x and y co-ordinate are equal.
Answer/Explanation
Answer:
(a) -2, -4, 8, 4
(b) completely correct curve
(c) y = x, y = -x oe
(d) point at (2.8, 2.8) or (-2.8, -2.8)
Question
(a)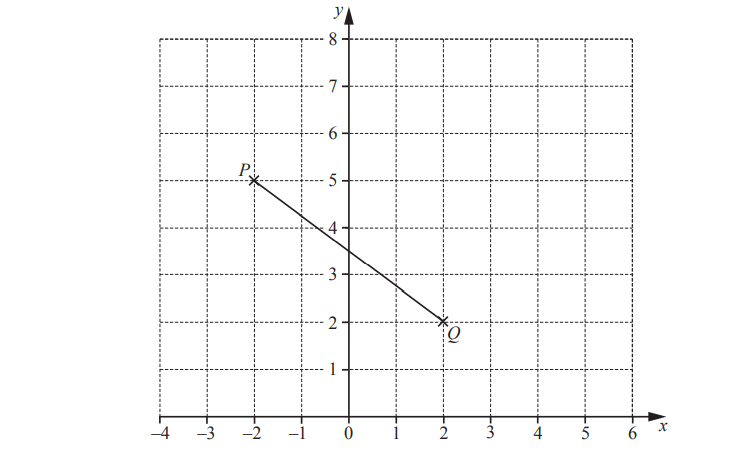
(i) Write down the co-ordinates of point P.
(………………… , …………………)
(ii) Write down the column vector \(\vec{PQ}.\)
(iii)\(\vec{QR}=\begin{pmatrix}3\\ 2\end{pmatrix}\)
On the grid, plot point R
(iv) PQRS is a parallelogram.
On the grid, complete the parallelogram PQRS.
Write down the co-ordinates of point S.
(………………… , …………………)
(b)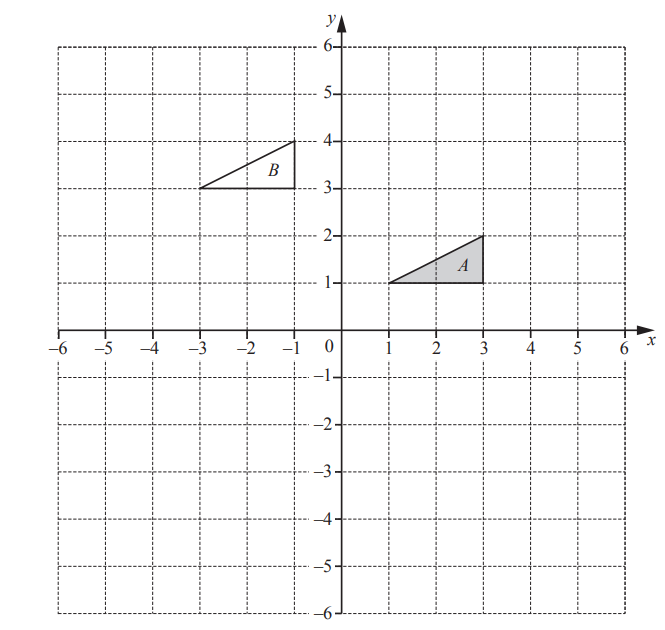
(i) Describe fully the single transformation that maps triangle A onto triangle B.
……………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………..
(ii) On the grid, draw the image of triangle A after a reflection in the line y =-1.
(iii) On the grid, draw the image of triangle A after a rotation through 180° about (0, 0).
Answer/Explanation
(a)(i) (–2, 5)
(ii)\(\begin{pmatrix}4\\ -3\end{pmatrix}\)
(iii) (5, 4) plotted
(iv) Parallelogram PQRS correctly drawn
(1, 7)
(b)(i) Translation
\(\begin{pmatrix}-4\\ 2\end{pmatrix}\)
(ii) Correct reflection
vertices (3, –3), (1, –3), (3, –4)
(iii) Correct rotation
vertices (–3, –1), (–1, –1), (–3, –2)
