Question
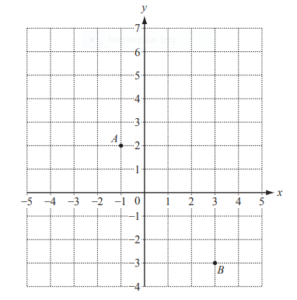
(a) Write down the co-ordinates of point A.
(b) Write \(\overrightarrow{AB}\) as a column vector.
(c) \(\overrightarrow{AC}=\binom{2}{3}\)
Write down the co-ordinates of C.
Answer/Explanation
(a) (–1, 2)
(b)\(\binom{4}{-5}\)
(c) (1, 5)
Question
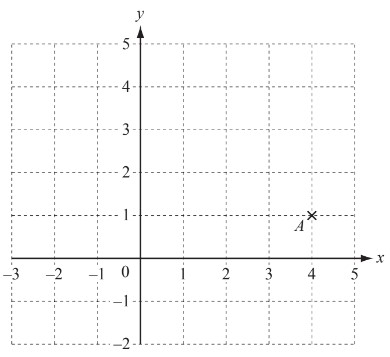
(a) Write down the co-ordinates of point A.
(b) On the grid, plot the point (–1, 3).
Answer/Explanation
Ans:
(a) (4, 1)
(b) Point plotted at (–1, 3)
Question
(a) Write down the co-ordinates of the point where the line y = 3x + 5 crosses the y-axis.
Answer/Explanation
Ans: ( 0 , 5 )
(b) Write down the equation of a line that is parallel to the line y = 3x + 5.
Answer/Explanation
Ans: y = 3x + k
Question
(a)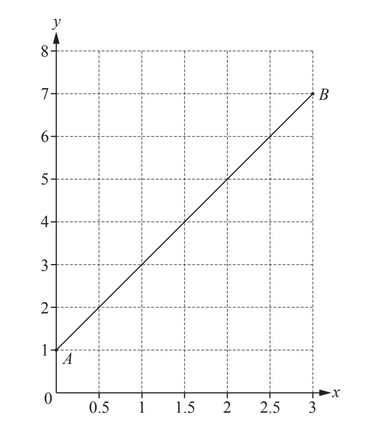
The line AB is drawn on the grid.
(i) Write down the co-ordinates of A.
(ii) Work out the gradient of the line AB.
(iii) Write down the equation of the line AB in the form y = mx + c.
y = ……………….
(b) Write down the equation of a straight line that is parallel to y = 5x – 3.
Answer/Explanation
Ans:
(a) (i) 0, 1
(ii) 2
(iii) [y =] 2x + 1 final answer
(b) y = 5x + c oe final answer
Question
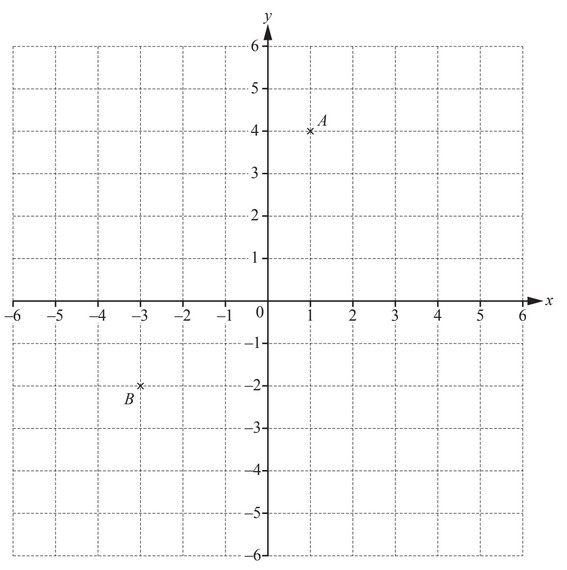
(a) Write down the co-ordinates of point A.
(…………………….. , ……………………..)
(b) Plot the point (5, –2).
Label this point C.
(c) Write down the mathematical name of triangle ABC.
(d) Write \(\overrightarrow{AB}\) as a column vector
\(\overrightarrow{AB}\)= ( )
(e) \(\overrightarrow{BD} = \begin{pmatrix}
-2\\ 5
\end{pmatrix}\)
Write down the co-ordinates of point D.
Answer/Explanation
Ans:
(a) (1, 4)
(b) Point plotted at (5, -2)
(c) Isosceles
(d) \(\begin{pmatrix}
-4\\-6
\end{pmatrix}\)
(e) (-5, 3)
