Question
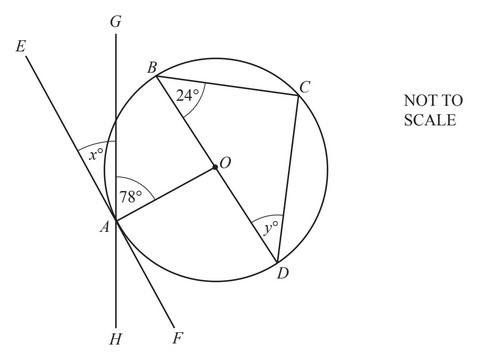
A, B, C and D are points on the circumference of a circle, centre O.
EF is a tangent to the circle at A.
GH is a straight line through the point A.
Angle CBD = 24° and angle OAG = 78°.
(a) (i) Write down the mathematical names of lines BC and OA.
(ii) Find the value of x, giving a reason for your answer.
(iii) Find the value of y, giving a reason for your answer.
(b) The diagram shows a regular polygon, centre O.
(i) Write down the name of this polygon.
(ii) Find the value of w.
Show all your working.
(c) The exterior angle of another regular polygon is 24°.
Calculate the number of sides this polygon has.
Answer/Explanation
Answer:
(a) (i) Chord
Radius
(ii) 12
Tangent [meets] radius [at] 90 [°]
(iii) 66
Angles [in] triangle 180 or
Angle [in a] semi–circle [= 90]
(b) (i) Octagon
(ii) \(360 \div [=45]\)
(180 – their 45) ÷ 2
67.5
(c) 15
Question
(a) A cuboid measures 6cm by 3cm by 2cm.
(i) On this 1 \(cm^2\) grid, complete the net of the cuboid.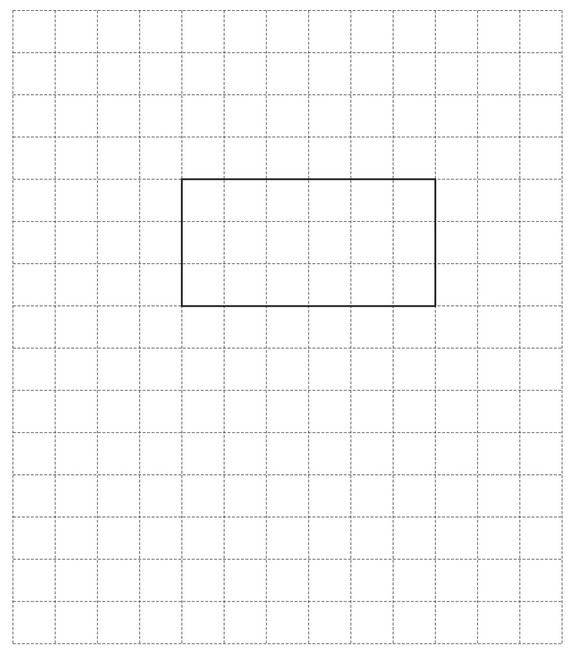
(ii) Calculate the volume of the cuboid.
……………………………. \(cm^3\)
(b) 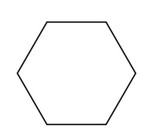
Write down the mathematical name of this shape.
(c) 
Mark an obtuse angle on this trapezium.
(d) A regular polygon has an exterior angle of 22.5°.
Work out how many sides this polygon has.
(e) 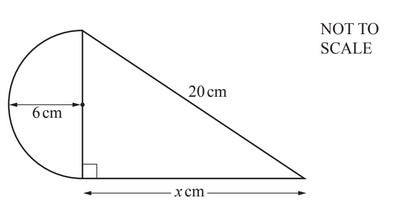
The diagram shows a shape made from a semi-circle, radius 6cm, and a right-angled triangle.
(i) Show that x = 16.
(ii) Calculate the area of the shape.
…………………………… \(cm^2\)
Answer/Explanation
Answer:
(a) (i) Correct net
(ii) 36
(b) Hexagon
(c) Obtuse angel indicated
(d) 16
(e) (i) \(\sqrt{20^2 – 12^2}\)
(ii) 153 or 152.5 to 152.6
Question
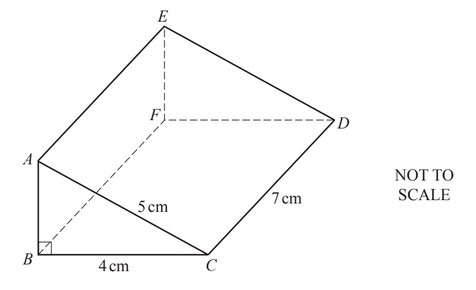
The diagram shows a solid in the shape of a triangular prism.
AC = 5cm, BC = 4cm and CD = 7cm.
Angle ABC = 90°.
(a) What does the word prism tell you about the solid in the diagram?
(b) Show that AB = 3cm.
(c) Calculate the volume of the prism.
Give the units of your answer.
(d) On the 1 \(cm^2\) grid, complete the net of the prism.
Two faces have been drawn for you.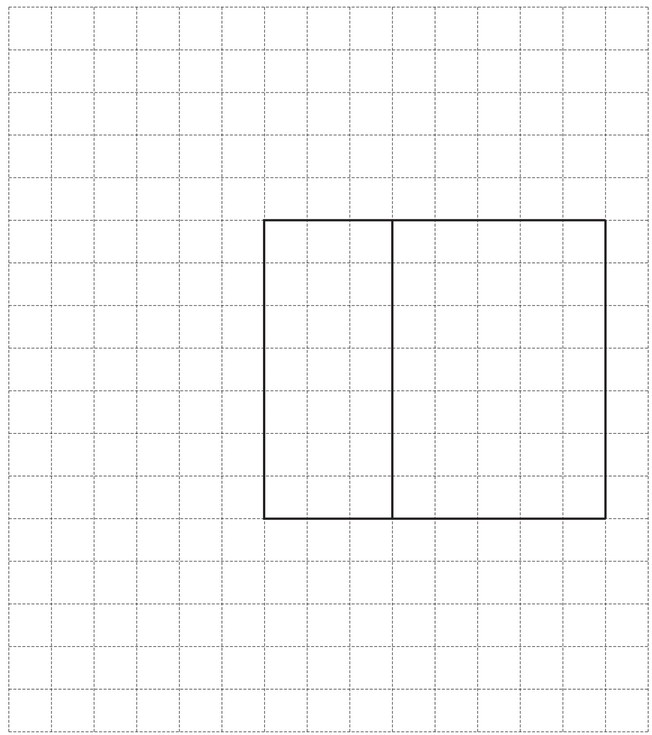
(e) Calculate the surface area of the prism.
………………….. \(cm^2\)
Answer/Explanation
Ans:
(a) constant cross-sectional area oe
(b) \([AB^2]+4^2=5^2\)
\([AB]=\sqrt{5^2-4^2} = \sqrt{9}\)
(c) 42
\(cm^3\)
(d) correct net drawn
(e) 96
