Question
(a)
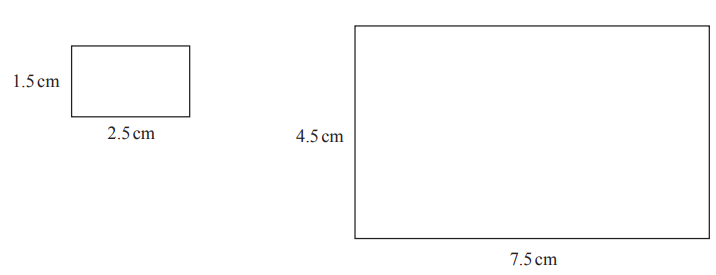
(i) Explain why these rectangles are mathematically similar.
……………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………
(ii) How many times bigger is the area of the large rectangle than the area of the small rectangle?
………….
(b)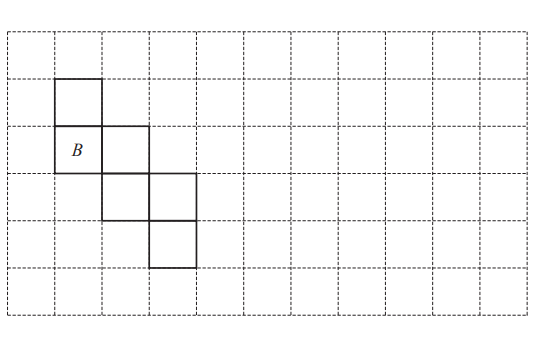
The diagram shows a net of a cube.
(i) The square labelled B is the base.
Write the letter T in the square that is the top of the cube.
(ii) On the grid, draw a different net of this cube.
(c) The diagram shows a cuboid.
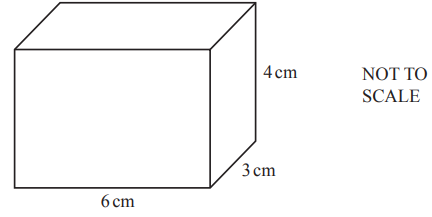
(i) Work out the surface area of this cuboid.
………………………………….. \(cm^{2}\)
(ii) Work out the volume of this cuboid.
………………………………….. \(cm^{3}\)
(iii) Write down the dimensions of a different cuboid that has the same volume as this cuboid.
………………… cm by ………………… cm by ………………… cm
Answer/Explanation
(a)(i)One rectangle is an enlargement of the other.
(ii)9
(b)(i)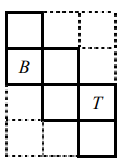 
in correct square
(ii)A different correct net drawn
(c)(i)108
(ii)72
(iii)3 positive numbers (other than 3,4,6) with product 72
Question
(a)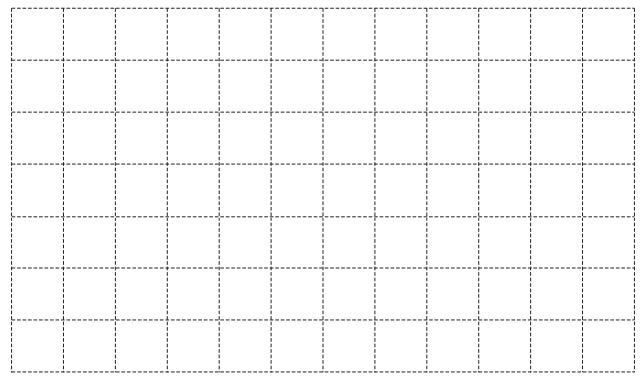
On the \(1cm^{2}\)
grid, draw one rectangle that has
• a perimeter of 22cm
and
• an area of \(24cm^{2}\)
(b)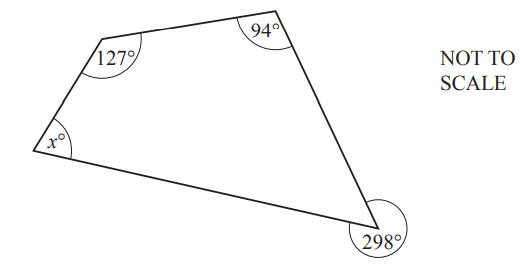
Work out the value of x.
Write down the two geometrical properties needed to find x
1 ………………………………………………………………………………………………………………………………..
2 ………………………………………………………………………………………………………………………………..
x = …………………………………………
(c)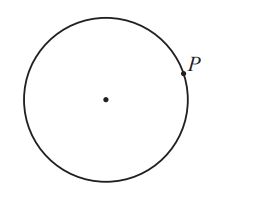
Draw a tangent to the circle at point P.
(d) The exterior angle of a regular polygon is 24°.
Work out the number of sides of this polygon.
………………………………………….
(e)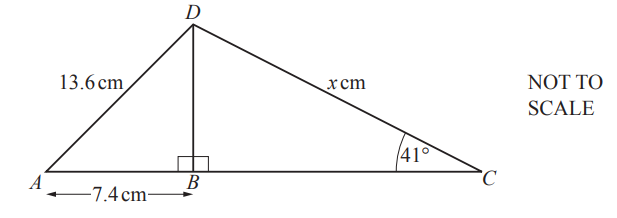
Calculate the value of x.
x = …………………………………………
Answer/Explanation
(a) 8 cm by 3 cm rectangle drawn
(b) 77 with two correct properties
(c) Ruled tangent drawn
(d) 15
(e) 17.4 or 17.39…
Question
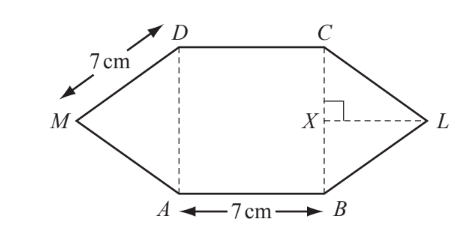
In the diagram, ABCD is a square of side 7 cm. BLC and DMA are equilateral triangles.
(a) Find the perimeter of the shape ABLCDM.
(b) (i) Write down the size of angle CBL.
(ii) Calculate the length of LX.
(c) (i) Calculate the area of triangle BLC.
(ii) Calculate the area of the shape ABLCDM.
▶️Answer/Explanation
(a) 42
(b) (i) $60^{\circ}$
(ii) $6.06(217 \ldots)$
(c) (i) 21.2 to $21.4 \mathrm{ft}$
(ii) 91.4 to $91.7 \mathrm{ft}$