Question
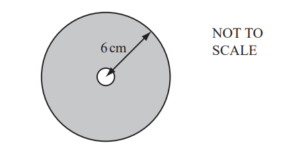
The diagram shows a circular disc with radius 6 cm.
In the centre of the disc there is a circular hole with radius 0.5 cm.
Calculate the area of the shaded section.
Answer/Explanation
Ans: 112 or 112.3 to 112.33
Question
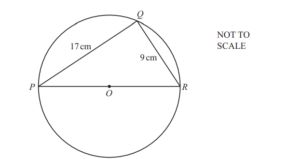
The diagram shows a circle, centre O.
P, Q and R are points on the circumference.
PQ = 17 cm and QR = 9cm.
(a) Explain why angle PQR is 90°.
Answer/Explanation
Ans: Angle [in a] semi-circle
(b) Calculate the length PR.
Answer/Explanation
Ans: 19.2 or 19.23 to 19.24
Question
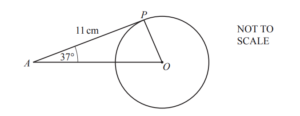
In the diagram, AP is a tangent to the circle at P.
O is the centre of the circle, angle PAO = 37° and AP = 11cm.
(a) Write down the size of angle OPA.
Answer/Explanation
Ans: 90
(b) Work out the radius of the circle.
Answer/Explanation
Ans: 8.29 or 8.289 to 8.29
Question
The diagram shows a circle, centre O.
A, B and C are points on the circumference.
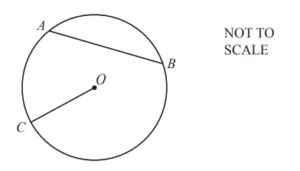
Write down the mathematical name of the straight line
(a) OC,
Answer/Explanation
Ans: radius
(b) AB.
Answer/Explanation
Ans: chord
