Question
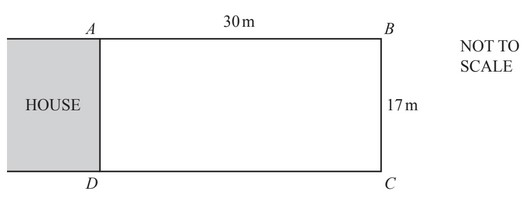
The rectangle ABCD shows Mr Liu’s garden.
(a) Mr Liu puts a fence around three sides of his garden, AB, BC and CD.
The fence costs $3.28 per metre.
Calculate the cost of the fence.
(b) (i) Calculate the area of Mr Liu’s garden.
(ii) Mr Liu uses an area of 408\(m^2\) in his garden for a lawn, flowers and vegetables.
He divides this area into three parts, in the ratio
lawn:fl owers:vegetables = 5:3:4.
Calculate the area used for each part.
(c) Mr Liu walks in a straight line across his garden from A to C.
Calculate the distance Mr Liu walks.
(ii) The pond is fi lled with water to a depth of 2 metres.
Calculate the volume of water in the pond.
Answer/Explanation
Answer:
(a) 252.56
(b) (i) 510
(ii) 170
102
136
(c) 34.5
(d) (i) 63.6 or 63.61 – 63.63
(ii) 127 or 127.2…
Question
(a) Calculate the area of a circle of radius 6cm.
(b) 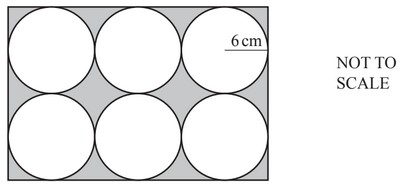
Each circle in this rectangle has a radius of 6cm.
The circles fit exactly in the rectangle.
Calculate the shaded area.
Answer/Explanation
Answer:
(a) 113 or 113.09 to 113.112
(b) 185 or 186 or 185.76
or 185.328 to 185.42
Question
(a) 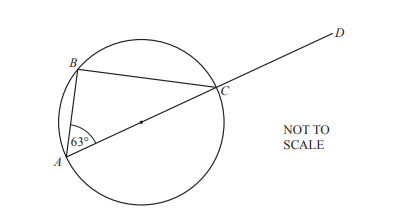
A, B and C lie on a circle with diameter AC.
AC is extended to D and angle BAC = 63°.
Work out angle BCD.
Give reasons to explain your answer.
Answer/Explanation
Ans: 153
two correct geometrical reasons.
(b) 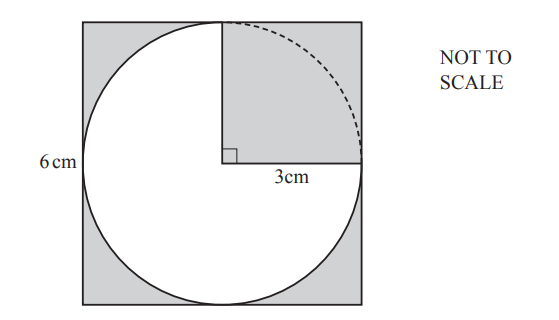
The diagram shows a circle with radius 3cm inside a square of side 6cm.
Calculate the shaded area.
Answer/Explanation
Ans: 14.8
or 14.79 to 14.80
(c) 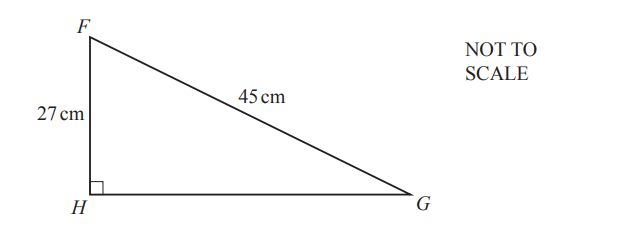
FGH is a right-angled triangle.
Calculate
(i) GH,
Answer/Explanation
Ans: 36 cm
(ii) the perimeter of the triangle,
Answer/Explanation
Ans: 108 cm
(iii) the area of the triangle.
Answer/Explanation
Ans: 486 cm2
Question
(a) The grid shows part of the net of a cuboid.
Complete the net.
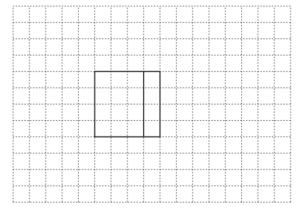
Answer/Explanation
Ans: correct net drawn
(b) The volume of another cuboid is 60cm3.
Each side is a whole number of centimetres long.
Write down a possible set of dimensions for the cuboid.
Answer/Explanation
Ans:
60,1,1 or 30,2,1 or 20,3,1 or
15,4,1 or 15,2,2 or 12,5,1 or
10,6,1 or 10,3,2 or 6,5,2 or
5,4,3
(c) Each side of a cube has length 2cm.
Work out the total surface area of the cube.
Give the units of your answer.
Answer/Explanation
Ans: 24 cm2
(d) Change 9cm2 into mm2.
Answer/Explanation
Ans: 900 mm2
(e) The diagram shows a triangle.
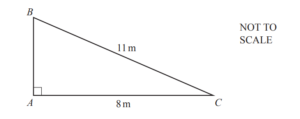
(i) Calculate the length AB.
Answer/Explanation
Ans: 7.55 or 7.549….. m
(ii) Use trigonometry to calculate angle ACB.
Answer/Explanation
Ans: 43.3 or 43.34
(f)
The diameter of the large circle is 13cm.
The radius of the small circle is 2cm.
Calculate the shaded area.
Answer/Explanation
Ans: 120 or 120.16 to 120.2 cm2
Question
(a) (i) Complete the table of values for y = x2+ x – 4.
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -2 | -4 | -2 | 8 |
Answer/Explanation
Ans:
| x | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| y | 8 | 2 | -2 | -4 | -4 | -2 | 2 | 8 |
(ii) On the grid, draw the graph of y = x2+ x – 4 for -4 ≤ x ≤ 3.
Answer/Explanation
Ans: Correctly plotted points and smooth correct curve

(b) (i) Write down the co-ordinates of the lowest point of the graph.
Answer/Explanation
Ans: (–0.5, k) where –4.5 ≤ k < –4
(ii) Write down the equation of the line of symmetry of the graph.
Answer/Explanation
Ans: x = –0.5
(c) Use your graph to solve the equation x2+ x – 4 = –3.
Answer/Explanation
Ans: –1.8 ≤ x ≤ –1.4, 0.4 ≤ x ≤ 0.8
(d)
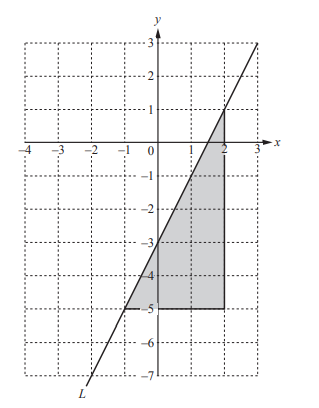
(i) In the diagram, a line L has been drawn on a 1 cm2 grid.
Write down the equation of the line L.
Give your answer in the form y = mx + c.
Answer/Explanation
Ans: 2x – 3
(ii) Find the area of the shaded triangle.
Answer/Explanation
Ans: 9
Question
(a) The table shows the temperature at noon each day for one week in a city.
| Monday | Tuesday | Wednesday | Thursday | Friday | Saturday | Sunday |
| 5°C | 2 °C | −3°C | −1°C | 0 °C | 1°C | −2 °C |
(i) Which day had the lowest noon temperature?
(ii) Find the difference between the noon temperatures on Tuesday and Wednesday.
……………………………………….°C
(iii) Write these seven temperatures in order, starting with the lowest.
(iv) On Sunday the noon temperature was −2°C.
The next day the noon temperature fell by 4°C.
Find the noon temperature on the next day.
(b) The number of houses in the city is 1935 364.
Write this number correct to the nearest million.
(c) The height, h metres, of a tower in the city is 120m, correct to the nearest 10m.
Complete this statement about the value of h.
……………….. G h < ………………..
(d) The diagram shows the cross section of a circular tunnel in the city.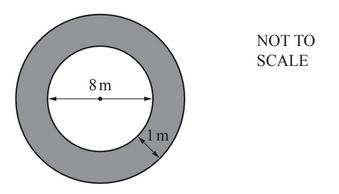
Calculate the shaded area.
Answer/Explanation
Answer:
(a) (i) Wednesday
(ii) 5
(iii) -3 -2 -1 0 1 2 5
(iv) -6
(b) 2 million or 2 000000
(c) 115 125
(d) 28.3 or 28.27 to 28.28
Question
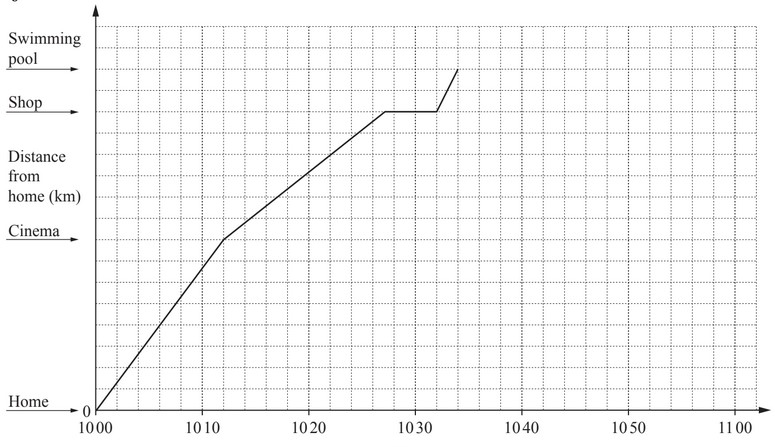
Abjit cycles from his home to the swimming pool.
The travel graph for his journey is drawn on the grid.
On his journey he passes the cinema and the shop.
(a) Write down where Abjit stops on his journey to the swimming pool.
(b) Abjit is cycling fastest between the shop and the swimming pool.
Explain how you know this from looking at the graph.
(c) Abjit cycles at 20km/h from his home to the cinema.
This part of the journey takes 12 minutes.
(i) Show that the distance from Abjit’s home to the cinema is 4km.
(ii) Complete the scale on the vertical axis of the grid by showing at least two other values.
(d) Calculate the speed, in km/h, that Abjit cycles from the cinema to the shop.
………………………………….. km/h
(e) When Abjit arrives at the swimming pool it is closed.
Without stopping at the swimming pool he cycles home at a constant speed.
It takes him 24 minutes to cycle home.
Complete the travel graph for his journey home.
(f) Calculate the average speed, in km/h, for the whole journey.
………………………………….. km/h
(g) Abjit’s bicycle wheel has a radius of 29cm.
(i) Calculate the circumference of the wheel.
Give your answer correct to 1 decimal place.
…………………………………….. cm
(ii) Calculate the number of complete turns the wheel makes when travelling 500m.
Answer/Explanation
Ans:
(a) shop
(b) [graph] steepest oe
(c) (i) \(0.2 \times 20\) or \(12 \times \frac{1}{3}\) oe
(ii) distance axis numbered correctly
with at least 2 more numbers
(d) 12
(e) ruled line from (1034, 8) to
(1058, 0)
(f) 16.6 or 16.55…
(g) (i) 182.2
(ii) 274
Question
(a) A cylinder has a radius of 6cm and a height of 17 cm.
Show that the volume of this cylinder is 1923cm3, correct to 4 significant figures. [2]
(b)
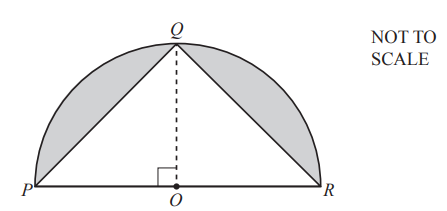
Points P, Q and R are on the circumference of a semicircle, center O and radius 8 cm. Angle POQ = 90°.
Calculate the shaded area.
cm2 [5]
Answer/Explanation
Ans:
8(a) π × 62 × 17
1922.6 to 1922.91
8(b) 36.5 or 36.53 to 36.54…
Question
(a) Using a straight edge and compasses only, construct the equilateral triangle ABC. The base AB has been drawn for you.[2]
![]()
(b)
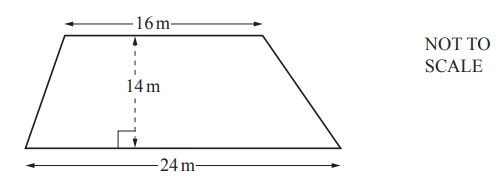
Calculate the area of this trapezium.
m2 [2]
(c) Each interior angle of a regular polygon is 162°.
Calculate the number of sides of the polygon. [3]
(d)
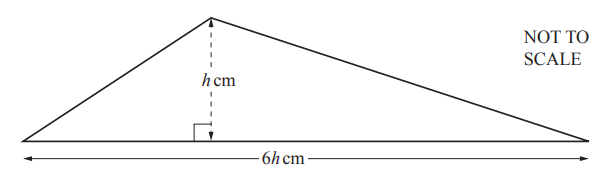
The area of this triangle is 363cm2.
Calculate the value of h.
h = [3]
(e)
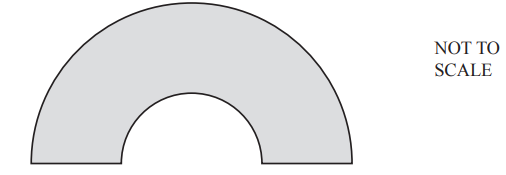
This shape is drawn using two semicircles that have the same center.
The large semicircle has radius 7cm.
The small semicircle has radius 3cm.
Calculate the area of the shape.
cm2 [3]
Answer/Explanation
Ans:
10(a) correct triangle drawn with arcs
10(b) 280
10(c) 20
10(d) 11
10(e) 62.8 or 62.83 to 62.84
Question
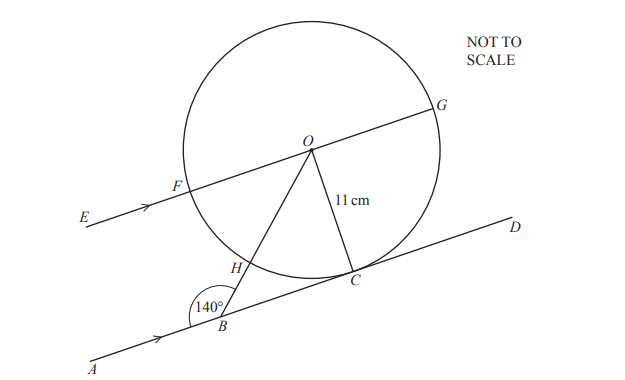
The diagram shows a circle, centre O, radius 11 cm.
C, F, G and H are points on the circumference of the circle.
The line AD touches the circle at C and is parallel to the line EG.
B is a point on AD and angle ABO = 140°.
(a) Write down the mathematical name of the straight line AD.
…………………………………………. [1]
(b) (i) Find, in terms of r, the circumference of the circle.
…………………………………….. cm [2]
(ii) Work out angle FOH.
Angle FOH = ………………………………………….
(iii) Calculate the length of the minor arc FH.
…………………………………….. cm
(c) (i) Give a reason why angle BCO is 90°.
…………………………………………………………………………………………………………………………… [1]
(ii) Show that BC = 13.11 cm, correct to 2 decimal places.
(iii) Calculate BH.
BH =………………………………………………….. cm
Answer/Explanation
(a) Tangent
(b)(i) 22π final answer
(ii) 40
(iii) 7.68 or 7.679 to 7.680….
c)(i) Angle [between] tangent [and] radius
(ii) 180 – 140 or 90
an (180 – 140) = \frac{11}{BC}
BC =] 13.109[…]
(iii) 6.11 or 6.112 to 6.114
Question
(a)
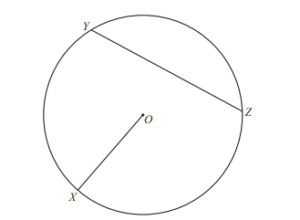
X, Y and Z lie on a circle, centre O.
(i) Write down the mathematical name of the line
(a) OX,
Answer/Explanation
Ans: Radius
(b) YZ
Answer/Explanation
Ans: Chord
(ii) Measure the length of OX.
Answer/Explanation
Ans: 3.5
(b) Another circle has a radius of 18cm.
Calculate the circumference of this circle.
Answer/Explanation
Ans: 113 or 113.09… to 113.112
(c) In this part, all angles are in degrees.
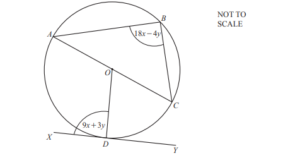
A, B, C and D lie on a circle, centre O, diameter AC.
XY is a tangent to the circle at D.
(i) Use the information in the diagram to complete these two simultaneous equations.
9x + 3y = …………………..
18x – 4y = …………………..
Answer/Explanation
Ans: 90
90
(ii) Solve your simultaneous equations.
You must show all your working.
Answer/Explanation
Ans: For correctly eliminating one variable
[x = ] 7
[y =] 9
Question
The diagram represents a fairground wheel with centre O, and diameter 30 metres. Point D is vertically below point A, and the line EDB is horizontal. ED = 20 metres.
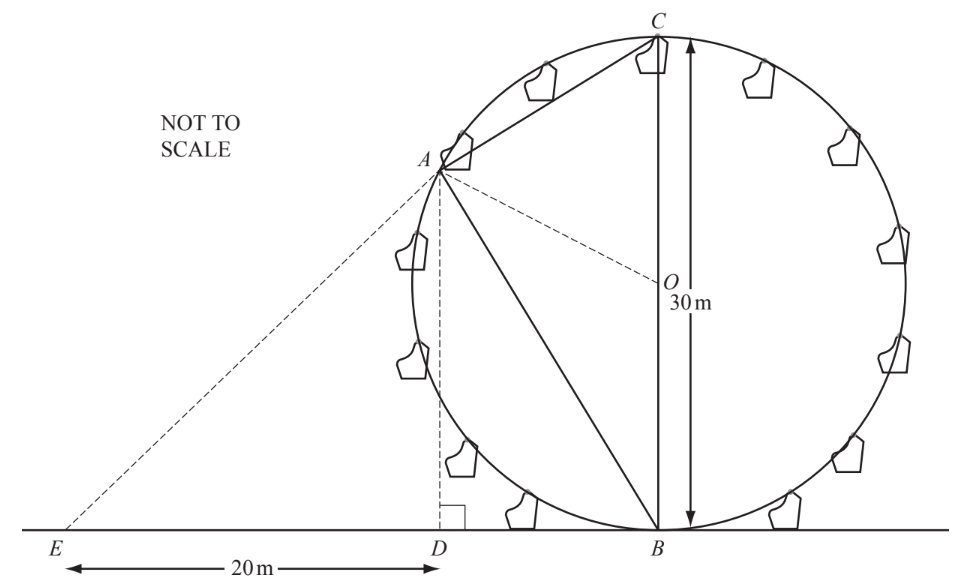
(a) A seat starts at $B$ and travels one-third of the circumference to $A$.
Explain why angle $A O B$ equals $120^{\circ}$.
(b) Find the value, in degrees, of
(i) angle $A B O$,
(ii) angle $B A C$,
(iii) angle $A B D$.
(c) (i) Use trigonometry in triangle ABC to calculate the distance AB.
(ii) Show that $A D=22.5$ metres.
$\operatorname{Answer(c)(ii)~}$
(d) Eshe holds her camera at $E$ and takes a photograph of her friend in the seat at $A$.
Calculate angle $A E D$.
▶️Answer/Explanation
(a) One-third of 360 oe
(b) (i) 30
(ii) 90
(iii) 60
(c) (i) $26(.0)$ or $25.98(\ldots \ldots)$
(ii) (c) (i) $\sin$ (b) (iii) oe 22.5
(d) 48.36 to 48.4