Question
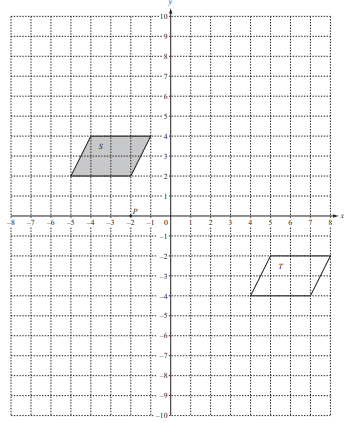
The diagram shows two shapes, S and T, on a 1cm2 grid.
P is the point (–2, 0).
(a) (i) Write down the mathematical name of shape S.
Answer/Explanation
Ans: Parallelogram
(ii) How many lines of symmetry does shape S have?
Answer/Explanation
Ans: 0
(b) Describe the single transformation that maps shape S onto shape T.
Answer/Explanation
Ans: Translation
\(\binom{9}{-6}\)
(c) On the grid,
(i) draw the refl ection of shape S in the y-axis,
Answer/Explanation
Ans: (1, 4), (4, 4), (5, 2), (2, 2).
(ii) draw the rotation of shape S about (0, 0) through 90° anti-clockwise.
Answer/Explanation
Ans: (−4, −1), (−4, −4), (−2, −5), (−2, −2)
(d) On the grid, draw the enlargement of shape S with scale factor 2 and centre P (–2, 0).
Label the image E.
Answer/Explanation
Ans: (–6,8), (0,8), (–8,4), (–2,4)
(e) (i) Work out the area of shape S.
Answer/Explanation
Ans: 6
(ii) How many shapes, identical to shape S, will fi ll shape E completely?
Answer/Explanation
Ans: 4
(iii) Work out the area of shape E.
Answer/Explanation
Ans: 24
Question
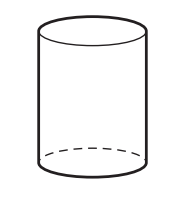
Irina has some solid building blocks.
(a) Write down the mathematical name of this solid.
Answer/Explanation
Ans: Cylinder
(b) Irina describes the shape of a different block.
She says:
It has 12 edges and 8 vertices. All the faces are the same shape.
Write down the mathematical name of this solid.
Answer/Explanation
Ans: Cube or cuboid
(c) The diagram shows the end face of another block.
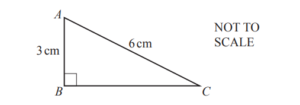
(i) Show that BC = 5.2 cm, correct to 1 decimal place.
Answer/Explanation
Ans: \(\sqrt{6^{2}-3^{2}}\)
5.19…
(ii) Find the area of triangle ABC.
Answer/Explanation
Ans: 7.79 to 7.8
(iii) This block is a triangular prism with length 8cm.
Calculate the volume of the block.
Answer/Explanation
Ans: 62.4
(d) The diagram shows another building block.
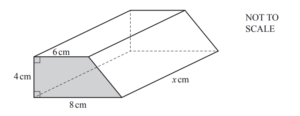
(i) Calculate the area of the end face of this block.
Answer/Explanation
Ans: 28
(ii) The volume of this block is 336 cm3.
Find the value of x.
Answer/Explanation
Ans: 12
Question
The diagram shows a point P, a shape S and lines A and B on a \(1cm^{2}\) grid.
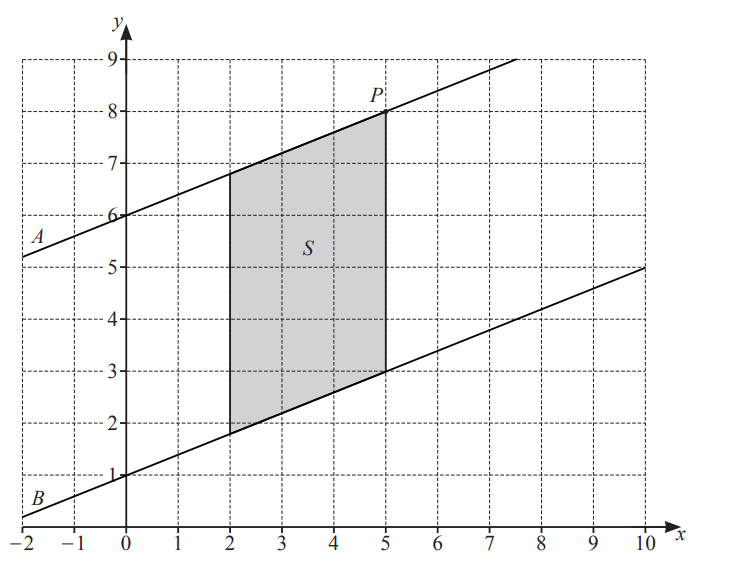
(a) Line A is parallel to line B.
Explain what parallel means.
…………………………………………………………………………………………………………………………………..
(b) Write down the coordinates of point P.
( ………………….. , ………………….)
(c) (i) Write down the mathematical name for shape S.
………………………………………….
(ii) Work out the area of shape S.
…………………………………..\( cm^{2}\)
(d) (i) Find the gradient of line A.
………………………………………….
(ii) Write down the equation of line A.
………………………………………….
Answer/Explanation
(a) Correct explanation
(b) (5,8)
(c)(i) Parallelogram
(ii)15
d(i)\(\frac{2}{5}\)
(ii)\(y=\frac{2}{5}x+6\)
Question
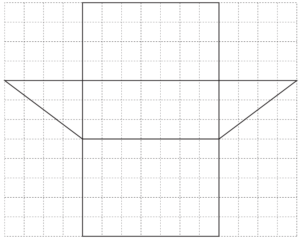
The shape above is the net of a solid drawn on a 1 cm square grid.
(a) Write down the geometrical name of the solid
(b) Find the perimeter of the net.
(c) Work out
(i) the area of one of the triangles,
(ii) the volume of the solid.
(d) A cuboid of length 4 cm and width 3 cm has the same volume as the solid.
Calculate the height of the cuboid.
Answer/Explanation
(a) Triangular prism
(b) 50.4
(c)(i) Area =\(\frac{1}{2}\times 4 \times 3\)
=6
(ii) Volume= \(Area\times 7\)
= 6.7
=42 \({cm}^3\)
(d) Given:
Volume of solid= 42\({cm}^3\)
Volume of Cuboid= l.b.h
where, l is length
b is breadth
and h is height
A/Q
Volume of solid= Volume of cuboid
42= l.b.h
42=4.3.h
\(h=\frac{42}{12}\)
h= 3.5 cm
Question
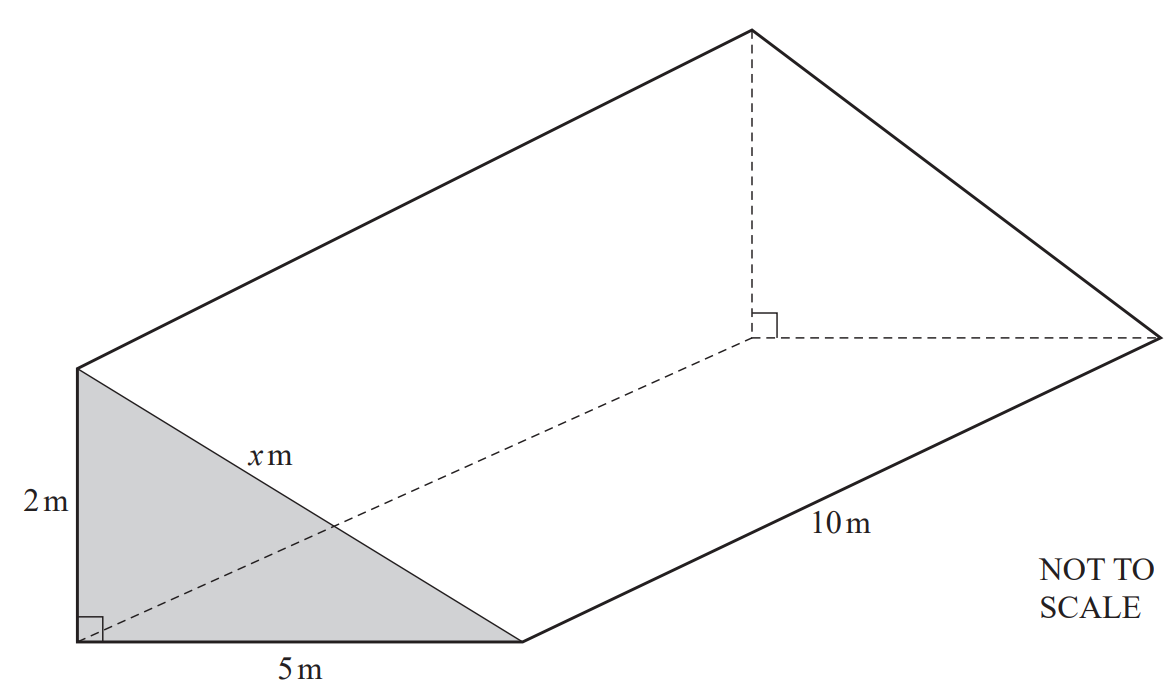
The diagram shows a ramp in the form of a triangular prism.
The cross-section is a right-angled triangle of length 5m and height 2m.
(a) Find the value of x.
Give your answer correct to 1 decimal place.
(b) Find the area of the cross-section.
(c) The ramp is 10m long.
Calculate the volume of the ramp.
(d) Calculate the total surface area of all five faces of the ramp.
(e) Each face of the ramp is painted.
Paint costs \(\$2.25\) per square metre.
Calculate the total cost of the paint.
Answer/Explanation
(a) By Pythagoras theorem,
\(x^2=2^2+5^2\)
\(x=\sqrt{4+25}\)
= \sqrt{29}\)
=5.4
(b) Area of cross section :
Area of the highlighted triangle:
\(\frac{1}{2}\times 5 \times 2\)
\(5 m^2\)
(c) Volume of ramp = Area of cross- section\(\times\) Length of ramp
= \(5 \times 10\)
= \(50 m^3\)
(d) Total surface area = Surface of 2 triangles + Area of rectangle[ABCD, AEFB, EFCD]
=\(2\times \frac{1}{2} \times 5\times 2 + 10\times 5.4 + 2\times 10 +10 \times 5\)
=134 \(m^2\)
(e) 1 \(m^2\) paint cost = \(\$2.25\)
Therefore, 134\(m^2\)= (2.25)(134)
= 301.5
Question
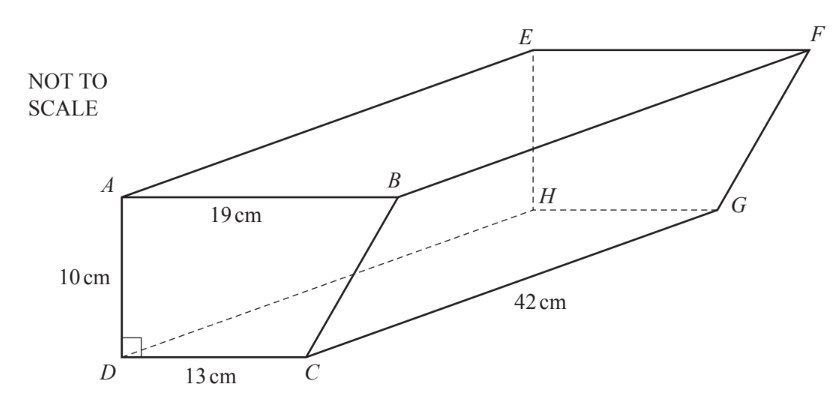
The diagram shows a block of stone in the shape of a prism of length $42 \mathrm{~cm}$. The cross-section is a trapezium $A B C D$. $A B=19 \mathrm{~cm}, A D=10 \mathrm{~cm}, D C=13 \mathrm{~cm}$ and angle $A D C=90^{\circ}$.
(a) Calculate
(i) the perimeter of the rectangular face $A B F E$,
(ii) the area of the cross-section ABCD,
(iii) the volume of the block of stone.
(b) The mass of 1 cubic centimetre of the stone is 4 grams. Calculate the mass of the block. Give your answer in kilograms.
▶️Answer/Explanation
(a) (i) 122
(ii) 160
(iii) 6720 or their (a)(ii) × 42 evaluated
(b) 26.88 or their (a)(iii) × 0.004 evaluated or 26.9
Question
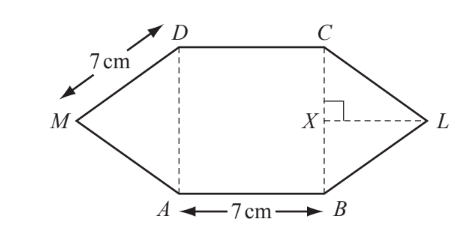
In the diagram, ABCD is a square of side 7 cm. BLC and DMA are equilateral triangles.
(a) Find the perimeter of the shape ABLCDM.
(b) (i) Write down the size of angle CBL.
(ii) Calculate the length of LX.
(c) (i) Calculate the area of triangle BLC.
(ii) Calculate the area of the shape ABLCDM.
▶️Answer/Explanation
(a) 42
(b) (i) $60^{\circ}$
(ii) $6.06(217 \ldots)$
(c) (i) 21.2 to $21.4 \mathrm{ft}$
(ii) 91.4 to $91.7 \mathrm{ft}$
Question
(a) Write down the name of a polygon with 8 sides.
(b) Find the size of the interior angle of a regular polygon with 8 sides.
(c) A regular 8-sided polygon, centre O, and side 8 cm, is shown below. M is the mid-point of the side AB.
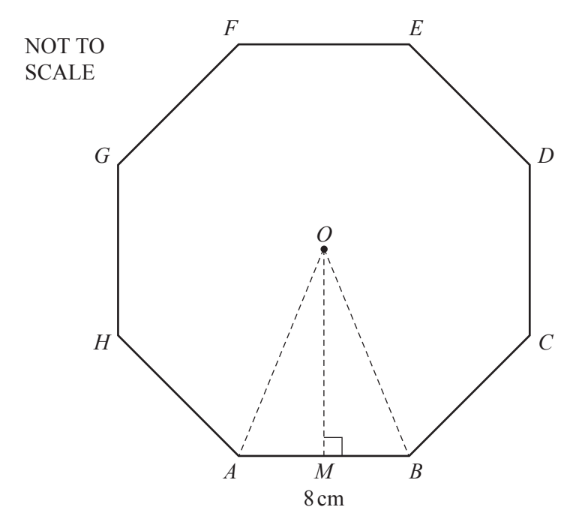
(i) Show that OM = 9.66 cm correct to 3 significant figures.
(ii) Calculate the area of the triangle AOB.
(iii) Calculate the area of the polygon.
(d) The polygon forms the cross-section of a box. The box is a prism of height 12 cm. Calculate the volume of the box.
(e) The box contains 200 toffees in the shape of cuboids, 3 cm by 2 cm by 2 cm. Calculate
(i) the total volume of the 200 toffees,
(ii) the percentage of the volume of the box not filled by the toffees.
▶️Answer/Explanation
(a) Octagon
(b) 135
(c) (i) Angle $O A B=$ their (b) $/ 2$ or angle $A O M=90$ – their $(\mathbf{b}) / 2$ $9.656 \ldots$ or 9.66
(ii) 38.6 to 38.64
(iii) 308.8 to 309.12
(d) 3705.6 to 3709.44 or 3710
(e) (i) 2400
(ii) $35.2(3 \ldots)$ to $35.3(0 \ldots)$
Question
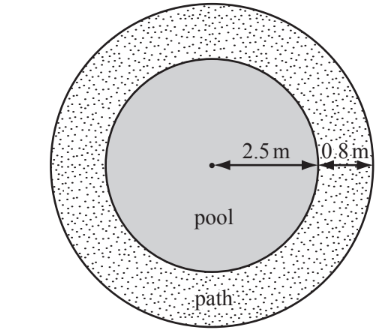
The diagram shows a circular pool, of radius 2.5 metres, surrounded by a path 0.8 metres wide.
(a) Calculate
(i) the perimeter of the pool,
(ii) the area of the pool,
(iii) the area of the path.
(b) The water in the pool has a depth of 0.4 metres. Calculate the volume of water in the pool. Give your answer in litres. [1 cubic metre = 1000 litres.]
(c) When the pool is emptied for cleaning, the water flows out at a rate of 250 litres each minute. Calculate how long it takes to empty the pool. Give your answer to the nearest minute.
▶️Answer/Explanation
(a) (i) 15.7 art
(ii) 19.6 art
(iii) 14.6 art
(b) Within range 7840 to 7860
(c) 31
