iGCSE Mathematics (0580) :C6.1 Interpret and use three-figure bearings. iGCSE Style Questions Paper 1

Question

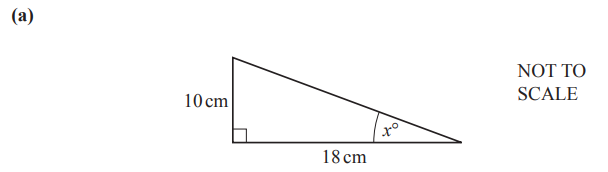
Calculate the value of $ x $.

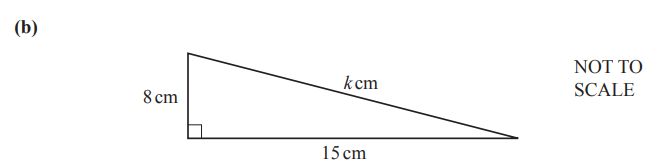
Trigonometry problem for k

Calculate the value of $ k $.

▶️ Answer/Explanation

Answers:

(a) $ x = 29.1 $ (or 29.05…)

(b) $ k = 17 $

Explanation:

(a) Finding $ x $:

Given a right-angled triangle with:
- Adjacent side to angle $ 47^\circ = 20 $ cm
- Hypotenuse $ = x $ cm
Use the cosine ratio:
$ \cos(47^\circ) = \frac{\text{Adjacent}}{\text{Hypotenuse}} = \frac{20}{x} $
Solve for $ x $:
$ x = \frac{20}{\cos(47^\circ)} \approx \frac{20}{0.682} \approx 29.3 \, \text{cm} $
(Note: More precise calculation gives $ x \approx 29.05 $)

(b) Finding $ k $:

Given a right-angled triangle with:
- Opposite side to angle $ 30^\circ = k $ cm
- Adjacent side $ = 30 $ cm
Use the tangent ratio:
$ \tan(30^\circ) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{k}{30} $
Solve for $ k $:
$ k = 30 \times \tan(30^\circ) = 30 \times 0.577 \approx 17.32 $
(Exact value: $ k = 30 \times \frac{1}{\sqrt{3}} \approx 17.32 $, but likely rounded to $ 17 $)

Question

The diagram shows a flagpole, $BD$, held by two ropes, $AD$ and $CD$.

$ABC$ is a straight line and angle $\angle ABD = 90^\circ$.

$AD = 21.2 \, \text{m}, \, AB = 16.5 \, \text{m}, \, \text{and angle } \angle BCD = 48^\circ.$

(a) Show that the height of the flagpole $BD$ is $13.3 \, \text{m}$, correct to 1 decimal place.

(b) Calculate the length of the rope $CD$.

▶️ Answer/Explanation

Solution

(a) Ans: 13.3 m

Using Pythagoras’ Theorem in $\triangle ABD$:

$AD^2 = AB^2 + BD^2 \Rightarrow BD = \sqrt{21.2^2 – 16.5^2} = \sqrt{177.19} \approx 13.31 \, \text{m}$.

Rounded to 1 decimal place, $BD = 13.3 \, \text{m}$.

(b) Ans: 17.9 m

Using the sine ratio in $\triangle BCD$:

$\sin(48^\circ) = \frac{BD}{CD} \Rightarrow CD = \frac{13.3}{\sin(48^\circ)} \approx 17.9 \, \text{m}$.

Resources