Question
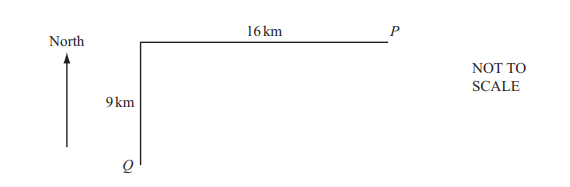
The diagram shows the route of a ship that leaves a port, P.
It travels due west for 16km and then changes course to due south for 9km.
(a) Calculate the straight line distance PQ.
Answer/Explanation
Ans: 18.4
(b) Use trigonometry to calculate the bearing of P from Q.
Answer/Explanation
Ans: [0]60.4 to [0]60.73
Question
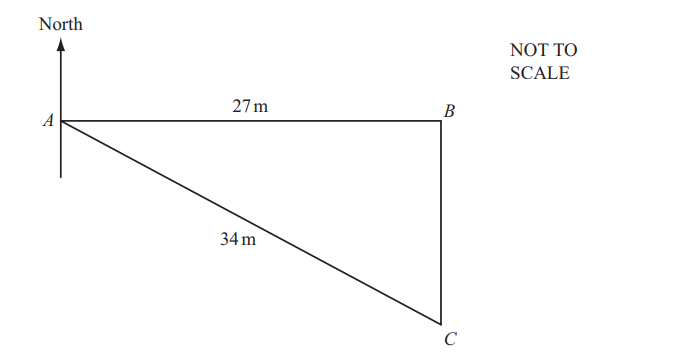
In the diagram, B is 27 metres due east of A.
C is 34 metres from A and due south of B.
(a) Using trigonometry, calculate angle ACB.
Answer/Explanation
Ans: 52.6
(b) Find the bearing of C from A.
Answer/Explanation
Ans: 127 or 127.4[…]
Question
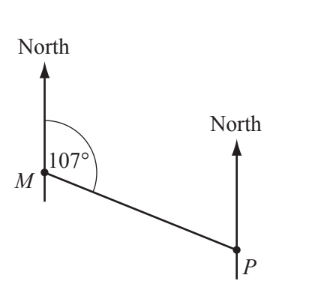
The bearing of P from M is 107°. Work out the bearing of M from P.
▶️Answer/Explanation
If the bearing of P from M is 107°, then the bearing of M from P will be the opposite direction, which is 180° added to 107°:
Bearing of M from P = 180° + 107°
Calculating this, we have:
Bearing of M from P = 287°
Therefore, the bearing of M from P is 287°.
Question
A and B are two points marked on a map. By measuring a suitable angle, find the bearing of A from B.
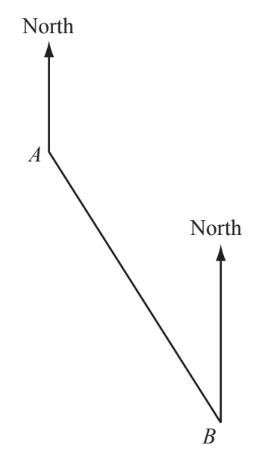
▶️Answer/Explanation
$328 \pm 2$ (ie 326 to 330$)$
