Question
(a) The diagram shows the position of town A and town B, on a map.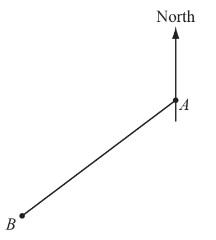
(i) Measure the length, in millimetres, of the line AB.
(ii) Measure the bearing of town B from town A.
(b) A triangular fi eld has sides of length 550m, 300m and 400m.
(i) Construct the triangle, using a ruler and compasses only.
Use a scale of 1 cm to represent 50m.
The side of length 550m has been drawn for you.![]()
(ii) By making a suitable measurement on your diagram, calculate the area of the fi eld.
Give your answer in square metres.
Answer/Explanation
Answer:
(a) (i) 44 – 46
(ii) 231 – 235
(b) (i) Fully correct drawing with arcs
52250 to 60500 nfww
Question
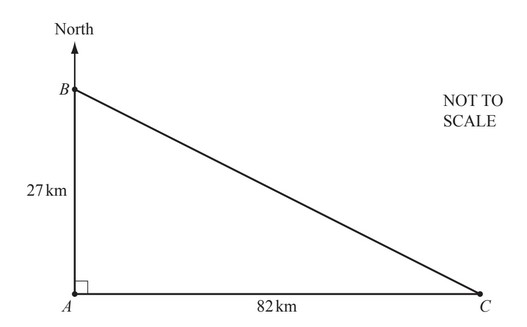
The diagram shows the positions of three towns A, B and C.
B is 27km north of A and the distance between A and C is 82km.
(a) Calculate BC.
(b) Write down the three fi gure bearing of C from A.
(c) (i) Use trigonometry to calculate angle ABC.
(ii) Work out the bearing of C from B.
(d) (i) Calculate the area of triangle ABC.
(ii) The land forming the triangle ABC is valued at $8400 for each square kilometre.
Calculate the value of this land.
Answer/Explanation
Answer:
(a) 86.3 or 86.33075…..
(b) 090 cao
(c) (i) 71.8 or 71.77492…..
(ii) 108.2 or 108
(d) (i) 1107
(ii) 9 298 800
Question
The scale drawing represents the positions of 3 towns, A, B and C.
The scale is 1 centimetre represents 4 kilometres.
(a) Measure the bearing of B from A.
Answer/Explanation
Ans: 106 to 110
(b) A transmitter is placed near to the 3 towns.
(i) The transmitter is equidistant from A and B.
Using a straight edge and compasses only, construct the locus of points equidistant from A and B.
Answer/Explanation
Ans: Correct bisector of AB constructed with 2 pairs of arcs.
(ii) The transmitter is also on the bisector of angle ABC.
Using a straight edge and compasses only, construct the bisector of angle ABC.
Answer/Explanation
Ans: Correct bisector of angle ABC with arcs
(iii) Mark the position, T, of the transmitter on the scale drawing.
Answer/Explanation
Ans: T marked at intersection of their bisectors
(c) Work out the actual distance, in kilometres, of town A from T.
Answer/Explanation
Ans: 24.4[km] to 26.0[km]
(d) The signal from the transmitter has a range of 30 kilometres in all directions.
On the scale drawing, construct the locus of points 30 kilometres from T.
Answer/Explanation
Ans: Circle, radius 7.5(±0.2)cm centre T.
(e) Would the signal from the transmitter reach town C ?
Give a reason for your answer.
Answer/Explanation
Ans: No It is outside the circle. oe
Question
The scale drawing shows two villages, A and B, joined by a straight road.
The scale is 2 centimetres represents 1 kilometre.
Scale: 2cm to 1km
(a) (i) Work out the distance, in kilometres, from A to B.
Answer/Explanation
Ans: 4.8
(ii) Measure the bearing of B from A.
Answer/Explanation
Ans: 137
(b) Another village, C, is 3.2 km from A on a bearing of 310°.
Mark and label the position of C on the diagram.
Answer/Explanation
Ans: Correct length and bearing
(c) In this part use a straight edge and compasses only and show your construction arcs clearly.
Construct the perpendicular bisector of AB.
Answer/Explanation
Ans: Perpendicular bisector with 2 sets of correct arcs
(d) A school is
• closer to village A than to village B
and
• less than 3 kilometres from village B.
On the diagram, shade the region in which the school must be.
Answer/Explanation
Ans: Correct area shaded
(e) Nelson cycles from village B to the nearest town.
He cycles a total distance of 12km at an average speed of 15km/h.
He leaves village B at 1015.
Work out the time he arrives at the nearest town.
Answer/Explanation
Ans: 11 03
Question
The Patel family flies from their home town, H, to Kiruna, K, in Lapland.
(a) The scale drawing shows their journey.
The scale is 1 centimetre represents 40 kilometres.
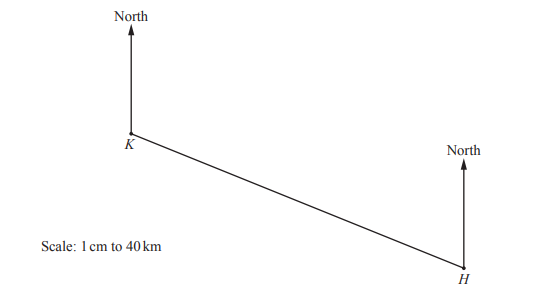
(i) Measure the bearing of K from H.
Answer/Explanation
Ans: 292
(ii) Work out the distance in kilometres from H to K.
Answer/Explanation
Ans: 380 km
(iii) The average speed of the plane is 450km/h.
Find the average speed in m/s.
Answer/Explanation
Ans: 125 m/s
(b) The probability that the plane arrives on time is 0.15 .
(i) Write down the probability that the plane does not arrive on time.
Answer/Explanation
Ans: 0.85
(ii) Every year there are 240 flights from H to K.
Calculate the expected number of flights that arrive on time.
Answer/Explanation
Ans: 36
(c) The Patel family has six suitcases.
The number of items in each suitcase is shown below.
15 16 16 18 19 21
(i) Find the range.
Answer/Explanation
Ans: 6
(ii) Write down the mode.
Answer/Explanation
Ans: 16
(iii) Work out the median.
Answer/Explanation
Ans: 17
(iv) Calculate the mean.
Answer/Explanation
Ans: 17.5
(v) Find the probability that a suitcase chosen at random has more than 18 items.
Answer/Explanation
Ans: \(\frac{2}{6}oe\)
(d) Mr Patel buys a bag of sweets.
The bag of sweets costs $3.25 .
(i) Calculate the cost of the sweets in euros (€) when the exchange rate is €1 = $1.24 .
Answer/Explanation
Ans: 2.62
(ii) The weight, w grams, of the bag of sweets is 250g correct to the nearest 10 g.
Complete this statement about the value of w.
Answer/Explanation
Ans: 245 ≤ w < 255
Question
The diagram shows the positions of two villages Dormouth, D, and Greenton, G.
The scale is 1 centimetre represents 20 kilometres.
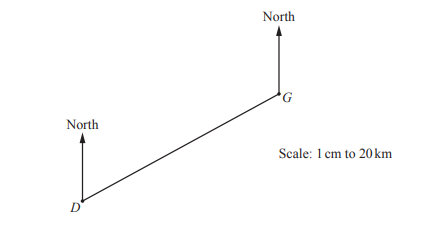
(a) Find the distance, in kilometres, from Dormouth to Greenton.
Answer/Explanation
Ans: 126
(b) Measure the bearing of Dormouth from Greenton.
Answer/Explanation
Ans: 240
(c) Foxhill is 84 km from Dormouth.
The bearing of Foxhill from Dormouth is 105°.
Mark the position of Foxhill on the diagram. Label it F.
Answer/Explanation
Ans:Correct position on diagram
(d) A straight road joins Dormouth to Foxhill.
A car drives from Dormouth to Foxhill at a constant speed of 54km/h.
Calculate the time it takes to complete the 84km journey.
Give your answer to the nearest minute.
Answer/Explanation
Ans: 1 hour and 33 min
(e) Change 54 km/h to m/s .
Answer/Explanation
Ans: 15
Question
The scale drawing shows the positions of two towns, X and Y.
The scale is 1 centimetre represents 5 kilometres.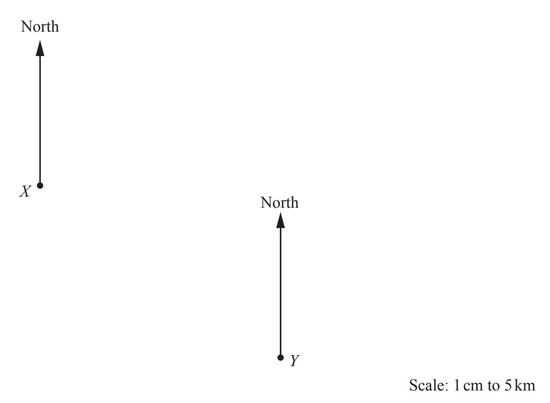
(a) Work out the actual distance from town X to town Y.
…………………………………… km
(b) Measure the bearing of town X from town Y.
(c) An airport, A, is 22.5km from town Y on a bearing of 050°.
Mark and label the position of A on the scale drawing.
Answer/Explanation
Answer:
(a) 35
(b) 305
(c) Point marked in correct position
Question
(a) The scale drawing shows port A and port B.
The scale is 1 centimetre represents 15 kilometres.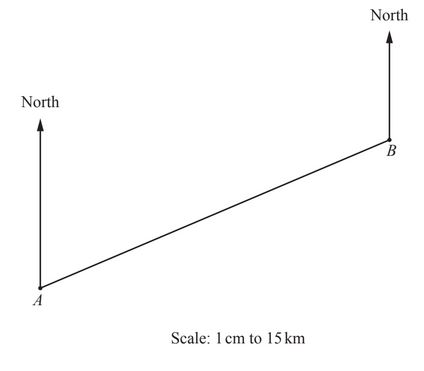
A ship sails from port A to port B.
(i) Measure the bearing of port B from port A.
(ii) Find the actual distance from port A to port B.
………………………… km
(iii) The ship then sails from port B to port C.
Port C is 90km from port B on a bearing of 146°.
On the scale drawing mark the position of port C.
(b) Another ship sails from port P to port Q.
It then sails from port Q to port R before returning to port P.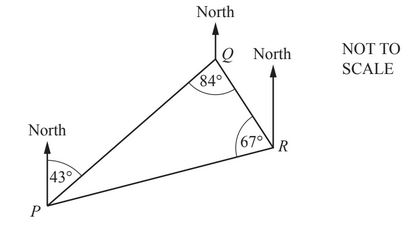
(i) Find angle RPQ.
Angle RPQ = ………………………………………….
(ii) Find the bearing of port P from port R.
(c)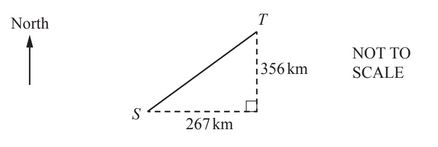
Port T is 267 km east and 356km north of port S.
Calculate the distance ST.
ST = …………………………………….. km
Answer/Explanation
Answer:
(a) (i) [0]67
(ii) 135
(iii) Correct diagram
(b) (i) 29
(ii) 252
(c) 445
Question
Burton City is a football team.
(a) Burton City has 1732 supporters who want to travel to the next game.
The football club hires some buses.
Each bus seats 52 supporters.
(i) Work out the number of buses needed to take these supporters to the game.
(ii) The cost of the buses will be shared equally amongst these supporters.
Each bus costs $198 to hire.
Work out the amount that each supporter must pay.
Give your answer correct to the nearest 10 cents.
$ ……………………..
(b) Adam and Mabel are two supporters.
The scale drawing shows the positions of Adam’s home, A, and Mabel’s home, M.
The scale is 1 centimetre represents 500 metres.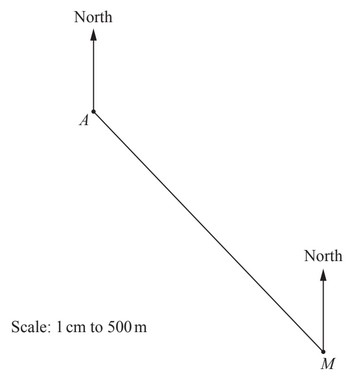
(i) Work out the distance in kilometres from A to M.
…………………………………….. km
(ii) Burton City’s football ground is on a bearing of 105° from A and on a bearing of 068° from M.
Mark the position of the football ground on the scale drawing.
(c) Teams are given points for winning or drawing games.
A win is given w points and a draw is given d points.
No points are given when the team loses.
(i) Burton City has 24 points after winning 2 games and drawing 5 games.
Complete the equation.
2w + 5d = ………………..
(ii) Sowton Rovers is another football team.
Sowton Rovers has 29 points after winning 3 games and drawing 4 games.
Write this information as an equation.
………………………………….. = ………………………..
(iii) Solve your two equations to find the number of points for a win and the number of points for a draw.
You must show all your working.
w = ………………………………………….
d = ………………………………………….
(iv) Another team, Cranbrook United, has played 12 games.
It has won 4 games, drawn 5 games and lost 3 games.
Work out the number of points Cranbrook United has after 12 games.
Answer/Explanation
Ans:
(a) (i) 34
(ii) 3.90
(b) (i) 3.9
(ii) football ground indicated in
correct position
(c) (i) 24
(ii) 3w + 4d = 29
(iii) [w] 7
[d] 2
(iv) 38
Question
The scale drawing shows the positions of three towns A, B and C.
The scale is 1 centimetre represents 12 kilometres.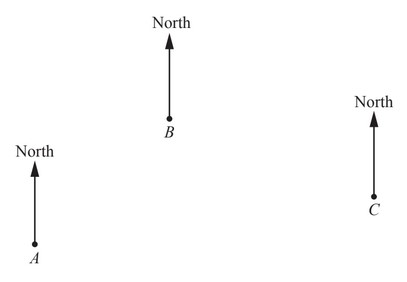
Scale: 1 cm to 12km
(a) Find the actual distance between town A and town B.
……………………………………. km
(b) Measure the bearing of town B from town A.
(c) Measure the bearing of town B from town C.
(d) Town D is 84 km from town A and 42km from town C.
(i) In this part, use a ruler and compasses only and show your construction arcs.
On the diagram, construct a possible position for town D.
(ii) A plane takes 10 minutes to fly the 84km from town A to town D.
Work out the average speed of the plane in kilometres per hour.
…………………………………. km/h
(e) The bearing of town E from town A is 118°.
Work out the bearing of town A from town E.
Answer/Explanation
Ans:
(a) 54.6
(b) [0]47
(c) 292
(d)(i) Arc centre A radius 7 cm
Arc centre C radius 3.5 cm
One point marked at intersection
of correct arcs
(ii) 504
(e) 298
Question
The scale drawing shows the positions of Bogota (B) and Quito (Q).
The scale is 1 centimetre represents 150 kilometres.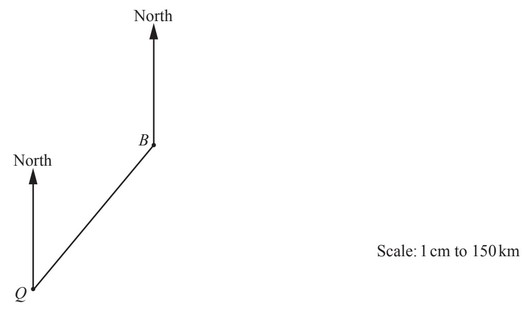
(a) (i) Measure the length of the line BQ.
…………………………………… cm
(ii) Work out the actual distance from Bogota to Quito.
…………………………………… km
(iii) Measure the bearing of Quito from Bogota.
(b) A plane leaves Quito and flies straight to Manaus.
Manaus is 2100 km on a bearing of 100° from Quito.
On the scale drawing, mark the position of Manaus (M).
(c) The plane flies the 2100km from Quito to Manaus at an average speed of 550km/h.
Calculate the time taken for this flight
(i) in hours, correct to 3 significant figures,
…………… h
(ii) in hours and minutes, correct to the nearest minute.
…………………… h …………………… min
Answer/Explanation
Answer:
(a) (i) 4.4
(ii) 660
(iii) 220
(b) 14 [cm] from Q
100° from Q
(c) (i) 3.82 cao
(ii) 3[h] 49[min]
Question
(a) Complete this statement.
To be obtuse, an angle must be between ………………………….. degrees and ……………………… degrees.
(b) 
Choose one word from the box to complete each statement.
A ………………………has no lines of symmetry but has rotational symmetry of order 2.
A ……………………………..has two lines of symmetry but no right angles.
A …………………………..has one line of symmetry but no rotational symmetry.
(c) 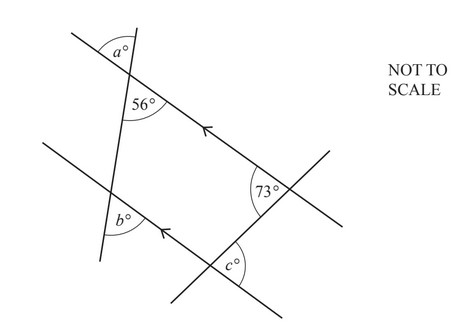
The diagram shows four straight lines.
Write down the values of a, b and c.
Give a geometrical reason for each answer.
a = ………………….because …………………………………………..
b = ………………………because …………………………………………………………………..
c = ……………….because ……………………………………………
(d) The scale drawing shows the positions of two towns F and G.
The scale is 1 cm represents 1.5km.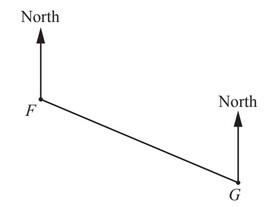
Scale: 1cm to 1.5 km
(i) Measure the bearing of G from F.
(ii) Find the distance, in kilometres, between town F and town G.
…………………. km
(iii) Another town, H, is 10.5km from town G.
The bearing of H from G is 174°.
On the scale drawing, mark the position of town H.
Answer/Explanation
Answer:
(a) 90, 180
(b) parallelogram
rhombus
kite
(c) 56 vertically opposite [to \(56^o\)]
56 corresponding [to \(56^o\)]
73 alternate [ to \(73^o\)]
(d) (i) 113
(ii) 7.5 km
(ii) H correct
Question
(a) The scale drawing shows the positions of a lighthouse L and a ship S.
The scale is 1 centimetre represents 5 kilometres.
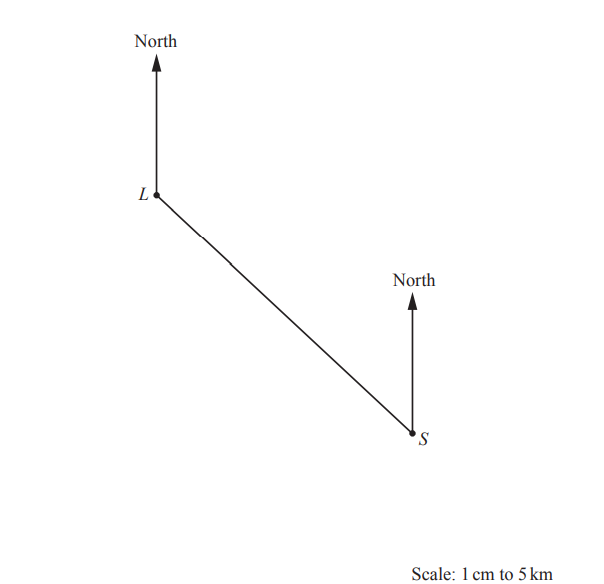
(i) Work out the actual distance, in kilometres, from S to L.
…………………………………… km
(ii) Measure the bearing of S from L.
………………………………………….
(iii) Another ship, T, is 22km from L on a bearing of 210°.
Mark and label the position of T on the scale drawing.
(b) In this part, use a ruler and compasses only and show your construction arcs clearly.
The scale drawing shows the positions of two yachts, P and Q.
The scale is 1 centimetre represents 100 metres.

(i) Construct the locus of points equidistant from P and Q. [2]
(ii) Another yacht, Y, is
• closer to P than to Q
and
• less than 700m from Q.
On the scale drawing, construct and shade the region where yacht Y is.
Answer/Explanation
(a)(i) 37
(ii) 133
(iii) T plotted correctly
(b)(i) Correct perpendicular bisector of PQ
(ii) Arc centre Q, radius 7 cm
Correct region shaded
Question
The scale drawing shows the positions of Annika’s house, A, and Bernhard’s house, B, on a map.
The scale is 1 centimetre represents 300 metres.
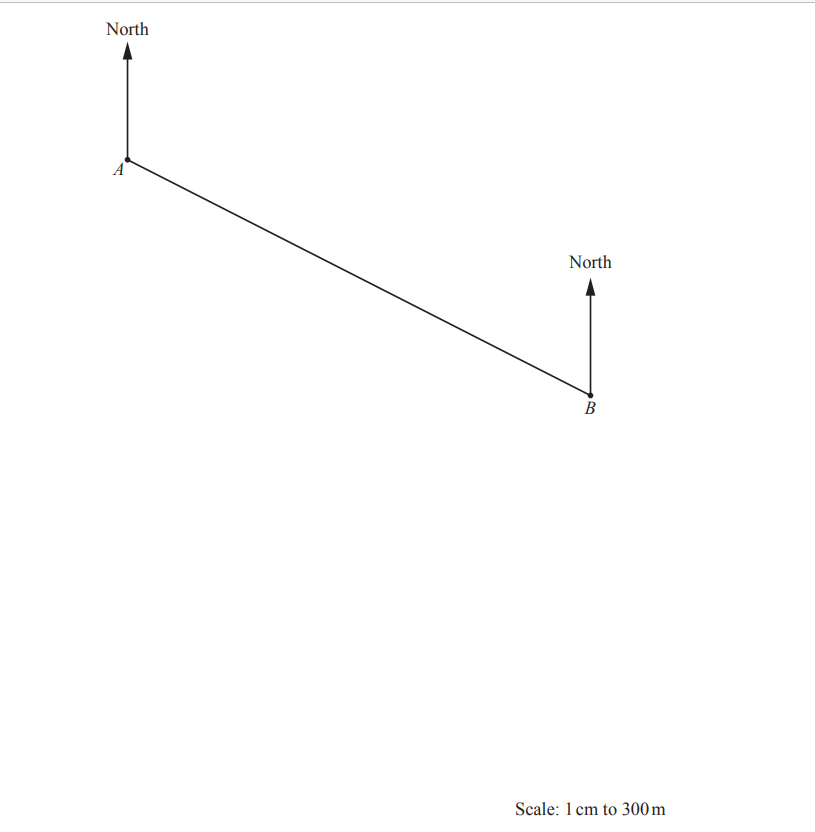
(a) Work out the actual distance, in metres, between Annika’s house and Bernhard’s house.
…………………………………….. m
(b) Measure the bearing of Bernhard’s house from Annika’s house.
…………………………………………
(c) (i) Using a straight edge and compasses only, construct the perpendicular bisector of AB.
Show all your construction arcs.
(ii) Cordelia’s house is
• the same distance from Annika’s house and Bernhard’s house
and
• due south of Annika’s house.
Mark on the map the position of Cordelia’s house.
Label this point C.
(d) Dougie’s house is
• on a bearing of 320° from Bernhard’s house
and
• 1650m from Annika’s house.
Mark on the map the two possible positions of Dougie’s house.
Label each of these points D.
Answer/Explanation
(a) 3300
(b) 117
(c)(i) Correct ruled perpendicular bisector
with 2 pairs of arcs
(ii) C marked correctly
(d) D marked correctly twice with correct arc(s) and line seen
Question
Triangles A, B and C are shown on the grid.
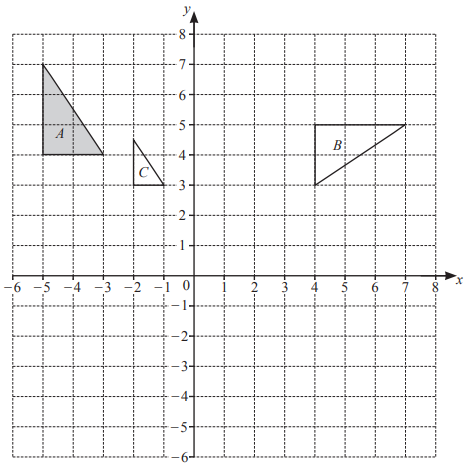
(a) Describe fully the single transformation that maps
(i) triangle A onto triangle B, [3]
(ii) triangle A onto triangle C.[3]
(b) On the grid,
(i) translate triangle A by the vector \(\binom{6}{-2},\) [2]
(ii) reflect triangle A in the line y = 1. [2]
Answer/Explanation
Ans:
5(a)(i) Rotation
90° clockwise oe
[center] (0, 0) oe
5(a)(ii) Enlargement
[sf] 0.5 oe
[center] (1, 2)
5(b)(i) Triangle at (3, 2) (1, 5) (1, 2)
5(b)(ii) Triangle at (–3, –2) (–5, –2) (–5, –5)
Question
(a) The scale drawing shows the positions of two towns, Yatterford (Y) and Rexley (R), on a map.
The scale is 1 centimetre represents 15 kilometres.
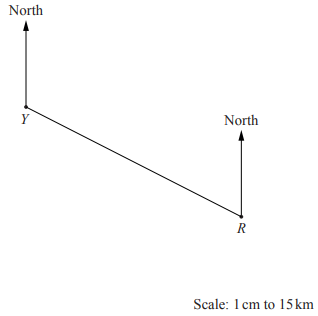
(i) Write the scale of the map in the form 1: n.
1 : ……………………………………….
(ii) Work out the actual distance of Rexley from Yatterford.
…………………………………… km
(iii) Measure the bearing of Rexley from Yatterford.
…………………………………………
(iv) A hospital is to be built on an area of land between 45km and 60km from Yatterford.
The bearing of the hospital from Yatterford is between 250° and 295°.
On the map, construct and shade the region in which the hospital is to be built.
(b) The bearing of Bartown from Whitestoke is 073°.
Work out the bearing of Whitestoke from Bartown.
…………………………………………
Answer/Explanation
(a)(i)[1:] 1500 000
(ii)96
(iii)117
(iv)Correct region shaded
(b)253
Question
The scale drawing shows the positions of an airport (A) and a train station (T) on a map.
The scale is 1 centimeter represents 2 kilometers.
Scale: 1cm to 2km
(a) Work out the actual distance, in kilometers, of the train station from the airport.
km [2]
(b) Measure the bearing of the airport from the train station.[1]
(c) There is a straight road that is equidistant from T and A.
Using a straight edge and compasses only, construct the position of the road on the map. Show all your construction arcs. [2]
(d) Krishna’s house is
- on a bearing of 203° from the airport
and
- 8.8km from the train station.
On the map, mark the two possible positions of Krishna’s house.
Label each of these points K. [4]
(e) The bus station is not shown on the map.
The bearing of the bus station from the train station is 318°.
Work out the bearing of the train station from the bus station.[2]
Answer/Explanation
Ans:
7(a) 19.2
7(b) [0]45
7(c) Correct ruled perpendicular bisector with 2 pairs of arcs
7(d) K marked correctly twice
7(e) 138
Question
Point B is 36km from point A on a bearing of 140°.
(a) Using a scale of 1 centimetre to represent 4 kilometres, mark the position of B.

(b) (i) Point C is 28 km from A and 20km from B.
The bearing of C from A is less than 140°.
Using a ruler and compasses only, construct triangle ABC.
Show all your construction arcs.
(ii) Measure angle ACB.
Angle ACB = …………………………………………..
Answer/Explanation
(a) Correct position of town B
(b)(i) Correct triangle drawn
(ii) 38 to 42
Question
(a) The scale drawing shows the positions of a rock, R, and a statue, S, on a map.
The scale is 1 centimetre represents 6 metres.
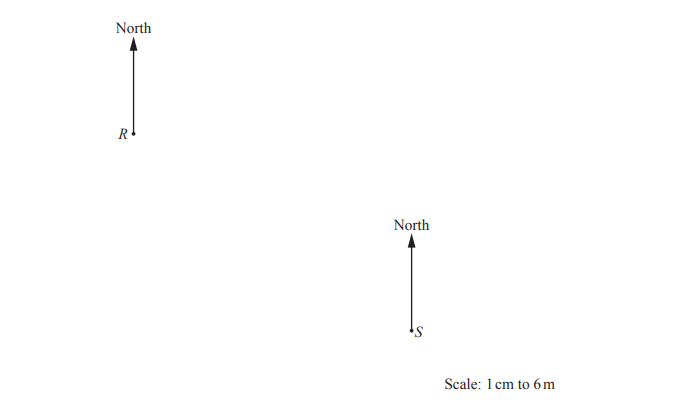
(i) Work out the actual distance between R and S.
……………………………………… m
(ii) A flagpole, F, is on a bearing of 164° from S.
Work out the bearing of S from F.
………………………………………….
(iii) Ishaan uses the map to find some treasure, T.
T is on a bearing of 076° from R and on a bearing of 337° from S.
Mark the position of T on the map.
(b) The treasure is a bag of coins.
The coins are made from three different metals.
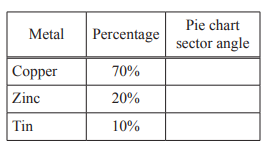
(i) Complete the table.
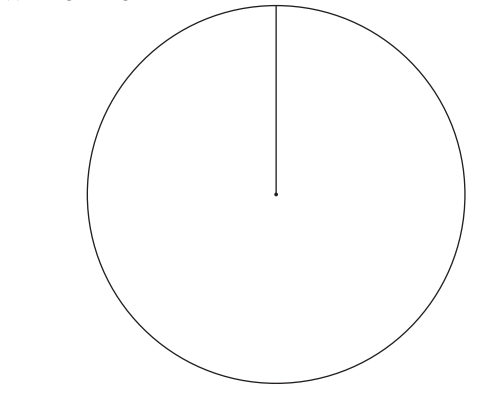
(ii) Complete the pie chart.
Answer/Explanation
(a))(i) 54
(ii) 344
(iii) T marked correctly
(b)(i) 252, 72, 36
(ii) Correct pie chart drawn
Question
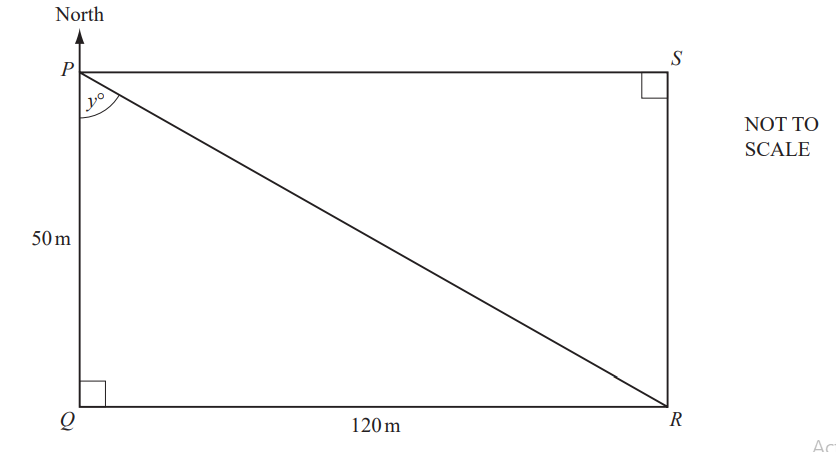
The diagram shows a rectangular field, PQRS.
QR = 120m, PQ = 50m and P is due North of Q.
Bill and Said run from P to R.
Bill runs along the sides PQ and QR.
Said runs directly from P to R.
(a) Calculate how far
(i) Bill runs,
Answer/Explanation
Ans: 170
(ii) Said runs.
Answer/Explanation
Ans: 130
(b) Bill takes 34 seconds to reach R.
Calculate Bill’s average speed.
Answer/Explanation
Ans: 5
(c) Said runs at 4m/s.
Who arrives at R first and by how many seconds?
Answer/Explanation
Ans: Said by 1.5 secs
(d) (i) Use trigonometry to calculate the size of the angle marked y.
Answer/Explanation
Ans: 67.4°
(ii) Find the bearing of R from P.
Answer/Explanation
Ans: 113° or 112.6°
(e) Calculate the area of the field in square kilometres.
Give your answer in standard form.
Answer/Explanation
Ans: 6 × 10–3
Question
(a)
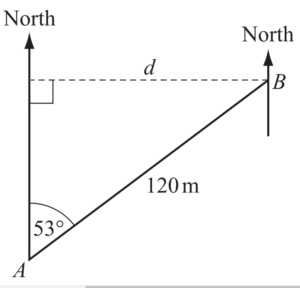
B is 120m from A on a bearing of 053°.
Calculate
(i) the distance d,
(ii) the bearing of A from B
(b)
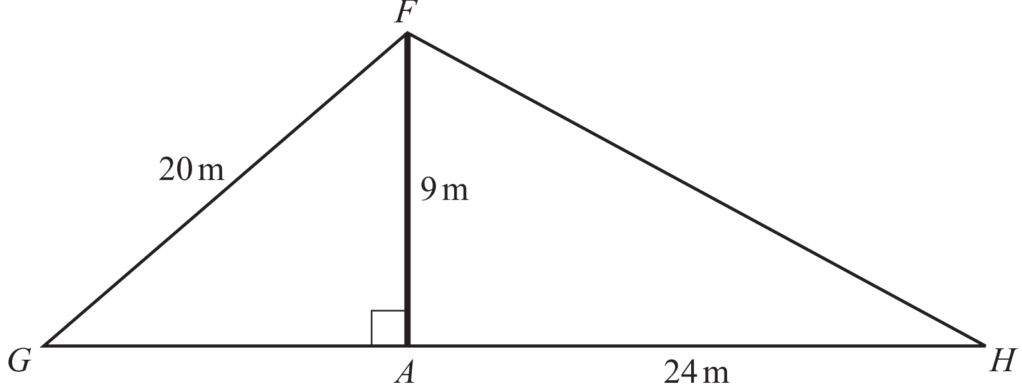
A vertical flagpole, AF, is 9m high.
It is held in place by two straight wires FG and FH.
FG = 20m and AH = 24m.
G, A and H lie in a straight line on horizontal ground.
Calculate
(i) angle FHA,
(ii) the distance GA.
Answer/Explanation
(a)(i) 90+53+\(\angle ABC\) =180
\(\angle ABC\)=180-143
\(\angle ABC\)=37
Now, d=120 Cos 37\((37)^/circ\)
=120\(\times0.7986\)
=95.84
(ii) Bearing means angle measured clockwise from north.
= 233
(b)(i) \(\angle FHA\):
FH=\(\sqrt{(24)^2+(9)^2}\)
=\(\sqrt{576+81}\)
=\(\sqrt{657}\)
= 25.63
\(tan \theta=\frac{9}{24}\)
\(\theta\) = \((\tan)^{-1}(\frac{9}{24})\)
= 20.55
(ii) Distance GA:-
\((20)^2\)=\((GA)^2+9^2\)
GA=\(\sqrt{400-81}\)
= \(\sqrt{319}\)
= 17.9
Question
(a)![]()
The line AB is drawn above.
Parts (i), (iii), and (v) must be completed using a ruler and compasses only.
All construction arcs must be clearly shown.
(i) Construct triangle ABC with AC = 7 cm and BC = 6 cm.
(ii) Measure angle BAC.
(iii) Construct the bisector of angle ABC.
(iv) The bisector of angle ABC meets AC at T.
Measure the length of AT.
(v) Construct the perpendicular bisector of the line BC.
(vi) Shade the region that is
• nearer to B than to C
and
• nearer to BC than to AB.
(b) A ship sails 40 km on a bearing of 040° from P to Q.
(i) Using a scale of 1 centimetre to represent 5 kilometers, make a scale drawing of the path of
the ship.
Mark the point Q.
(ii) At Q the ship changes direction and sails 30 km on a bearing of 160° to the point R.
Draw the path of the ship.
(iii) Find how far, in kilometres, the ship is from the starting position P.
(iv) Measure the bearing of P from R.
Answer/Explanation
(a)(i) Steps for each part of the construction:
(i) Draw a line segment AB of length 6 cm.
From point A, draw an arc with radius 7 cm.
From point B, draw an arc with radius 6 cm.
The two arcs intersect at point C. Draw a line segment BC to complete triangle ABC.
(ii) Use a protractor to measure the angle BAC.
(iii) Draw an arc with center at point B and radius greater than half the length of segment BC.
Draw another arc with the same radius, but this time with center at point C.
The two arcs intersect at point D.
Draw the line segment BD to bisect angle ABC.
(iv) Draw an arc with center at point B and radius equal to the length of segment BD.
Draw another arc with the same radius, but this time with center at point D.
The two arcs intersect at point T.
Draw the line segment AT.
(v) Draw an arc with center at point B and radius greater than half the length of segment BC.
Draw another arc with the same radius, but this time with center at point C.
The two arcs intersect at points P and Q.
Draw the line segment PQ, which is the perpendicular bisector of BC.
(vi) Shade the region that is closer to point B than to point C, and also closer to line segment BC than to line segment AB.
(ii) To draw the path of the ship from Q to R, we, need to start by locating point Q on scale . Then, draw a line segment of 6 centimeters in the direction of bearing 160degree. This line segment represents the 30 km distance that the ship traveled from Q to R. Finally, label point R at the end of the line segment to complete the drawing of the ship’s path.
Question
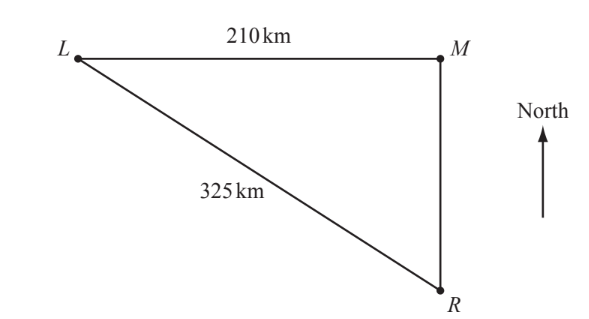
The diagram shows three islands, L, M and R.
L is due west of M and R is due south of M.
LM = 210 km and LR = 325 km.
(a) Calculate the distance RM.
(b) (i) Use trigonometry to calculate angle LRM.
(ii) Find the bearing of L from R.
(c) (i) A ferry travels directly from M to L. It leaves M at 06 15 and arrives at L at 13 45. Calculate the average speed of the ferry in kilometres per hour.
(ii) The ferry then travels the 325 km from L to R at an average speed of 37 km/h. Calculate the time taken. Give your answer in hours and minutes, to the nearest minute.
(iii) The ferry leaves L at 14 00. Use your answer to part (c)(ii) to find the time it arrives at R.
▶️Answer/Explanation
(a) $248 \mathrm{art}$
(b) (i) $40.3^{\circ} \mathrm{art}$
(ii) $319.7(5)^{\circ}$ or $320^{\circ}$
(c) (i) 28
(ii) $8 \mathrm{~h} 47 \mathrm{~min}$
(iii) 2247 or $1047 \mathrm{pm}$
