Question
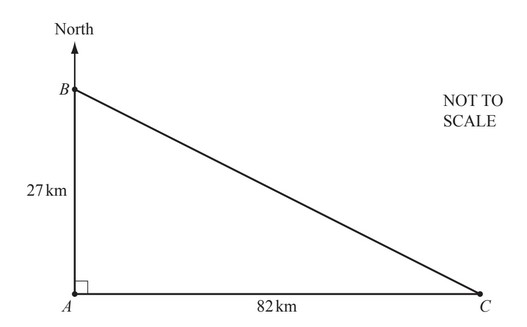
The diagram shows the positions of three towns A, B and C.
B is 27km north of A and the distance between A and C is 82km.
(a) Calculate BC.
(b) Write down the three fi gure bearing of C from A.
(c) (i) Use trigonometry to calculate angle ABC.
(ii) Work out the bearing of C from B.
(d) (i) Calculate the area of triangle ABC.
(ii) The land forming the triangle ABC is valued at $8400 for each square kilometre.
Calculate the value of this land.
Answer/Explanation
Answer:
(a) 86.3 or 86.33075…..
(b) 090 cao
(c) (i) 71.8 or 71.77492…..
(ii) 108.2 or 108
(d) (i) 1107
(ii) 9 298 800
Question
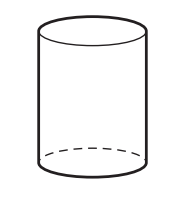
Irina has some solid building blocks.
(a) Write down the mathematical name of this solid.
Answer/Explanation
Ans: Cylinder
(b) Irina describes the shape of a different block.
She says:
It has 12 edges and 8 vertices. All the faces are the same shape.
Write down the mathematical name of this solid.
Answer/Explanation
Ans: Cube or cuboid
(c) The diagram shows the end face of another block.
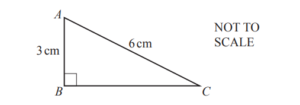
(i) Show that BC = 5.2 cm, correct to 1 decimal place.
Answer/Explanation
Ans: \(\sqrt{6^{2}-3^{2}}\)
5.19…
(ii) Find the area of triangle ABC.
Answer/Explanation
Ans: 7.79 to 7.8
(iii) This block is a triangular prism with length 8cm.
Calculate the volume of the block.
Answer/Explanation
Ans: 62.4
(d) The diagram shows another building block.
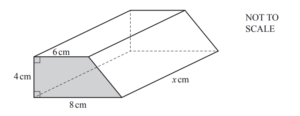
(i) Calculate the area of the end face of this block.
Answer/Explanation
Ans: 28
(ii) The volume of this block is 336 cm3.
Find the value of x.
Answer/Explanation
Ans: 12
Question
(a) 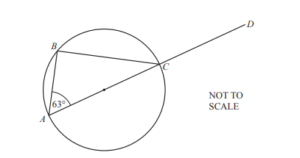
A, B and C lie on a circle with diameter AC.
AC is extended to D and angle BAC = 63°.
Work out angle BCD.
Give reasons to explain your answer.
Answer/Explanation
Ans: 153
two correct geometrical reasons.
(b) 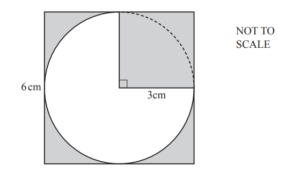
The diagram shows a circle with radius 3cm inside a square of side 6cm.
Calculate the shaded area.
Answer/Explanation
Ans: 14.8
or 14.79 to 14.80
(c) 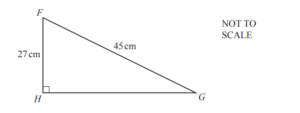
FGH is a right-angled triangle.
Calculate
(i) GH,
Answer/Explanation
Ans: 36 cm
(ii) the perimeter of the triangle,
Answer/Explanation
Ans: 108 cm
(iii) the area of the triangle.
Answer/Explanation
Ans: 486 cm2
Question
(a) The grid shows part of the net of a cuboid.
Complete the net.
Answer/Explanation
Ans: correct net drawn
(b) The volume of another cuboid is 60cm3.
Each side is a whole number of centimetres long.
Write down a possible set of dimensions for the cuboid.
Answer/Explanation
Ans:
60,1,1 or 30,2,1 or 20,3,1 or
15,4,1 or 15,2,2 or 12,5,1 or
10,6,1 or 10,3,2 or 6,5,2 or
5,4,3
(c) Each side of a cube has length 2cm.
Work out the total surface area of the cube.
Give the units of your answer.
Answer/Explanation
Ans: 24 cm2
(d) Change 9cm2 into mm2.
Answer/Explanation
Ans: 900 mm2
(e) The diagram shows a triangle.
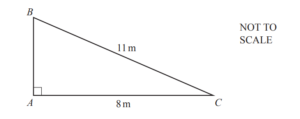
(i) Calculate the length AB.
Answer/Explanation
Ans: 7.55 or 7.549….. m
(ii) Use trigonometry to calculate angle ACB.
Answer/Explanation
Ans: 43.3 or 43.34
(f)
The diameter of the large circle is 13cm.
The radius of the small circle is 2cm.
Calculate the shaded area.
Answer/Explanation
Ans: 120 or 120.16 to 120.2 cm2
Question
Jared is building a house.
(a)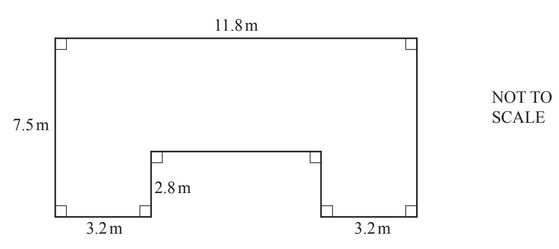
The diagram shows the plan of the floor of the house.
(i) Find the area of the floor.
……………………………………… \(m^2\)
(ii) For every square metre of floor area, it costs $2175 to build the house.
Calculate the cost of building the house.
Give your answer correct to 3 significant figures.
$…………………………………………..
(b) 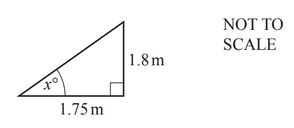
The diagram shows a section of the roof.
Using trigonometry, calculate the value of x.
x = ………………………………………….
(c) Jared invests $50000 for three years at a rate of 2% per year compound interest.
Calculate the total amount Jared receives at the end of the three years.
$ ……………………………..
(d) Jared also built an apartment for $180000.
He sells it for $198 000.
Calculate the percentage profit that he makes.
………………………. %
Answer/Explanation
Answer:
(a) (i) 73.38
(ii) 160 000
(b) 45.8 or 45.80 to 45.81
(c) 53 060.4[0]
(d) 10
Question
A, B and C are points on the circumference of a circle, centre O.
(a) Write down the mathematical name for
(i) the straight line AC,
…………………………………………
(ii) the straight line AB.
…………………………………………
(b) Give a geometrical reason why angle ABC = 90°.
………………………………………………………………………………………………………………………………………….
(c) AB = 20 cm and AC = 52cm.
(i) Use trigonometry to calculate angle BAC.
Angle BAC = ………………………………………..
(ii) Show that BC = 48cm.
(iii) Work out the area of triangle ABC.
…………………………………..\( cm^{2}\)
(iv) Work out the total shaded area.
………………………………….. \(cm^{2}\)
Answer/Explanation
(a)(i) Diameter
(ii) Chord
(b) Angle [in] semi-circle [is 90]
(c)(i) 67.4 or 67.38…..
(ii)\( (BC)^{2}=\sqrt{52^{2}-20^{2}}\)
(iii) 480
(iv) 582 or 581.8 to 582.0
Question
Triangles A, B and C are shown on the grid.
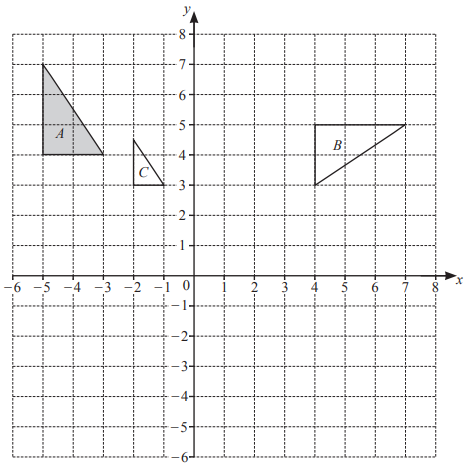
(a) Describe fully the single transformation that maps
(i) triangle A onto triangle B, [3]
(ii) triangle A onto triangle C.[3]
(b) On the grid,
(i) translate triangle A by the vector \(\binom{6}{-2},\) [2]
(ii) reflect triangle A in the line y = 1. [2]
Answer/Explanation
Ans:
5(a)(i) Rotation
90° clockwise oe
[center] (0, 0) oe
5(a)(ii) Enlargement
[sf] 0.5 oe
[center] (1, 2)
5(b)(i) Triangle at (3, 2) (1, 5) (1, 2)
5(b)(ii) Triangle at (–3, –2) (–5, –2) (–5, –5)
Question
(a)
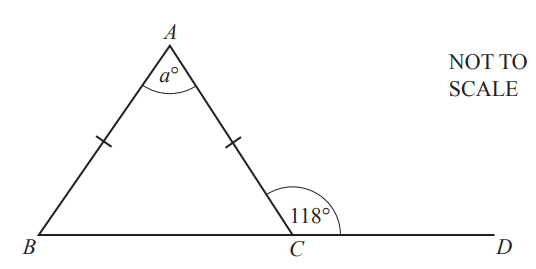
ABC is an isosceles triangle.
BCD is a straight line.
Find the value of a.
a = [2]
(b) Find the size of one interior angle of a regular 10-sided polygon.[3]
(c)
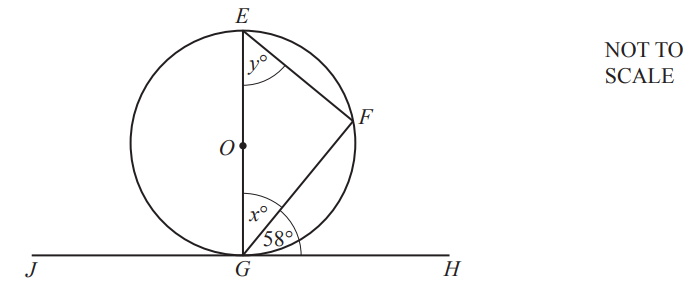
The points E, F and G lie on the circumference of a circle, center O.
JGH is a tangent to the circle.
Find the value of x and the value of y.[2]
x =
y =
(d)
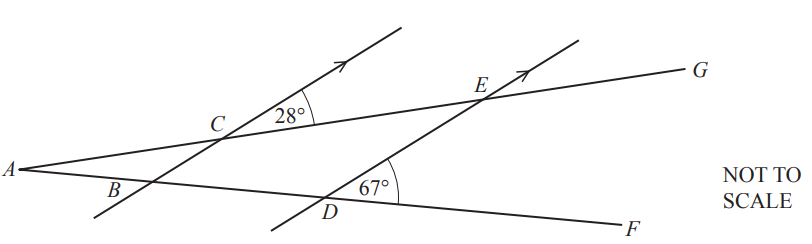
In the diagram AG and AF are straight lines.
Lines BC and DE are parallel.
Find angle CED and give a reason for your answer.
Angle CED = ___ because ___ [2]
(e)
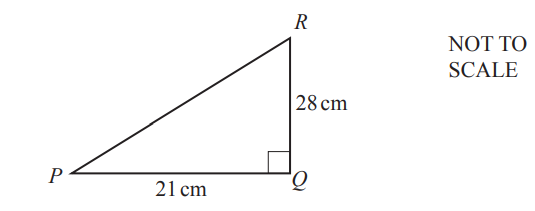
Calculate PR.
PR = cm [2]
Answer/Explanation
Ans:
4(a) 56
4(b) 144
4(c) 32
58
4(d) 28 alternate
4(e) 35
Question
(a) Using a straight edge and compasses only, construct the equilateral triangle ABC. The base AB has been drawn for you.[2]
![]()
(b)
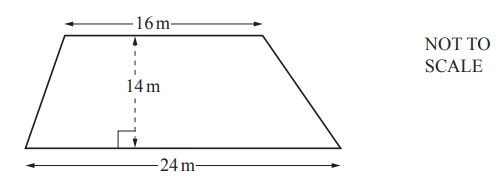
Calculate the area of this trapezium.
m2 [2]
(c) Each interior angle of a regular polygon is 162°.
Calculate the number of sides of the polygon. [3]
(d)
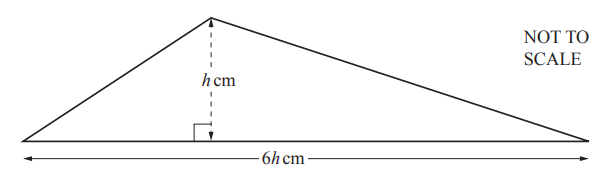
The area of this triangle is 363cm2.
Calculate the value of h.
h = [3]
(e)
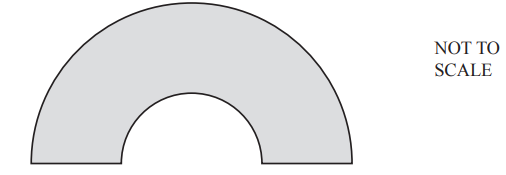
This shape is drawn using two semicircles that have the same center.
The large semicircle has radius 7cm.
The small semicircle has radius 3cm.
Calculate the area of the shape.
cm2 [3]
Answer/Explanation
Ans:
10(a) correct triangle drawn with arcs
10(b) 280
10(c) 20
10(d) 11
10(e) 62.8 or 62.83 to 62.84
Question
Tarak has two fields.
He grows wheat, barley and corn in his fields.
(a) 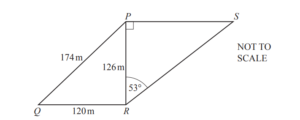
The diagram shows Tarak’s two triangular fields, PQR and PRS.
Angle RPS = 90° and angle PRS = 53°.
PQ = 174m, QR = 120m and PR = 126m.
(i) Show that angle PRQ = 90°.
Answer/Explanation
Ans: Complete method shown and evaluated
(ii) Calculate the area of the quadrilateral PQRS.
Give your answer correct to 4 significant figures.
Answer/Explanation
Ans: 18090 cao
(b) (i) The mass, m tonnes, of wheat grown in 2021 is 4.3 tonnes, correct to 1 decimal place.
Complete this statement about the value of m.
Answer/Explanation
Ans: 4.25 4.35
(ii) In 2020, 2.6 tonnes of barley is grown.
In 2021, 3.25 tonnes of barley is grown.
Show that the percentage increase in barley grown from 2020 to 2021 is 25%.
Answer/Explanation
Ans: Complete method seen
(iii) In 2019, 2.4 tonnes of corn is grown.
In 2020, 20% more corn is grown than in 2019.
In 2021, 20% less corn is grown than in 2020.
Calculate the amount of corn grown in 2021.
Answer/Explanation
Ans: 2.304
Question
(a)
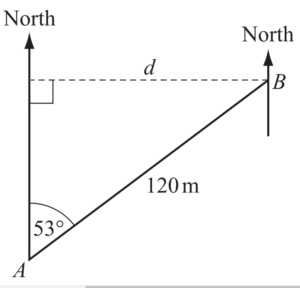
B is 120m from A on a bearing of 053°.
Calculate
(i) the distance d,
(ii) the bearing of A from B
(b)
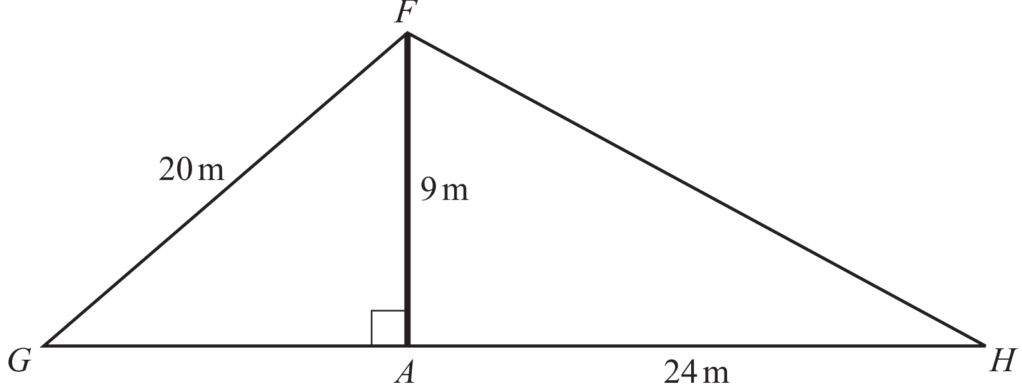
A vertical flagpole, AF, is 9m high.
It is held in place by two straight wires FG and FH.
FG = 20m and AH = 24m.
G, A and H lie in a straight line on horizontal ground.
Calculate
(i) angle FHA,
(ii) the distance GA.
Answer/Explanation
(a)(i) 90+53+\(\angle ABC\) =180
\(\angle ABC\)=180-143
\(\angle ABC\)=37
Now, d=120 Cos 37\((37)^/circ\)
=120\(\times0.7986\)
=95.84
(ii) Bearing means angle measured clockwise from north.
= 233
(b)(i) \(\angle FHA\):
FH=\(\sqrt{(24)^2+(9)^2}\)
=\(\sqrt{576+81}\)
=\(\sqrt{657}\)
= 25.63
\(tan \theta=\frac{9}{24}\)
\(\theta\) = \((\tan)^{-1}(\frac{9}{24})\)
= 20.55
(ii) Distance GA:-
\((20)^2\)=\((GA)^2+9^2\)
GA=\(\sqrt{400-81}\)
= \(\sqrt{319}\)
= 17.9
Question
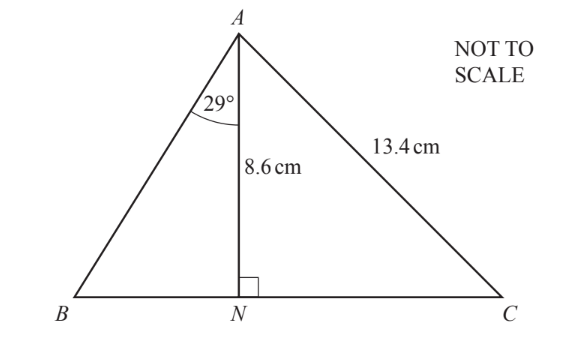
In triangle ABC, AN = 8.6 cm and is perpendicular to BC. Angle BAN = 29° and AC = 13.4 cm.(a) Use trigonometry to calculate
(i) the length of BN,
(ii) angle CAN.
(b) Calculate the length of NC.
▶️Answer/Explanation
(a) (i) $\operatorname{art} 4.77$
(ii) $\operatorname{art} 50.1^{\circ}$
(b) 10.2 to 10.3
Question
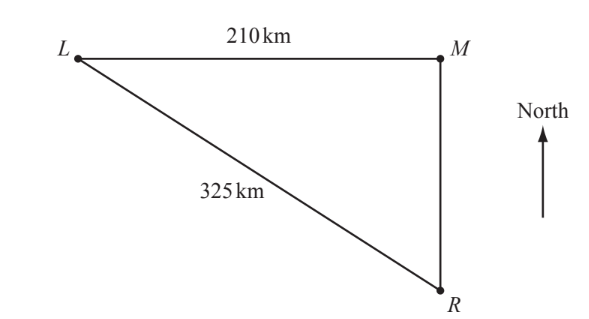
The diagram shows three islands, L, M and R.
L is due west of M and R is due south of M.
LM = 210 km and LR = 325 km.
(a) Calculate the distance RM.
(b) (i) Use trigonometry to calculate angle LRM.
(ii) Find the bearing of L from R.
(c) (i) A ferry travels directly from M to L. It leaves M at 06 15 and arrives at L at 13 45. Calculate the average speed of the ferry in kilometres per hour.
(ii) The ferry then travels the 325 km from L to R at an average speed of 37 km/h. Calculate the time taken. Give your answer in hours and minutes, to the nearest minute.
(iii) The ferry leaves L at 14 00. Use your answer to part (c)(ii) to find the time it arrives at R.
▶️Answer/Explanation
(a) $248 \mathrm{art}$
(b) (i) $40.3^{\circ} \mathrm{art}$
(ii) $319.7(5)^{\circ}$ or $320^{\circ}$
(c) (i) 28
(ii) $8 \mathrm{~h} 47 \mathrm{~min}$
(iii) 2247 or $1047 \mathrm{pm}$
Question
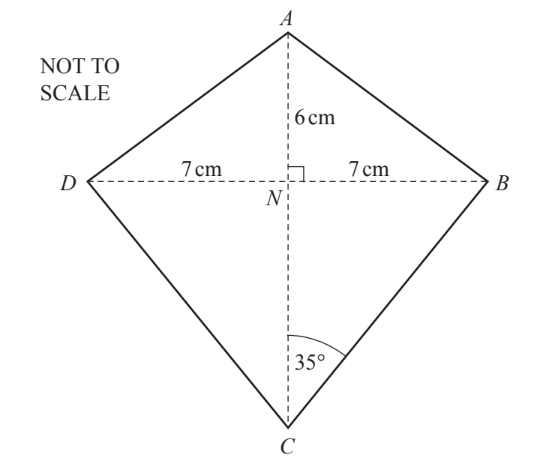
The diagram shows a kite ABCD, with AB = AD and DC = BC.
The diagonals AC and BD intersect at right angles at N.
AN = 6 cm and NB = ND = 7 cm.
Angle BCN = 35°.
(a) (i) What is the mathematical name for triangle BCD?
(ii) Complete the following statement.
(iii) Write down the size of angle DCB.
(b) (i) Use trigonometry to calculate the size of angle NAB.
(ii) Calculate the length of AB.
(c) Use trigonometry to calculate the length of BC.
(d) Calculate the perimeter of the kite.
▶️Answer/Explanation
(a) (i) Isosceles
(ii) $D N C$
(iii) $70^{\circ}$
(b) (i) $49.4^{\circ}$ or $49^{\circ} 24^{\prime}$ art
(ii) 9.22 art
(c) $12.2 \mathrm{art}$
(d) $42.8(4 \ldots)$ or 42.85