Question
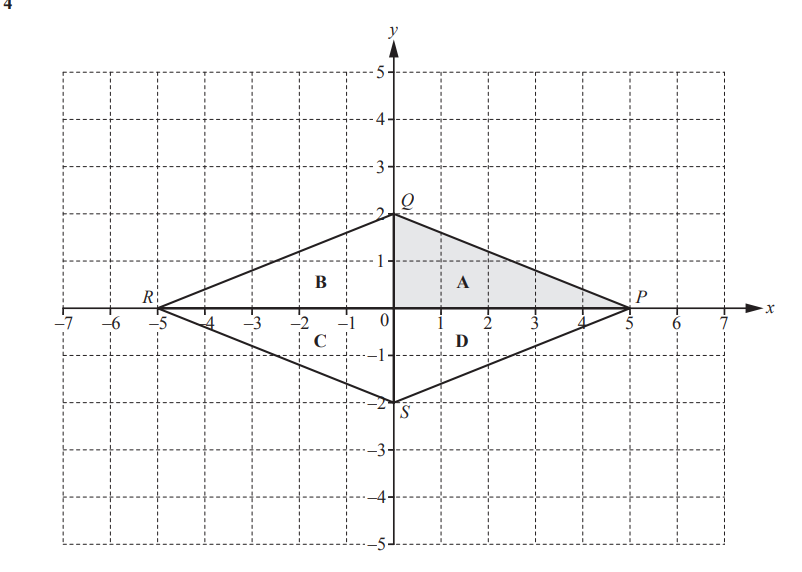
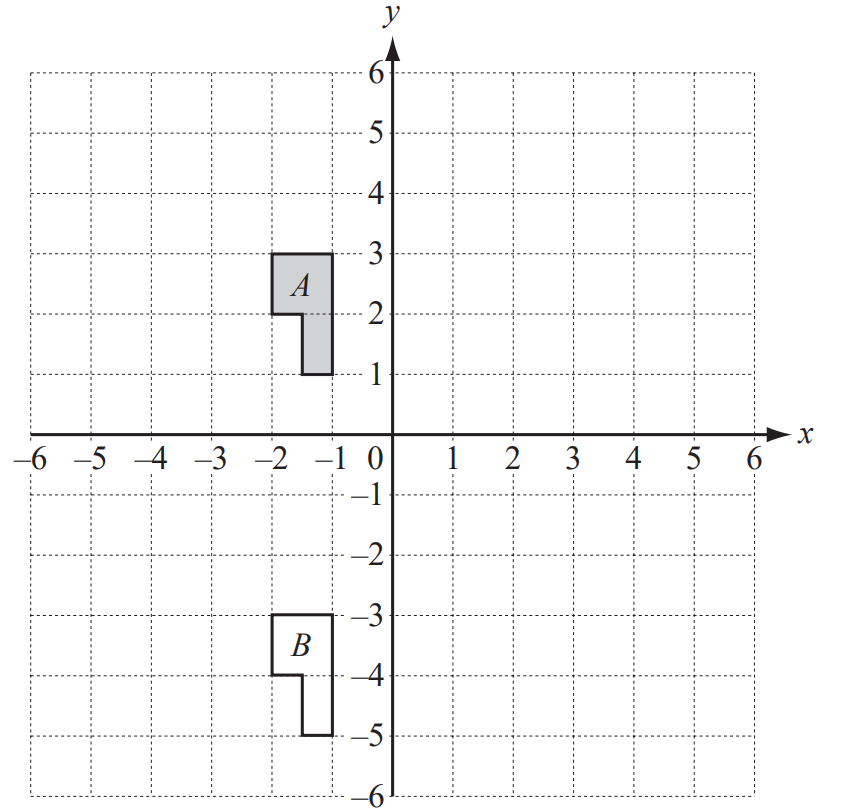
(a) (i) Describe fully the single transformation which maps shape B onto shape A.
(ii) Describe fully the single transformation which maps shape B onto shape C.
(b) (i) Refl ect shape B in the y-axis. Label the image D.
(ii) Rotate shape B through 90° anticlockwise about the origin. Label the image E.
Answer/Explanation
Answer:
(a) (i) Translation
\(\begin{bmatrix}
-7\\-8
\end{bmatrix}\)
(ii) Enlargement
[Scale factor] 0.5
[Centre] (0, 0)
(b) (i) D at ( –2, 4) (–4 , 4) (–3 , 6)
(ii) E at ( –4, 2) ( –4 , 4) ( –6 ,3)
Question
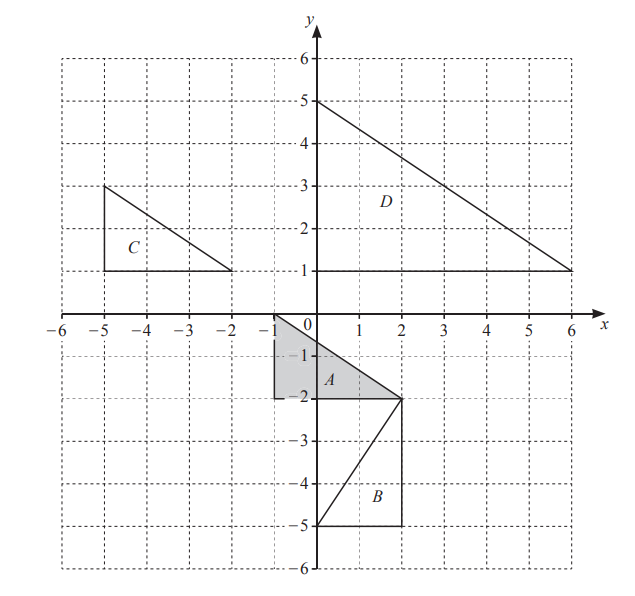
(a)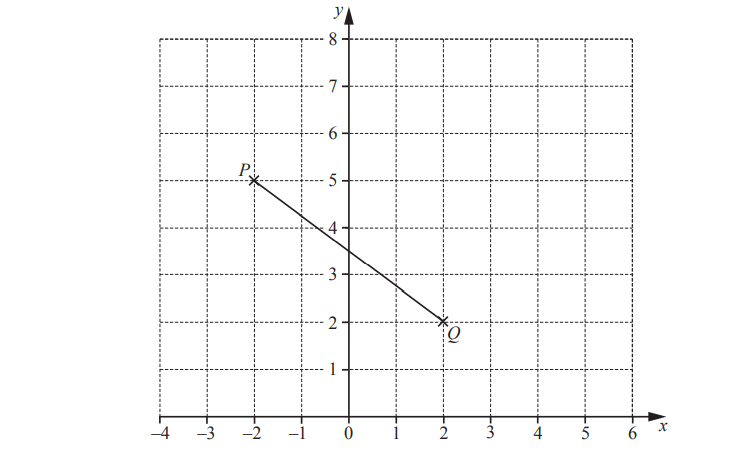
(i) Write down the co-ordinates of point P.
(………………… , …………………)
(ii) Write down the column vector \(\vec{PQ}.\)
(iii)\(\vec{QR}=\begin{pmatrix}3\\ 2\end{pmatrix}\)
On the grid, plot point R
(iv) PQRS is a parallelogram.
On the grid, complete the parallelogram PQRS.
Write down the co-ordinates of point S.
(………………… , …………………)
(b)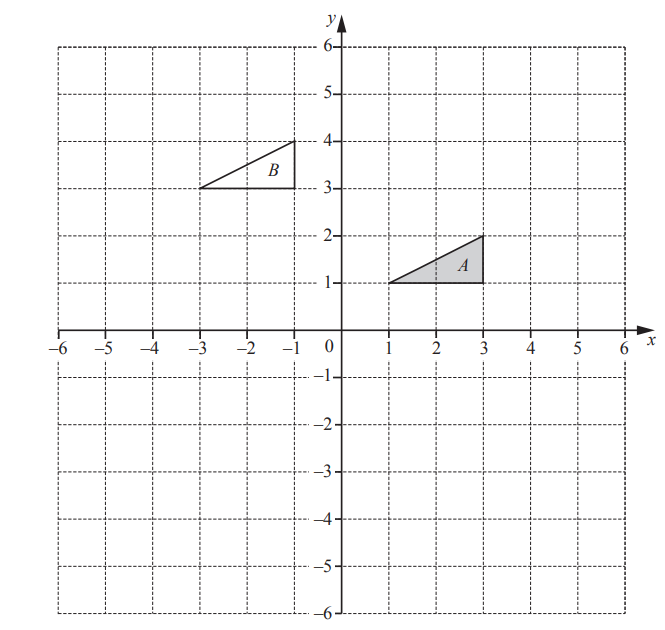
(i) Describe fully the single transformation that maps triangle A onto triangle B.
……………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………..
(ii) On the grid, draw the image of triangle A after a reflection in the line y =-1.
(iii) On the grid, draw the image of triangle A after a rotation through 180° about (0, 0).
Answer/Explanation
(a)(i) (–2, 5)
(ii)\(\begin{pmatrix}4\\ -3\end{pmatrix}\)
(iii) (5, 4) plotted
(iv) Parallelogram PQRS correctly drawn
(1, 7)
(b)(i) Translation
\(\begin{pmatrix}-4\\ 2\end{pmatrix}\)
(ii) Correct reflection
vertices (3, –3), (1, –3), (3, –4)
(iii) Correct rotation
vertices (–3, –1), (–1, –1), (–3, –2)
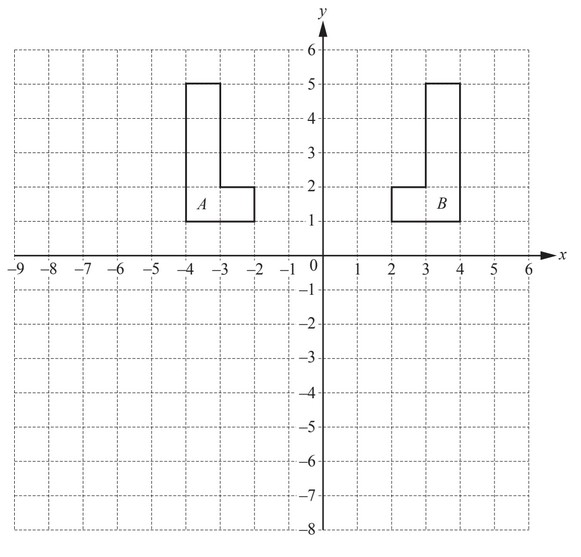
Question

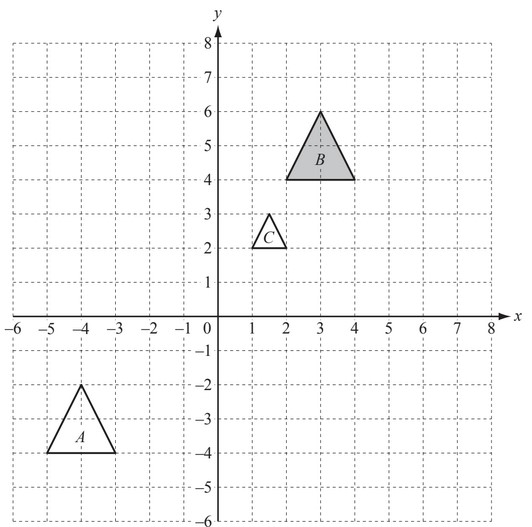
(a) (i) Describe fully the single transformation which maps shape B onto shape A.
(ii) Describe fully the single transformation which maps shape B onto shape C.
(b) (i) Refl ect shape B in the y-axis. Label the image D.
(ii) Rotate shape B through 90° anticlockwise about the origin. Label the image E.
Answer/Explanation
Answer:
(a) (i) Translation
\(\begin{bmatrix}
-7\\-8
\end{bmatrix}\)
(ii) Enlargement
[Scale factor] 0.5
[Centre] (0, 0)
(b) (i) D at ( –2, 4) (–4 , 4) (–3 , 6)
(ii) E at ( –4, 2) ( –4 , 4) ( –6 ,3)
Question
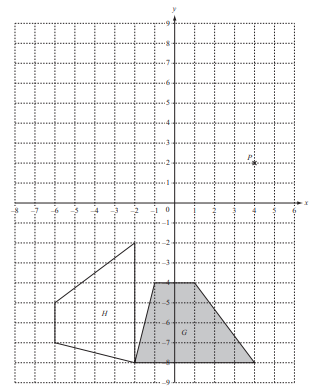
Two congruent quadrilaterals, G and H, and a point P are shown on this 1cm2 grid.
(a) (i) Write down the mathematical name of the shaded quadrilateral.
Answer/Explanation
Ans: Trapezium
(ii) Calculate the area of the shaded quadrilateral.
Give the units of your answer.
Answer/Explanation
Ans: 16 cm2
(b) Describe fully the single transformation that maps quadrilateral G onto quadrilateral H.
Answer/Explanation
Ans: Rotation
90°[anti-clockwise] oe
[centre] (–2, –8)
(c) On the grid, draw the images of quadrilateral G after the following transformations.
(i) Refl ection in the line y = 0.
Answer/Explanation
Ans: Correct reflection in y = 0
(ii) Translation by the vector \(\binom{-5}{7}.\)
Answer/Explanation
Ans: Translation 5 left and 7 up
(iii) Enlargement by scale factor 0.5 with centre P.
Answer/Explanation
Ans: Correct Enlargement
(d) On quadrilateral H mark, with an arc, an obtuse angle.
Answer/Explanation
Ans: Obtuse angle marked
Question
(a) On each of the following shapes draw any lines of symmetry.
(i) 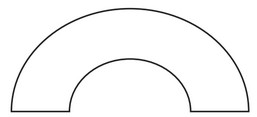
(ii) 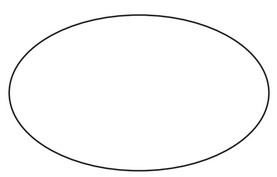
(b) Complete this shape by shading one square so that it has rotational symmetry of order 2.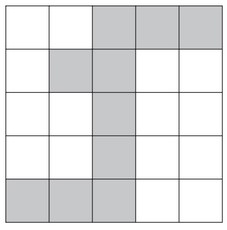
(c) 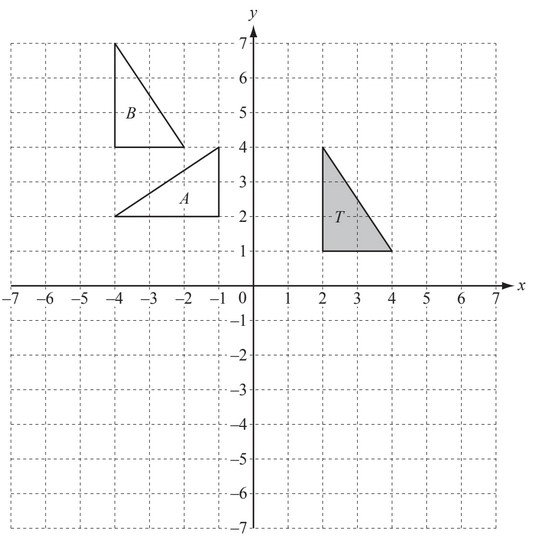
On the grid, draw the image of triangle T after a
(i) refl ection in the line x = 4,
(ii) translation by the vector \(\binom{-5}{-4}\)
(iii) rotation, centre (4, 1) through 180°.
(d) Describe fully the single transformation that maps
(i) triangle T onto triangle A,
(ii) triangle T onto triangle B.
Answer/Explanation
Answer:
(a) (i) one correct line
(ii) only two correct lines
(b) correct square
(c) (i) correct reflection
(ii) correct translation
(iii) correct rotation
(d) (i) rotation
centre (0,0)
angle 90°
[anticlockwise]
(ii) translation
\(\binom{-6}{3}\)
Question
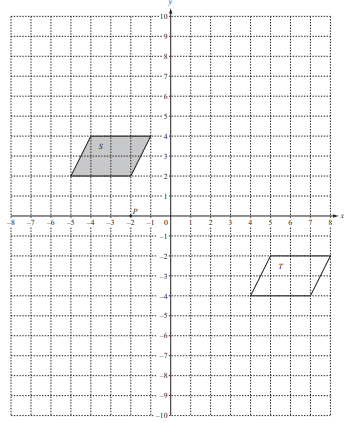
The diagram shows two shapes, S and T, on a 1cm2 grid.
P is the point (–2, 0).
(a) (i) Write down the mathematical name of shape S.
Answer/Explanation
Ans: Parallelogram
(ii) How many lines of symmetry does shape S have?
Answer/Explanation
Ans: 0
(b) Describe the single transformation that maps shape S onto shape T.
Answer/Explanation
Ans: Translation
\(\binom{9}{-6}\)
(c) On the grid,
(i) draw the refl ection of shape S in the y-axis,
Answer/Explanation
Ans: (1, 4), (4, 4), (5, 2), (2, 2).
(ii) draw the rotation of shape S about (0, 0) through 90° anti-clockwise.
Answer/Explanation
Ans: (−4, −1), (−4, −4), (−2, −5), (−2, −2)
(d) On the grid, draw the enlargement of shape S with scale factor 2 and centre P (–2, 0).
Label the image E.
Answer/Explanation
Ans: (–6,8), (0,8), (–8,4), (–2,4)
(e) (i) Work out the area of shape S.
Answer/Explanation
Ans: 6
(ii) How many shapes, identical to shape S, will fi ll shape E completely?
Answer/Explanation
Ans: 4
(iii) Work out the area of shape E.
Answer/Explanation
Ans: 24
Question
(a) 
(i) Write down the order of rotational symmetry of this shape.
Answer/Explanation
Ans: 2
(ii) Draw the lines of symmetry on the shape.
Answer/Explanation
Ans: Two correct lines of symmetry drawn
(b)
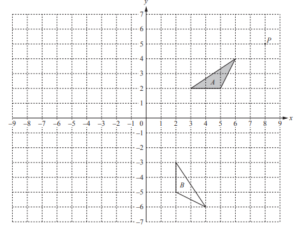
(i) On the grid, reflect triangle A in the line x = –1.
Answer/Explanation
Ans: Correct reflection
(ii) On the grid, enlarge triangle A with centre P and scale factor 3.
Answer/Explanation
Ans: Correct enlargement
(iii) Describe fully the single transformation that maps triangle A onto triangle B.
Answer/Explanation
Ans: Rotation
90° clockwise oe
[Centre] (0, 0) oe
Question
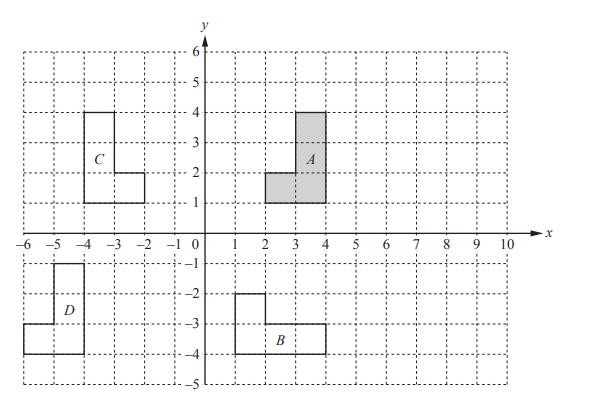
The diagram shows four shapes A, B, C and D.
(a) Describe fully the single transformation that maps shape A onto
(i) shape B,
Answer/Explanation
Ans: rotation
[centre] (0, 0) oe
90° clockwise oe
(ii) shape C,
Answer/Explanation
Ans: reflection
y-axis or x = 0
(iii) shape D.
Answer/Explanation
Ans: translation
\(\binom{-8}{-5}\)
(b) On the grid, draw the enlargement of shape A by scale factor 2 and centre (–1 , 2).
Answer/Explanation
Ans: correct enlargement shown
Question
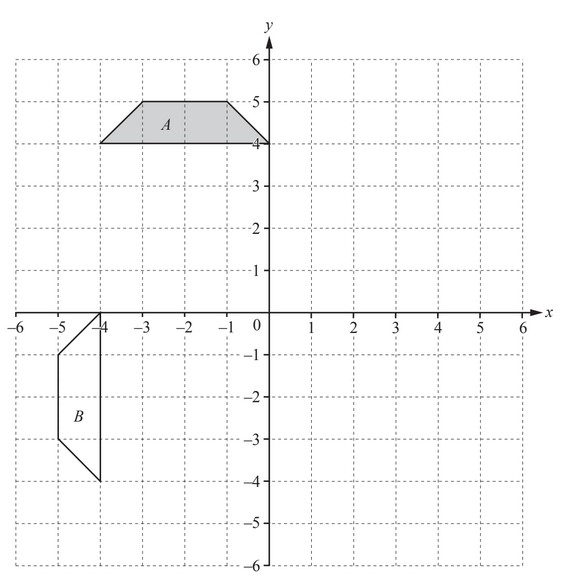
The diagram shows two trapeziums, A and B, on a 1\(cm^2\) grid.
(a) Find the area of trapezium A.
Give the units of your answer.
(b) (i) Describe fully the single transformation that maps trapezium A onto trapezium B.
(ii) On the grid, translate trapezium A by the vector \(\binom{5}{-2}\)
(iii) On the grid, enlarge trapezium A with centre (0, 0) and scale factor 0.5
Answer/Explanation
Answer:
(a) 3
\(cm^2\)
(b) (i) Rotation
90° [anticlockwise] oe
[Centre] (0,0) oe
(ii) Correct trapezium
(iii) Correct trapezium
Question
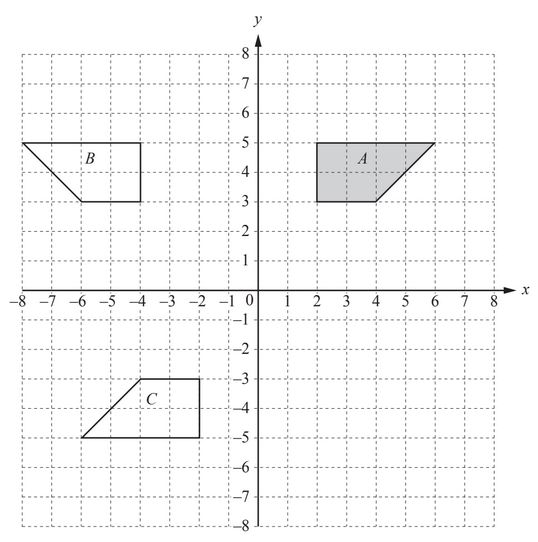
(a) On the grid, draw the image of shape A after a translation by the vector \(\begin{pmatrix}
-2\\-6
\end{pmatrix}\)
(b) (i) On the grid, draw the image of shape A after an enlargement, scale factor 2, centre (4, 4).
(ii) Write down the scale factor of the enlargement that maps the image in part (b)(i)
back onto shape A.
(c) Describe fully the single transformation that maps shape A onto shape B.
(d) Describe fully the single transformation that maps shape A onto shape C.
Answer/Explanation
Answer:
(a) Correct image, points at
(0,–3), (0,–1), (2,–3) and (4,–1)
(b) (i) Correct image, points at
(0, 6), (8, 6), (4, 2) and (0, 2)
(ii) \(\frac{1}{2}\)
(c) Reflection
[in mirror line] x = –1 oe
(d) Rotation
[centre] (0, 0) oe
[angle] 180° oe
Question
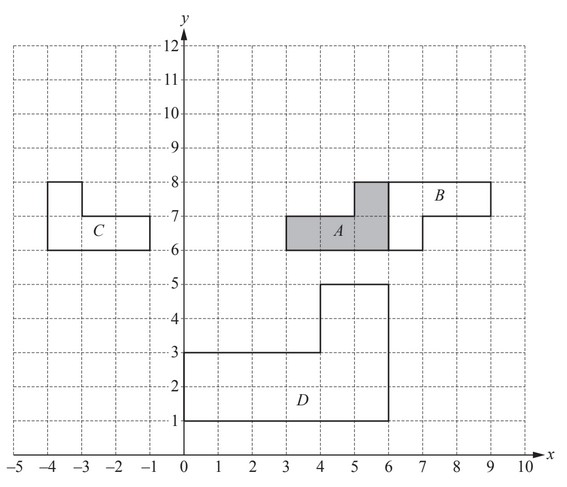
The diagram shows four shapes A, B, C and D.
(a) Describe fully the single transformation that maps shape A onto
(i) shape B,
(ii) shape C,
(iii) shape D.
(b) On the grid, draw the image of shape A after a translation by the vector \(\begin{pmatrix}
-3\\2
\end{pmatrix}\)
Answer/Explanation
Ans:
(a) (i) rotation
[centre] (6, 7)
180° oe
(ii) reflection
x =1
(iii) enlargement
[centre] (6, 11)
scale factor 2
(b) correct translation shown
Question
(a) The diagram shows a triangle, A, on a 1 \(cm^2\) grid.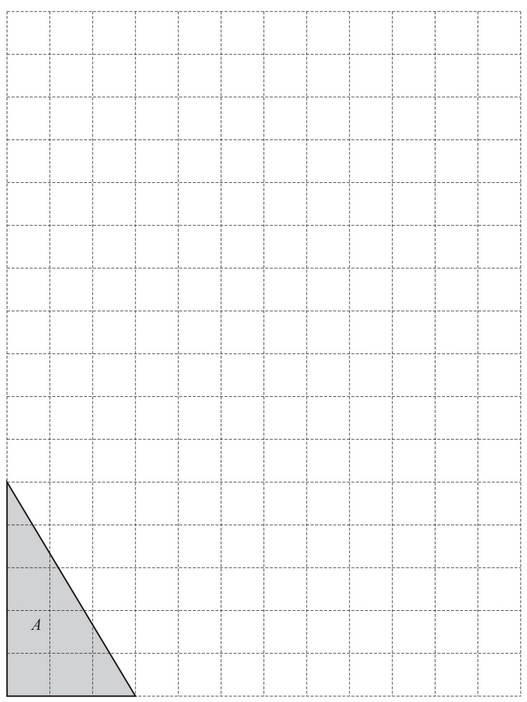
(i) Find the area of triangle A.
…………………………. \(cm^2\)
(ii) On the grid, draw an enlargement of triangle A with scale factor 2.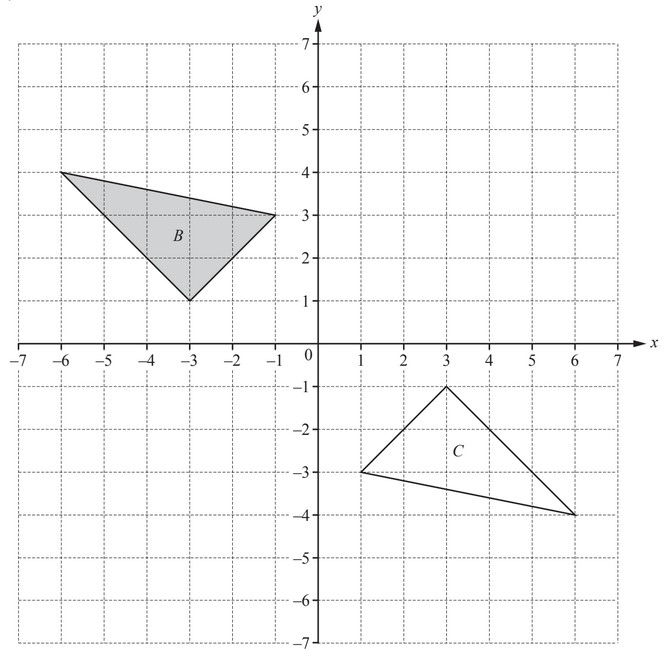
(i) Describe fully the single transformation that maps triangle B onto triangle C.
(ii) Reflect triangle B in the line y = –1.
(iii) Translate triangle B by the vector \(\begin{pmatrix}
5\\1
\end{pmatrix}\)
Answer/Explanation
Ans:
(a)(i) 7.5
(ii) Correct enlargement
(b) (i) Rotation
[centre] (0,0) oe
180°
(ii) Correct reflection with points
(–3,–3), (–1,–5) and (–6,–6)
(iii) Correct translation with points
(4,4), (2,2) and (–1,5)
Question
(a) 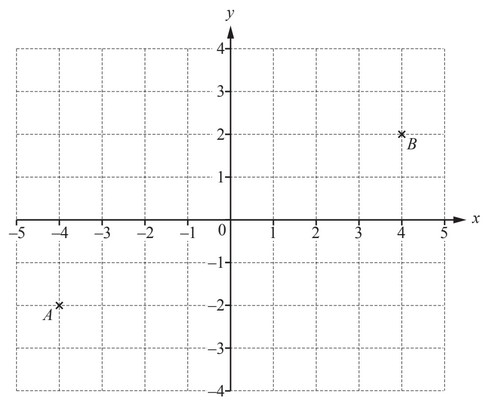
(i) Plot point C at (–4, 2).
(ii) Write down the mathematical name of the triangle formed by joining the points A, B and C.
(iii) Write down the vector \(\overheadarrow{AB}\)
\(\overheadarrow{AB} = ( )\)
(iv) (a) Find the gradient of the line AB.
(b) Write down the equation of the line AB.
y = …………………………………………
(b) (i) Complete the table of values for \(y = x^2 + x -5\).
(ii) On the grid below, draw the graph of \(y = x^2 + x – 5\) for \(-4 \leq x \leq 4\).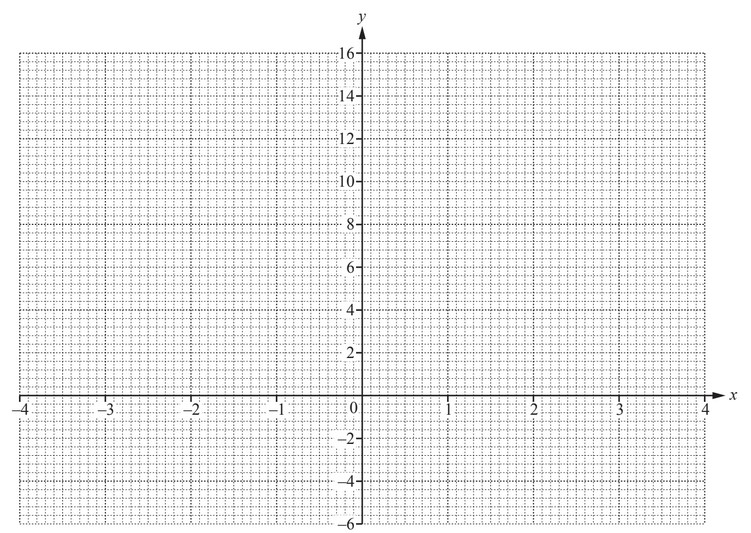
(iii) Use your graph to solve the equation \(x^2 + x – 5 = 0\)
x = ……………….. or x = ………………..
Answer/Explanation
Ans:
(a) (i) Correct point plotted
(ii) Right-angled or scalene
(iii) 8
4
(iv) (a) 0.5 oe
(iv) (b) [y =] 0.5x oe
(b) …1 …–5 –5…1 15
(ii) Correct curve
(iii) –2.8 1.8
Question
(a) Write down the mathematical name of the shaded polygon.
(b) Describe fully the single transformation that maps the shaded polygon onto polygon A.
(c) Describe fully the single transformation that maps the shaded polygon onto polygon B.
(d) On the grid, draw the reflection of the shaded polygon in the line x = 2.
(e) On the grid, draw the rotation of the shaded polygon through 90° anti-clockwise about the origin.
Answer/Explanation
Answer:
(a) Quadrilateral
(b) Enlargement
[Scale factor] 3
[Centre] (–3, –1)
(c) Translation
\(\begin{pmatrix}
10\\-7
\end{pmatrix}\)
(d) Vertices (6, 2), (7, −1),
(8, −1), (9, 1)
(e) Vertices (−2, −2), (1, −3),
(1, −4), (−1, −5)
Question
The diagram shows two shapes A and B.
(a) Describe fully the single transformation that maps shape A onto shape B.
(b) (i) Reflect shape B in the line y = 0 and label this shape C.
(ii) Describe fully the single transformation that maps shape A onto shape C.
(c) (i) Enlarge shape A by scale factor 3, centre (–2, 5). Label this shape D.
(ii) How many times bigger is the area of shape D than the area of shape A?
Answer/Explanation
Answer:
(a) reflection
y-axis oe
(b) (i) correct reflection at
(2, -1), (4, -1), (4, -5), (3, -5), (3, -2), (2, -2)
(ii) rotation
[centre] (0, 0) oe
\(180^o\)
(c) (i) correct enlargement at
(-8, 5). (-5, 5), (-5, -4), (-2, -4), (-2, -7), (-8, -7)
(ii) 9
Question
(a)
(i) Write down the co-ordinates of point P.
(………………… , …………………)
(ii) Write down the column vector \(\vec{PQ}.\)
(iii)\(\vec{QR}=\begin{pmatrix}3\\ 2\end{pmatrix}\)
On the grid, plot point R
(iv) PQRS is a parallelogram.
On the grid, complete the parallelogram PQRS.
Write down the co-ordinates of point S.
(………………… , …………………)
(b)
(i) Describe fully the single transformation that maps triangle A onto triangle B.
……………………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………………..
(ii) On the grid, draw the image of triangle A after a reflection in the line y =-1.
(iii) On the grid, draw the image of triangle A after a rotation through 180° about (0, 0).
Answer/Explanation
(a)(i) (–2, 5)
(ii)\(\begin{pmatrix}4\\ -3\end{pmatrix}\)
(iii) (5, 4) plotted
(iv) Parallelogram PQRS correctly drawn
(1, 7)
(b)(i) Translation
\(\begin{pmatrix}-4\\ 2\end{pmatrix}\)
(ii) Correct reflection
vertices (3, –3), (1, –3), (3, –4)
(iii) Correct rotation
vertices (–3, –1), (–1, –1), (–3, –2)
Question
The diagram shows a quadrilateral PQRS which is made from four congruent triangles A, B, C and D.
(a) Write down the mathematical name for the quadrilateral PQRS.
…………………………………………
(b) (i) Write down the co-ordinates of S.
(……………. , …………….)
(ii) Measure the obtuse angle PSR.
…………………………………………
(c) (i) Measure the length of the line PQ.
…………………………………… cm
(ii) Work out the perimeter of the quadrilateral PQRS.
…………………………………… cm
(d) Describe fully the single transformation that maps
(i) triangle A onto triangle B,
……………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………
(ii) triangle A onto triangle C.
……………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………
(e) On the grid, draw the image of triangle D after a translation by the vector \(\begin{pmatrix}1\\ -2\end{pmatrix}\)
Answer/Explanation
(a) Rhombus
(b)(i) (0, –2)
(ii) 136
(c)(i) 5.4
(ii) 21.5 or 21.6
(d)(i) Reflection
y-axis oe
(ii) Rotation
180 oe
(0, 0) oe
(e) Triangle (1, –2) (1, –4) (6, –2)
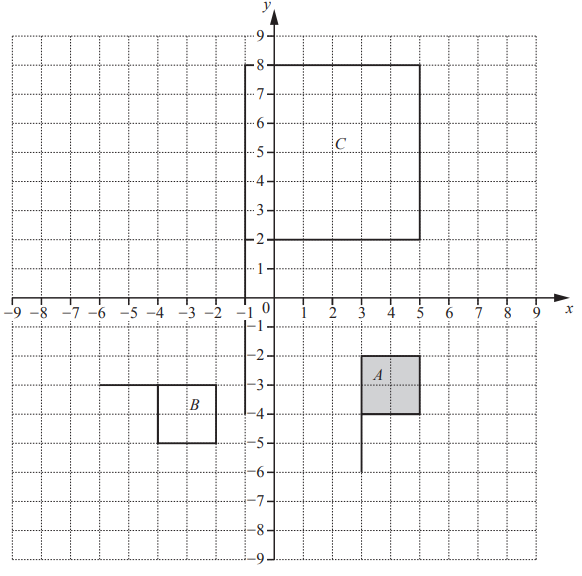
Question
The diagram shows four shapes, A, B, C and D, drawn on a \(1cm^{2}\) grid.
(a) Find the area of shape B.
………………………………….. \(cm^{2}\)
(b) Describe fully the single transformation that maps
(i) shape A onto shape B,
……………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………
(ii) shape B onto shape C,
……………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………
(iii) shape C onto shape D.
……………………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………………
(c) On the grid, draw the image of shape D after a reflection in the line x =-1
Answer/Explanation
(a)4
(b)(i)Rotataion
90 clockwise oe
[centre] (0, –2)
(ii)Translation
\(\binom{-4}{2}\)
(iii)Enlargement
[scale factor] 2
[centre] (–2, –7)
(c)Correct reflection
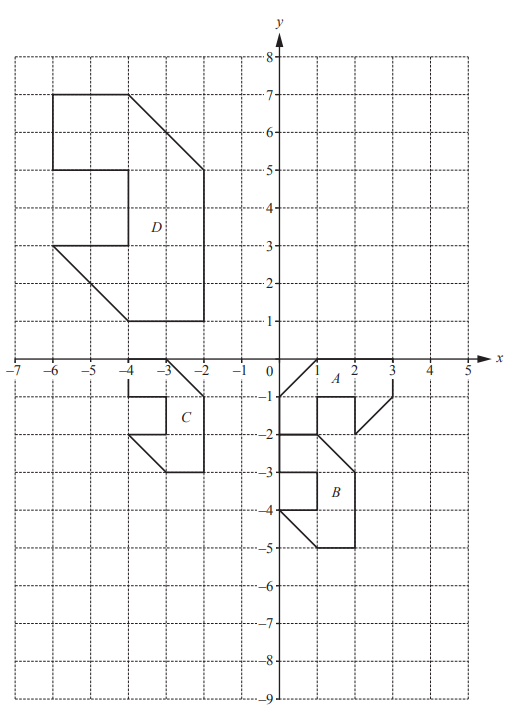
Question
(a) Describe fully the single transformation that maps shape A onto shape B.[3]
(b) Describe fully the single transformation that maps shape A onto shape C.[3]
(c) On the grid, draw the image of shape A after a translation by the vector \(\binom{3}{1}\). [2]
(d) On the grid, draw the image of shape B after a reflection in the line y = 1. [2]
Answer/Explanation
Ans:
7(a) Rotation
[centre] (0, 0) oe
90[°] clockwise oe
7(b) Enlargement
[centre] (5, −7)
[sf=] 3
7(c) Correct shape plotted with points
(6, −1) (8, −1) (6, −3) (8, −3)
(6, −5)
7(d) Correct shape plotted with points
(−2, 5) (−6, 5) (−2, 7) (−4, 5)
(−4, 7)
Question
(a) Describe fully the single transformation that maps
(i) triangle A onto triangle B,
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(ii) triangle A onto triangle C,
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(iii) triangle A onto triangle D.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(b) On the grid, draw the image of triangle A after a reflection in the line x =-2.
Answer/Explanation
(a)(i) Rotation
[centre] (2, −2)
90° [anticlockwise]
(ii) Translation\( \begin{pmatrix}-4\\ 3\end{pmatrix}\)
(iii) Enlargement
[centre] (−2, −5)
[sf] 2
(b) Correct reflection of triangle points at (−3, 0) (−3, −2) (−6, −2)
Question
The grid shows a point E and four quadrilaterals, A, B, C and D.
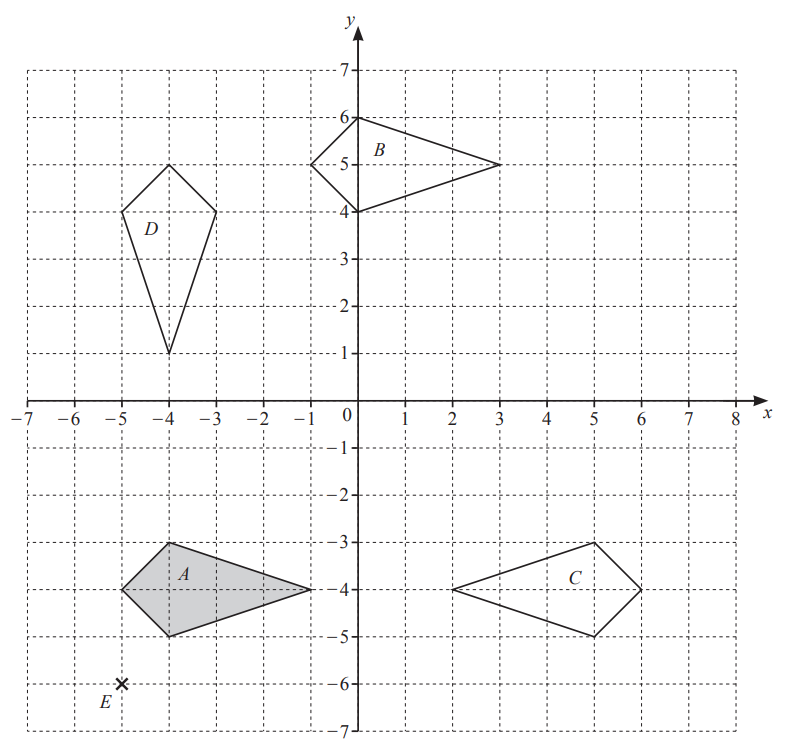
(a) Write down the mathematical name of shape A.
…………………………………………..
(b) Describe fully the single transformation that maps
(i) shape A onto shape B,
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(ii) shape A onto shape C,
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(iii) shape A onto shape D.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(c) (i) Write down the coordinates of the point E.
( ……………… , ……………… )
(ii) On the grid, draw the image of shape A after an enlargement by scale factor 3, centre E.
Answer/Explanation
(a) Kite
(b)(i) Translation
\(\begin{pmatrix}4\\ 9\end{pmatrix}\0
(ii) Reflection
x = 0.5 oe
(iii) Rotation
90° clockwise oe
[centre] (0, 0) oe
(c)(i) (−5, −6)
(c)(ii) Image at (−5, 0), (−2, 3), (7, 0),(−2, −3)
Question
(a)
(i) On the grid, draw the image of
(a) shape A after an enlargement with scale factor \frac{1}{2} , centre (3,-5)
(b) shape B after a reflection in the line y =-3.
(ii) Describe fully the single transformation that maps triangle C onto triangle D.
……………………………………………………………………………………………………………………………
…………………………………………………………………………………………………………………………..
(b)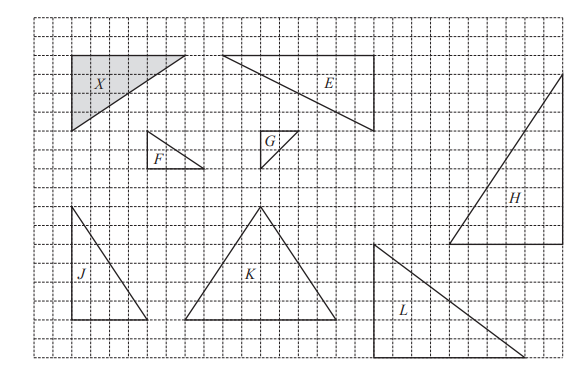
For the triangles shown on the grid, write down the letter of each triangle that is
(i) congruent to triangle X,
………………………………………….
(ii) similar to triangle X.
………………………………………….
Answer/Explanation
(a)(i)(a) Correct enlargement (3, –3), (4.5, –6), (3, –7), (1.5, –6)
(a)(i)(b) Correct reflection (–6, –2), (–6, 0), (–5, –1), (–4, 2)
(a)(ii) Rotation
[Centre] (–4, 4)
90° clockwise
(b)(i) J
(b)(ii) F, H, [J]
Question
(a) The diagram shows three quadrilaterals, A, B and C, on a 1cm2 grid.
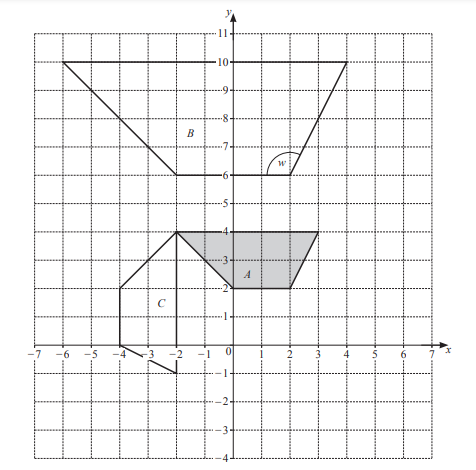
(i) (a) Write down the mathematical name for quadrilateral B.
Answer/Explanation
Ans: Trapezium
(b) Work out the area of quadrilateral B.
Give the units of your answer.
Answer/Explanation
Ans: 28
cm2
(ii) Measure angle w.
Answer/Explanation
Ans: 117
(iii) Describe fully the single transformation that maps
(a) quadrilateral A onto quadrilateral B,
Answer/Explanation
Ans: Enlargement
[centre] ( 2, -2)
[scale factor] 2
(b) quadrilateral A onto quadrilateral C.
Answer/Explanation
Ans: Rotation
[centre] ( − 2, 4)
90° clockwise oe
(b) The diagram shows a parallelogram and a line AB on a 1cm2 grid.
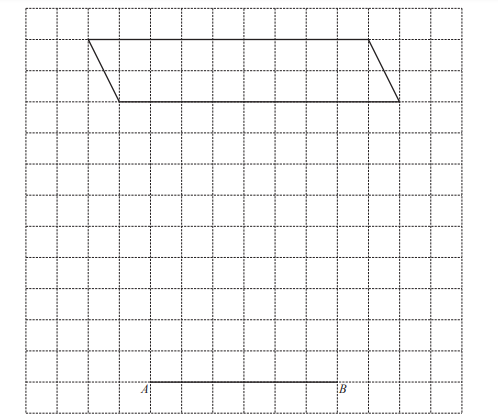
On the grid, complete a triangle, ABC, that has the same area as the parallelogram.
Answer/Explanation
Ans: A correct triangle drawn
Question
The diagram shows three triangles A, B and C on a grid.
Triangle A is shaded.
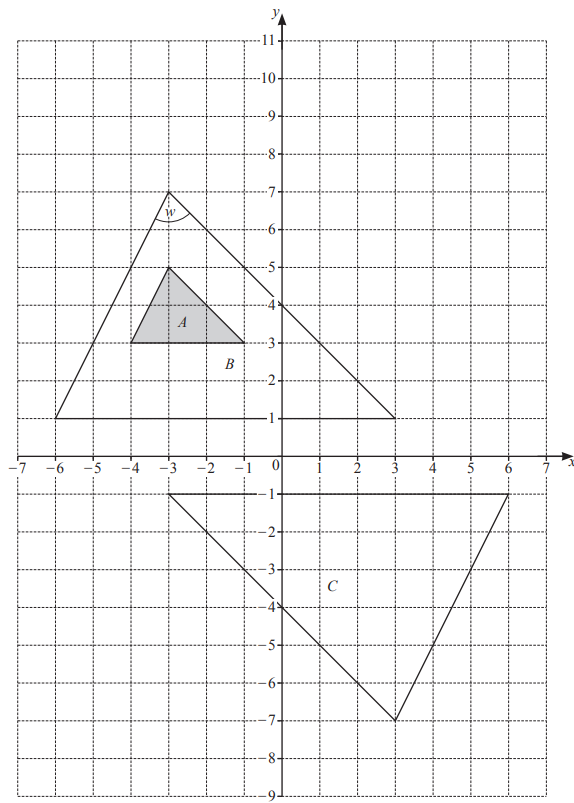
(a) Measure angle w.
Angle w = …………………………………………
(b) Explain why triangle B is congruent to triangle C.
…………………………………………………………………………………………………………………………………..
(c) Describe fully the single transformation that maps
(i) triangle A onto triangle B,
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(ii) triangle B onto triangle C.
……………………………………………………………………………………………………………………………
……………………………………………………………………………………………………………………………
(d) On the grid, draw the image of
(i) shape A after a translation by the vector \(\begin{pmatrix}7\\ -1\end{pmatrix}\)
(ii) shape A after a reflection in the line y =-1.
Answer/Explanation
(a) 72
(b) Correct reason
(c)(i) Enlargement
[centre] ( − 3, 4)
[scale factor] 3
(ii)Rotation
[centre] (0,0) oe
180° oe
(d)(i) Correct translation
(3,2),(4,4),(6,2)
(ii) Correct reflection
( −1,-5), ( −3,- 7 ), (−4,–5)
Question
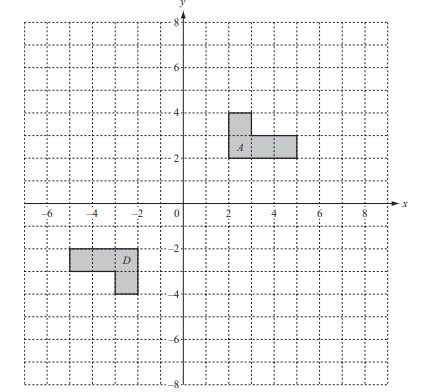
Two shapes A and D are shown on the grid.
(a) (i) Reflect shape A in the line x = 0. Label this image B.
Answer/Explanation
Ans: Image at (–5,2), (–2,2), (–2,4), (–3,4), (–3,3), (–5,3)
(ii) Rotate shape A through 180° about (2, 4). Label this image C.
Answer/Explanation
Ans: Image at (2,4), (2,6), (–1,6), (–1,5), (1,5), (1,4)
(iii) Enlarge shape A with scale factor 2 and centre (3, 7). Label this image E.
Answer/Explanation
Ans: Image at (1,1), (3,1), (3, –1), (7, –1), (7, –3), (1, –3)
(b) Describe fully the single transformation that maps shape D onto
(i) shape B,
Answer/Explanation
Ans: Reflection, y = 0 or x axis
(ii) shape C.
Answer/Explanation
Ans: Translation, \(\binom{4}{8}\)
Question
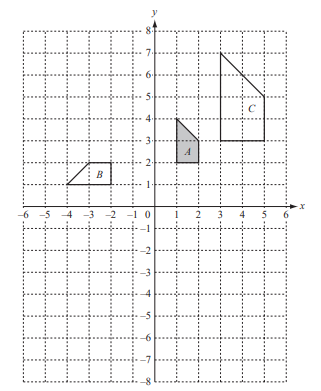
Shapes A, B and C are shown on the grid.
(a) Describe fully the single transformation which maps
(i) shape A onto shape B,
Answer/Explanation
Ans: Rotation,
90° anticlockwise oe,
(centre) (0, 0), origin, O
(ii) shape A onto shape C.
Answer/Explanation
Ans: Enlargement,
(scale factor) 2,
(centre) (–1, 1)
(b) On the grid, draw the image of shape A after
(i) translation by the vector \(\binom{3}{-4},\)
Answer/Explanation
Ans: correct translation
(ii) reflection in the line y = –1.
Answer/Explanation
Ans: correct reflection
Question
(a)
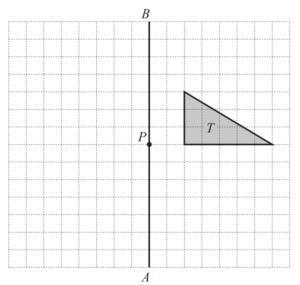
(i) Reflect triangle T in the line AB.
Label your image X.
(ii) Rotate triangle T through 90° clockwise about the point P.
Label your image Y.
(b)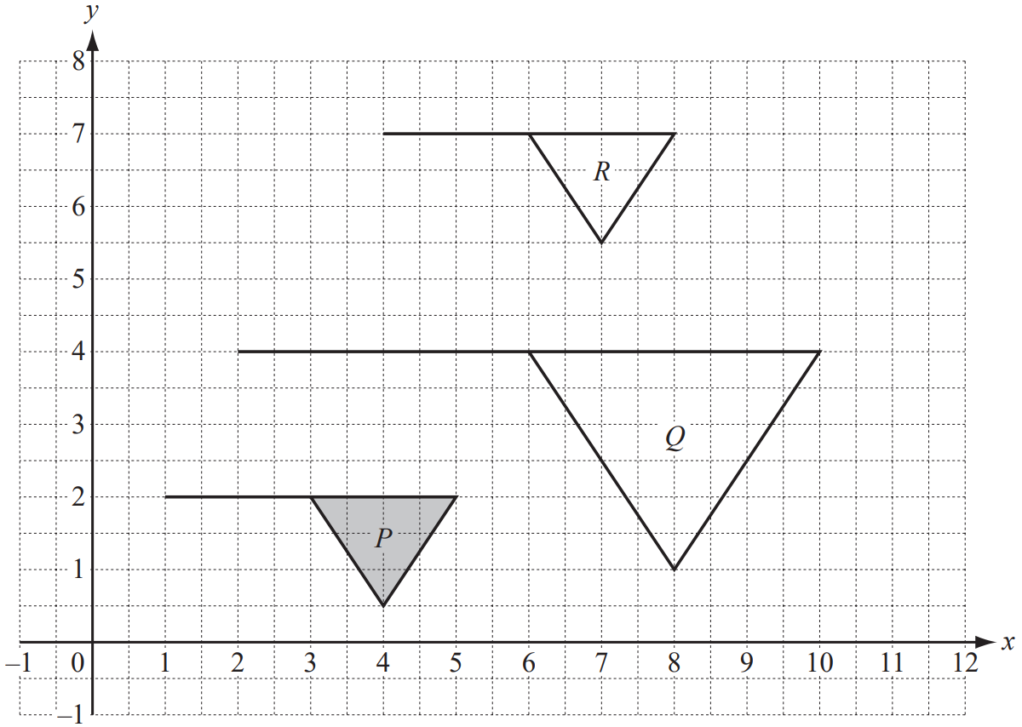
Describe the single transformation which maps
(i) flag P onto flag Q,
(ii) flag P onto flag R.
Answer/Explanation
(a)(i)
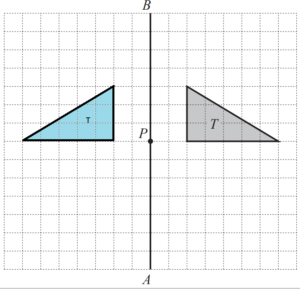
Image X is shown above
Question
The diagram shows two shapes A and B.
(a) Describe fully the single transformation which maps A onto B.
(b) On the grid, draw the line x = 2
(c) On the grid, draw the image of shape A after the following transformations.
(i) Reflection in the line x = 2. Label the image C.
(ii) Enlargement, scale factor 2, centre (0, 0). Label the image D.
Answer/Explanation
(a) Translation
(b)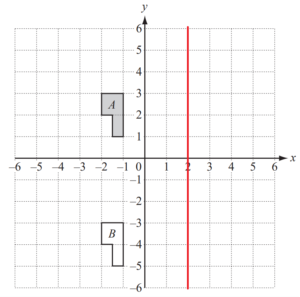
(c)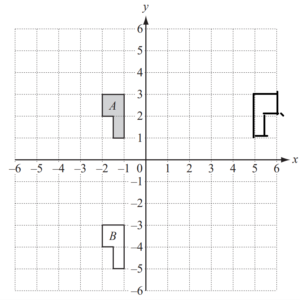
Question
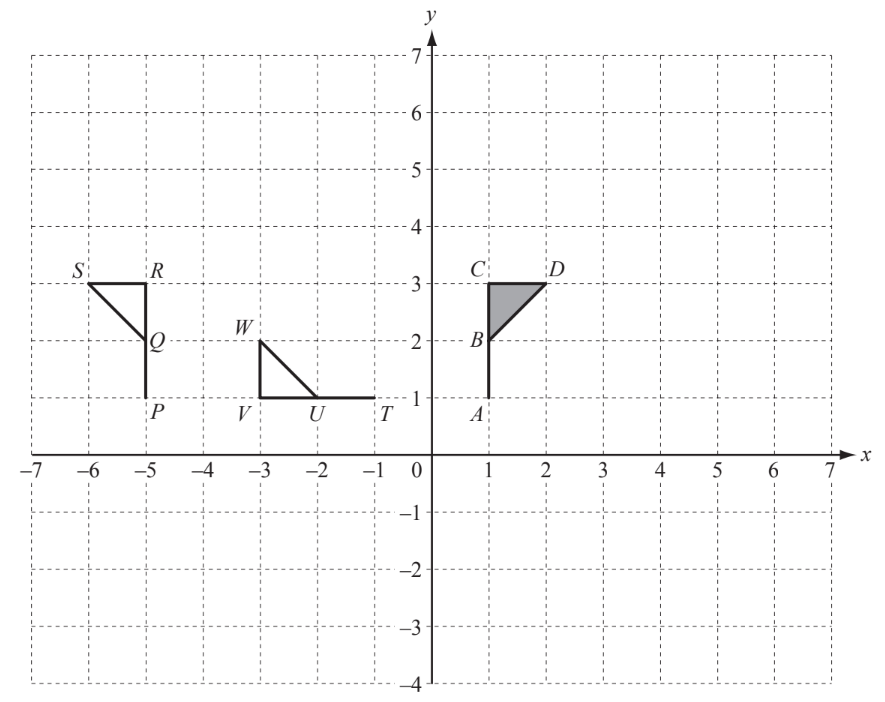
(a) On the grid, draw the image of
(i) the flag $A B C D$ after translation by $\left(\begin{array}{c}4 \\ -3\end{array}\right)$,
(ii) the flag $A B C D$ after enlargement, scale factor 2 , centre the origin,
(iii) the flag $A B C D$ after reflection in the $x$-axis.
(b) Describe fully the single transformation which maps $A B C D$ onto $P Q R S$.
(c) Describe fully the single transformation which maps ABCD onto TUVW.
▶️Answer/Explanation
(a) (i) correct image
(ii) correct image
(iii) correct image
(b) Reflection, $x=-2$
(c) Rotation, origin, $90^{\circ}$ (anti-clockwise or $\left.+90^{\circ}\right)$
Question
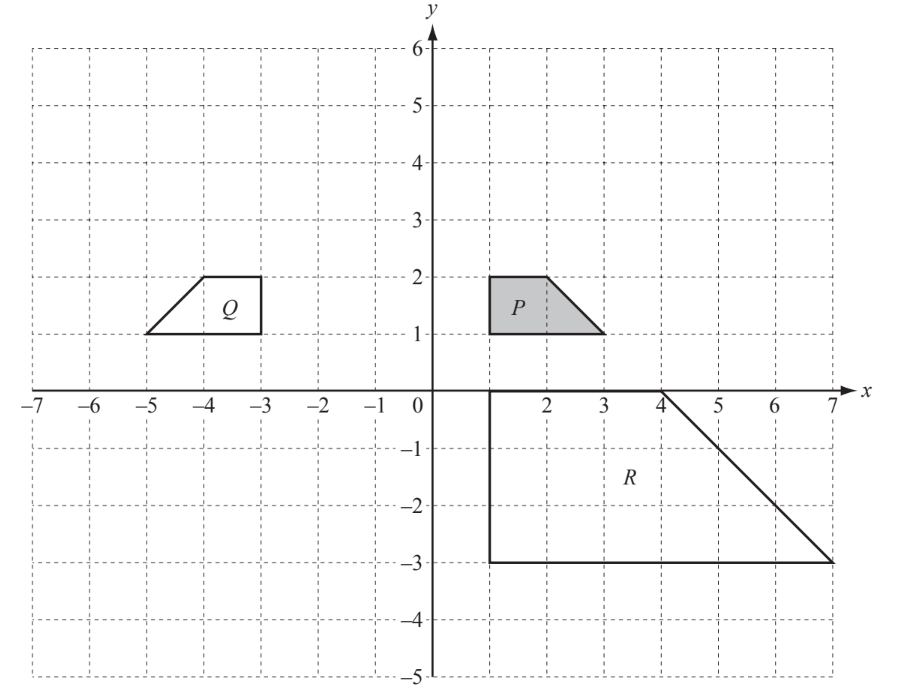
Shapes $P, Q$, and $R$ are shown on the grid.
(a) On the grid, draw the image of shape $\boldsymbol{P}$ after
(i) a rotation through $180^{\circ}$ about the origin,
(ii) a reflection in the line $y=3$,
(iii) a translation by the vector $\left(\begin{array}{r}-5 \\ 3\end{array}\right)$.
(b) Describe fully the single transformation which maps
(i) shape $P$ onto shape $Q$,
(ii) shape $P$ onto shape $R$.
▶️Answer/Explanation
(a) (i) Rotated $180^{\circ}$ about origin
(ii) Reflected in $y=3$
(iii) Translated by $\left(\begin{array}{r}-5 \\ 3\end{array}\right)$
(b) (i) Reflection
$
x=-1
$
(ii) Enlargement only
(sf) 3
(centre) $(1,3)$
Question
4 (a) Garcia and Elena are each given x dollars.
(i) Elena spends 4 dollars.
Write down an expression in terms of x for the number of dollars she has now.
(ii) Garcia doubles his money by working and then is given another 5 dollars.
Write down an expression in terms of x for the number of dollars he has now.
(iii) Garcia now has three times as much money as Elena.
Write down an equation in x to show this.
(iv) Solve the equation to find the value of x.
(b) Solve the simultaneous equations
$
\begin{array}{r}
3 x-2 y=3, \\
x+4 y=8 .
\end{array}
$
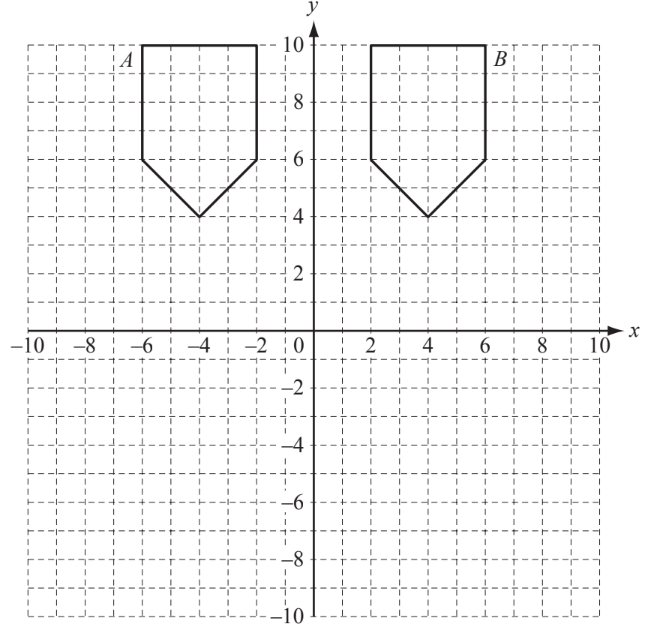
(a) Two different single transformations can map shape A onto shape B.
Describe each transformation fully.
(b) Reflect shape A in the x axis. Draw the image and label it C.
(c) Rotate shape B through 90° clockwise about the origin. Draw the image and label it D.
(d) Describe fully the single transformation which maps shape C onto shape B.
(e) Draw the enlargement of shape $A$, centre $(-4,8)$, with scale factor $\frac{1}{2}$. Label the image $E$.
▶️Answer/Explanation
(a) Reflection in $y$ axis or $x=0$
Translation $\left(\begin{array}{l}8 \\ 0\end{array}\right)$ or 8 right (only)
(b) Correct reflected pentagon
(c) Correct rotated pentagon
(d) Rotation, 180, (About) origin oe
(e) Correct enlarged pentagon
Question

(a) Two different single transformations can map shape A onto shape B.
Describe each transformation fully.
(b) Reflect shape A in the x axis. Draw the image and label it C.
(c) Rotate shape B through 90° clockwise about the origin. Draw the image and label it D.
(d) Describe fully the single transformation which maps shape C onto shape B.
(e) Draw the enlargement of shape $A$, centre $(-4,8)$, with scale factor $\frac{1}{2}$. Label the image $E$.
▶️Answer/Explanation
(a) Reflection in $y$ axis or $x=0$
Translation $\left(\begin{array}{l}8 \\ 0\end{array}\right)$ or 8 right (only)
(b) Correct reflected pentagon
(c) Correct rotated pentagon
(d) Rotation, 180, (About) origin oe
(e) Correct enlarged pentagon
Question
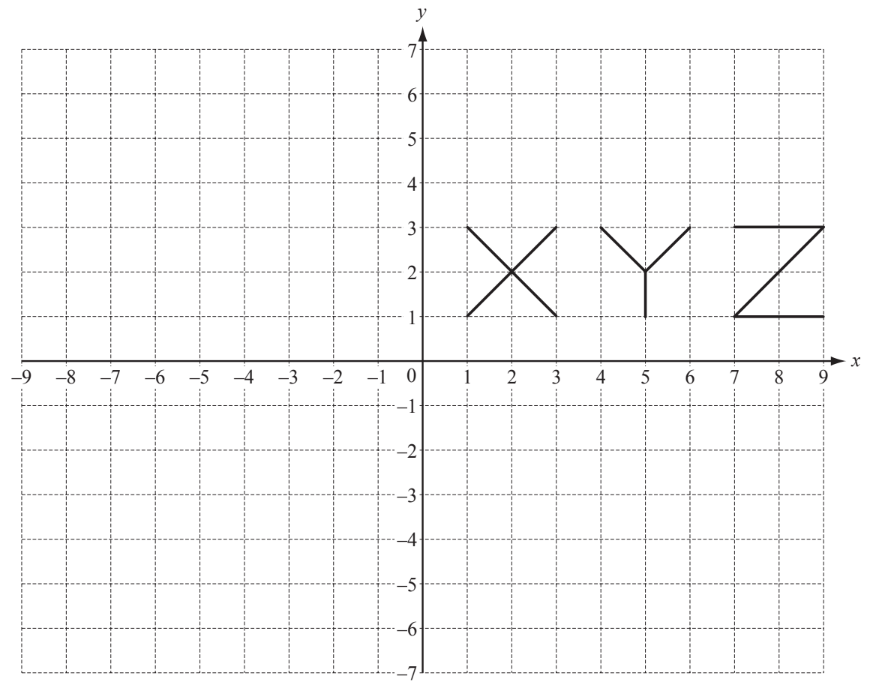
(a) On the grid,
(i) translate $X$ by the vector $\left(\begin{array}{r}-7 \\ 2\end{array}\right)$,
(ii) rotate $Y$ through $90^{\circ}$ anticlockwise about the origin.
(b) (i) On the grid, reflect $Z$ in the $x$-axis. This is the image $Z_1$.
(ii) On the grid, reflect the image $Z_1$ in the line $x=4$. This is the image $Z_2$.
(iii) Describe a single transformation which maps the image $Z_2$ onto the original $Z$.
▶️Answer/Explanation
(a) (i) Correct $\mathrm{X}$
(ii) Correct $Y$
(b) (i) $\operatorname{Correct} Z_1$
(ii) Correct $\mathrm{Z}_2$
(iii) Translation, $\left(\begin{array}{l}8 \\ 4\end{array}\right)$
OR Rotation, through 180 about $(4,0)$
Question
(a) Garcia and Elena are each given x dollars.
(i) Elena spends 4 dollars.
Write down an expression in terms of x for the number of dollars she has now.
(ii) Garcia doubles his money by working and then is given another 5 dollars.
Write down an expression in terms of x for the number of dollars he has now.
(iii) Garcia now has three times as much money as Elena.
Write down an equation in x to show this.
(iv) Solve the equation to find the value of x.
(b) Solve the simultaneous equations
$
\begin{array}{r}
3 x-2 y=3, \\
x+4 y=8 .
\end{array}
$

(a) Two different single transformations can map shape A onto shape B.
Describe each transformation fully.
(b) Reflect shape A in the x axis. Draw the image and label it C.
(c) Rotate shape B through 90° clockwise about the origin. Draw the image and label it D.
(d) Describe fully the single transformation which maps shape C onto shape B.
(e) Draw the enlargement of shape $A$, centre $(-4,8)$, with scale factor $\frac{1}{2}$. Label the image $E$.
▶️Answer/Explanation
(a) Reflection in $y$ axis or $x=0$
Translation $\left(\begin{array}{l}8 \\ 0\end{array}\right)$ or 8 right (only)
(b) Correct reflected pentagon
(c) Correct rotated pentagon
(d) Rotation, 180, (About) origin oe
(e) Correct enlarged pentagon