Question
(a) Bag A contains 20 counters.
6 are red, 9 are blue and the rest are white.
Jared takes one counter at random.
Write down the probability that the counter is
(i) red,
(ii) white,
(iii) yellow.
(b) Bag B contains green counters, black counters, purple counters and brown counters.
Louise takes one counter at random.
Complete the table.
(c) Bag C contains 8 red counters and 12 blue counters only.
Bag D contains 6 red counters and 9 blue counters only.
A counter is taken at random from each bag.
Show that the probability of taking a red counter from bag C is equal to the probability of taking a red
counter from bag D.
Answer/Explanation
Ans:
(a) (i) \(\frac{6}{20}\) oe
(ii) \(\frac{5}{20}\) oe
(iii) 0
(b) [0].28 oe
(c) \(\frac{8}{20}\)
\(\frac{6}{15}\)
Comparing the two fractions
with equal denominators or as
decimals
Question
30 students took a vocabulary test.
The marks they scored are shown below
7 8 5 8 3 2
6 6 3 3 6 2
7 1 5 10 2 6
6 5 8 1 2 7
3 1 5 3 10 3
(a) Complete the frequency table below.
The first five frequencies have been completed for you.
You may use the tally column to help you.
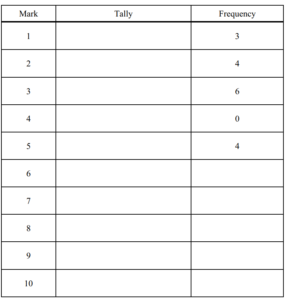
(b) (i) Find the range.
(ii) Write down the mode.
(iii) Find the median.
(iv) Calculate the mean.
(c) A student is chosen at random.
Find the probability that the student scored
(i) 1 mark,
(ii) 4 marks,
(iii) fewer than 6 marks.
Answer/Explanation
(a)

(b)(i) Range= Max marks-Min marks
= 10-1
= 9
(ii) Mode= Max frequency element = 3
(iii) Median
Arrange data in ascending order :
1 1 1 2 2 2 2 3 3 3 3 3 3 5 5 5 5 6 6 6 6 6 6 7 7 7 8 8 8 10
No. of students=30
Therefore, Median =\(\frac{15th+16th element}{2}\)
=\(\frac{5+5}{2}\)
=5
(iv) Mean= \(\frac{3.1+4.2+6.3+0.4+4.5+5.6+3.7+3.8+0.9+2.10}{30}\)
= 4.8
(c)(i) Probability of 1 mark scorer=\(\frac{no. of times 1 mark scored}{total no. of students}\)
= \(\frac{3}{30}\)
=\(\frac{1}{10}\)
(ii) P=\(\frac{0}{30}\)
(iii) Sum of probabilities :
\(\frac{4}{30}+\frac{0}{30}+\frac{6}{30}+\frac{4}{30}+\frac{3}{30}\)=\(\frac{17}{30}\)
