Question
The Patel family flies from their home town, H, to Kiruna, K, in Lapland.
(a) The scale drawing shows their journey.
The scale is 1 centimetre represents 40 kilometres.
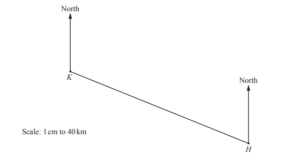
(i) Measure the bearing of K from H.
Answer/Explanation
Ans: 292
(ii) Work out the distance in kilometres from H to K.
Answer/Explanation
Ans: 380 km
(iii) The average speed of the plane is 450km/h.
Find the average speed in m/s.
Answer/Explanation
Ans: 125 m/s
(b) The probability that the plane arrives on time is 0.15 .
(i) Write down the probability that the plane does not arrive on time.
Answer/Explanation
Ans: 0.85
(ii) Every year there are 240 flights from H to K.
Calculate the expected number of flights that arrive on time.
Answer/Explanation
Ans: 36
(c) The Patel family has six suitcases.
The number of items in each suitcase is shown below.
15 16 16 18 19 21
(i) Find the range.
Answer/Explanation
Ans: 6
(ii) Write down the mode.
Answer/Explanation
Ans: 16
(iii) Work out the median.
Answer/Explanation
Ans: 17
(iv) Calculate the mean.
Answer/Explanation
Ans: 17.5
(v) Find the probability that a suitcase chosen at random has more than 18 items.
Answer/Explanation
Ans: \(\frac{2}{6}oe\)
(d) Mr Patel buys a bag of sweets.
The bag of sweets costs $3.25 .
(i) Calculate the cost of the sweets in euros (€) when the exchange rate is €1 = $1.24 .
Answer/Explanation
Ans: 2.62
(ii) The weight, w grams, of the bag of sweets is 250g correct to the nearest 10 g.
Complete this statement about the value of w.
Answer/Explanation
Ans: 245 ≤ w < 255
Question
Olga owns a fruit and vegetable shop.
(a) An apple weighs 70 g correct to the nearest 5g.
Complete the statement about the mass, m grams, of this apple.
Answer/Explanation
Ans: 67.5
72.5
(b) The number of strawberries in each of 12 boxes is shown below.
23 21 21 20 21 20
22 22 21 20 20 20
(i) Find the range.
Answer/Explanation
Ans: 3
(ii) Write down the mode.
Answer/Explanation
Ans: 20
(iii) Find the median.
Answer/Explanation
Ans: 21
(iv) Calculate the mean.
Answer/Explanation
Ans: 20.9 or 20.91 to 20.92
(v) Find the probability that a box chosen at random has 22 or 23 strawberries in the box.
Answer/Explanation
Ans: \(\frac{3}{12}oe\)
(c) The shop sells potatoes in bags A, B and C.
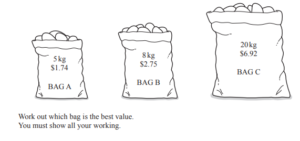
Answer/Explanation
Ans: complete correct method shown and Bag B oe
(d) The price of plums is $2.40 per kilogram.
Olga reduces this price by 35%.
Calculate the new price per kilogram.
Answer/Explanation
Ans: $ 1.56
Question
Javier went to a carnival with his friends.
(a) He played five games of darts.
These are his scores.
160 58 45 82 125
(i) Work out his mean score.
(ii) Find the range.
(b) The 5000 tickets for the carnival are different colours.
The table shows the number of tickets of each colour.
| Colour of ticket | Red | Green | Blue | Pink | White |
| Number of tickets | 370 | 560 | 1800 | 1320 | 950 |
A ticket is picked at random.
Find the probability that this ticket is Blue.
(c) Five different types of food are sold at the carnival.
Javier chooses one of these types of food.
The table shows the probability that he chooses each type of food.
| Type of food | Curry | Fries | Pasta | Burger | Salad |
| Probability | 0.15 | 0.23 | 0.4 | 0.07 |
Complete the table.
(d) Javier hires a four-seater bike.
The hire cost is $8.50 for the first hour and then $7.75 for each extra hour.
Calculate the cost of hiring the bike for 5 hours.
$ …………………………………………
(e) The table shows the number of drinks sold by one stall at the carnival.
| Drink | Number sold |
| Tea | 70 |
| Orange | 60 |
| Water | 120 |
| Coffee | 180 |
| Smoothie | 40 |
Draw a bar chart to show this information.
Complete the scale on the frequency axis.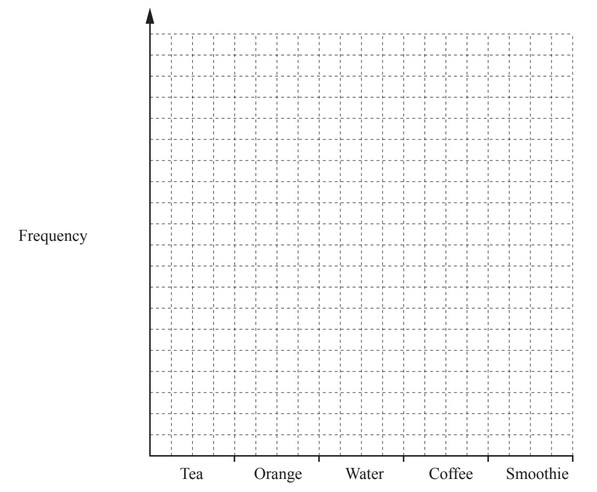
Answer/Explanation
Answer:
(a) (i) 94
(ii) 115
(b) \(\frac{1800}{5000}\) oe isw
(c) [0].15
(d) 39.5[0]
(e) Correct bar chart
Question
(a) Bag A contains 20 counters.
6 are red, 9 are blue and the rest are white.
Jared takes one counter at random.
Write down the probability that the counter is
(i) red,
(ii) white,
(iii) yellow.
(b) Bag B contains green counters, black counters, purple counters and brown counters.
Louise takes one counter at random.
Complete the table.
(c) Bag C contains 8 red counters and 12 blue counters only.
Bag D contains 6 red counters and 9 blue counters only.
A counter is taken at random from each bag.
Show that the probability of taking a red counter from bag C is equal to the probability of taking a red
counter from bag D.
Answer/Explanation
Ans:
(a) (i) \(\frac{6}{20}\) oe
(ii) \(\frac{5}{20}\) oe
(iii) 0
(b) [0].28 oe
(c) \(\frac{8}{20}\)
\(\frac{6}{15}\)
Comparing the two fractions
with equal denominators or as
decimals
Question
(a) The scale drawing shows the positions of two buoys, A and B, in the sea.
The scale is 1 centimeter represents 20 kilometers.
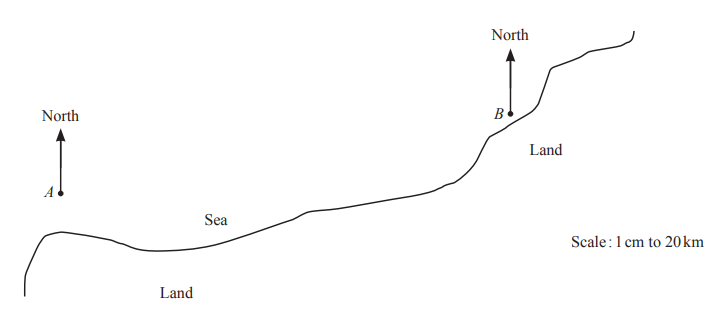
(i) Work out the actual distance between buoy A and buoy B.
km [2]
(ii) Measure the bearing of buoy B from buoy A.[1]
(iii) Buoy C is 120 km from buoy B on a bearing of 300°.
On the scale drawing, mark the position of buoy C. [2]
(iv) Marco sails his boat so that he is always equidistant from buoy A and buoy B.
On the scale drawing, use a straight edge and compasses only to construct the path of the boat. Show all your construction arcs. [2]
(b) The amount of fuel, t liters, in the boat’s fuel tank is 135 liters, correct to the nearest liter.
Complete the statement about the value of t.
____ \(\leqslant t< \) ____ [2]
(c) Marco has ropes of four different colours.
He takes a rope at random.

Complete the table. [2]
(d) When Marco arrives at a port the temperature is 5°C.
At midnight the temperature has fallen by 7°C.
Find the temperature at midnight.
°C [1]
(e) Last year the cost to keep a boat at the port was \($\)14 per night.
This year the cost has increased by 12%.
Calculate the cost this year.
\($\)[2]
(f) Marco watched 25 boats enter the port, of which 9 had a mast.
There are a total of 200 boats in the port.
Calculate an estimate of the number of boats in the port that have a mast.[2]
Answer/Explanation
Ans:
8(a)(i) 220
8(a)(ii) [0]80°
8(a)(iii) C in correct position
8(a)(iv) Correct line drawn with 2 pairs of correct arcs
8(b) 134.5, 135.5
8(c) 0.41
8(d) –2
8(e) 15.68 cao
8(f) 72
Question
(a)
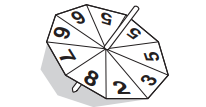
The diagram shows a fair 9-sided spinner.
The numbers on the spinner are 2, 3, 5, 5, 5, 6, 6, 7 and 8.
(i) The spinner is spun once.
Write down the probability that the spinner lands on
(a) the number 8,
Answer/Explanation
Ans: \(\frac{1}{9}oe\)
(b) a number less than 7.
Answer/Explanation
Ans: \(\frac{7}{9}oe\)
(ii) The spinner is spun 135 times.
Work out the expected number of times the spinner lands on the number 6.
Answer/Explanation
Ans: 30
(b) Hitesh throws a dice 80 times.
The results are shown in the table.
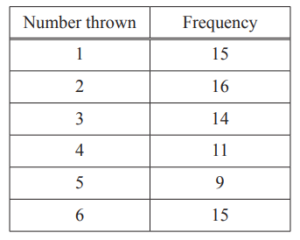
(i) Write down the mode.
Answer/Explanation
Ans: 2
(ii) Work out the range.
Answer/Explanation
Ans: 5
(iii) Work out the median.
Answer/Explanation
Ans: 3
(iv) Calculate the mean.
Answer/Explanation
Ans: 3.35
Question
(a) Jian has a fair spinner in the shape of a regular hexagon.
The spinner is numbered 2, 2, 3, 4, 4, 5.
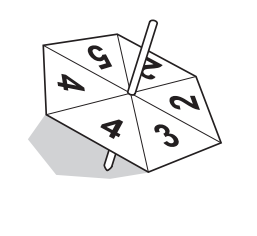
Jian spins the spinner.
Find the probability that the spinner lands on
(i) an even number,
………………………………………….
(ii) a number less than 6,
………………………………………….
(iii) the number 1
(b) Mei has two fair square spinners, A and B.
Spinner A is numbered 1, 2, 2, 4 and spinner B is numbered 3, 3, 4, 5.
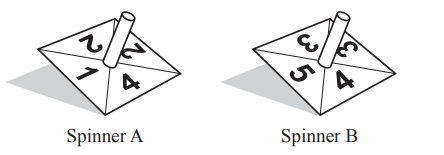
She spins both spinners and adds the two numbers.
(i) Complete the table to show all the possible outcomes.
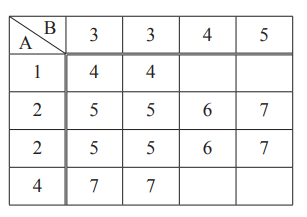
(ii) Use the table to write down the probability that the total is
(a) 5,
………………………………………….
(b) more than 5.
………………………………………….
(c) Ning has a spinner numbered 1 to 6.
She spins it 50 times and her results are shown in the table.
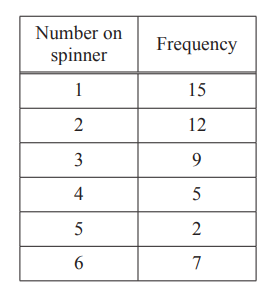
(i) Write down the mode.
………………………………………….
(ii) Find the median.
………………………………………….
(iii) Work out the mean.
………………………………………….
Answer/Explanation
(a)(i)\(\frac{2}{3}\)
(ii) 1
(iii) 0
(b)(i) 5 6
8 9
in the correct places
(ii)(a)\( \frac{5}{16}\)
(b) \(\frac{9}{16}\)
(c)(i) 1
(ii) 2
(iii) 2.76
Question
(a) One day, Mahika records the number of teachers and students who cycle to school.
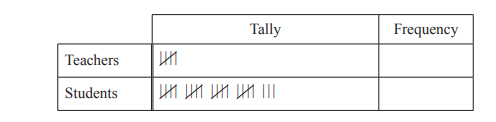
(i) Complete the frequency column in the table.
Answer/Explanation
Ans: 5 23
(ii) Work out the percentage of people who cycle that are students.
Answer/Explanation
Ans: 82.1 or 82.14…
(b) Mahika records how 120 students from Year 1 and Year 2 travel to school.
Each student walks, cycles or travels by bus.
• 48 students are in Year 1.
• 77 students walk.
• 5 students in Year 2 cycle.
• 36 students travel by bus.
• \(\frac{4}{9}\) of the students who travel by bus are in Year 1.
(i) Complete the table.
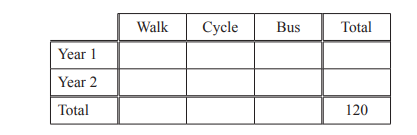
Answer/Explanation
Ans: 30 2 16 48
47 5 20 72
77 7 36 [120]
(ii) One of the 120 students is chosen at random.
Work out the probability that this student does not travel by bus to school.
Answer/Explanation
Ans: \(\frac{7}{10}oe\)
(c) There have been 24 complaints about one of the buses.
The complaints are:
• The bus is late.
• The price is too high.
• The bus is crowded.
(i) Complete the table.
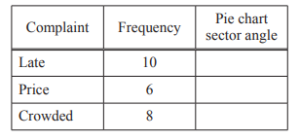
Answer/Explanation
Ans: 150, 90, 120
(ii) Complete the pie chart.
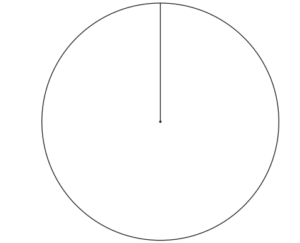
Answer/Explanation
Ans: Correct pie chart drawn
Question
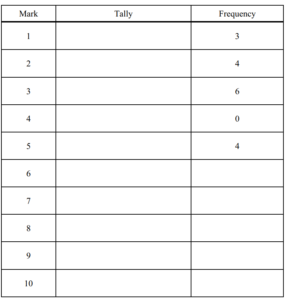
30 students took a vocabulary test.
The marks they scored are shown below
7 8 5 8 3 2
6 6 3 3 6 2
7 1 5 10 2 6
6 5 8 1 2 7
3 1 5 3 10 3
(a) Complete the frequency table below.
The first five frequencies have been completed for you.
You may use the tally column to help you.
(b) (i) Find the range.
(ii) Write down the mode.
(iii) Find the median.
(iv) Calculate the mean.
(c) A student is chosen at random.
Find the probability that the student scored
(i) 1 mark,
(ii) 4 marks,
(iii) fewer than 6 marks.
Answer/Explanation
(a)

(b)(i) Range= Max marks-Min marks
= 10-1
= 9
(ii) Mode= Max frequency element = 3
(iii) Median
Arrange data in ascending order :
1 1 1 2 2 2 2 3 3 3 3 3 3 5 5 5 5 6 6 6 6 6 6 7 7 7 8 8 8 10
No. of students=30
Therefore, Median =\(\frac{15th+16th element}{2}\)
=\(\frac{5+5}{2}\)
=5
(iv) Mean= \(\frac{3.1+4.2+6.3+0.4+4.5+5.6+3.7+3.8+0.9+2.10}{30}\)
= 4.8
(c)(i) Probability of 1 mark scorer=\(\frac{no. of times 1 mark scored}{total no. of students}\)
= \(\frac{3}{30}\)
=\(\frac{1}{10}\)
(ii) P=\(\frac{0}{30}\)
(iii) Sum of probabilities :
\(\frac{4}{30}+\frac{0}{30}+\frac{6}{30}+\frac{4}{30}+\frac{3}{30}\)=\(\frac{17}{30}\)
Question
36 29 41 45 15 10 13
Use the numbers in the list above to answer all the following questions.
(a) Write down
(i) two even numbers,
(ii) two prime numbers,
(iii) a square number,
(iv) two factors of 90 .
(b) (i) Calculate the mean of the seven numbers
(ii) Find the median.
(iii) Find the range.
(c) A number from the list is chosen at random.
Find the probability that the number is
(i) even,
(ii) a multiple of 5
Answer/Explanation
(a) (i) 36,10
(ii) 29,41
(iii) 36=\(6^2\)
(iv) 45,10
(b)(i) Mean=\(\frac{Sum of total numbers}{Total number}\)
Mean =\(\frac{36 + 29 + 41 + 45 + 15 + 10 + 13}{7} = \frac{189}{7}\)
=27
(ii) To find the median, we first need to arrange the numbers in order:
10, 13, 15, 29, 36, 41, 45
Since, there are odd number of numbers, so the median is the middle number
Median = 29
(iii)Range= Largest number- Smallest number
=45 – 10
= 35
(c) The total number of elements in the list is 7.
(i) The even numbers in the list are 36, 10.
P(even) = \(\frac{Number of even numbers}{Total number of elements}
= \(\frac{2}{7}\)
Therefore, the probability of choosing an even number at random from the list is approximately 0.286
(ii) The multiples of 5 in the list are: 45, 15, 10.
P(multiple of 5) = \(\frac{Number of multiples of 5}{Total number of elements}\)
\(\frac{3}{7}\)
Question
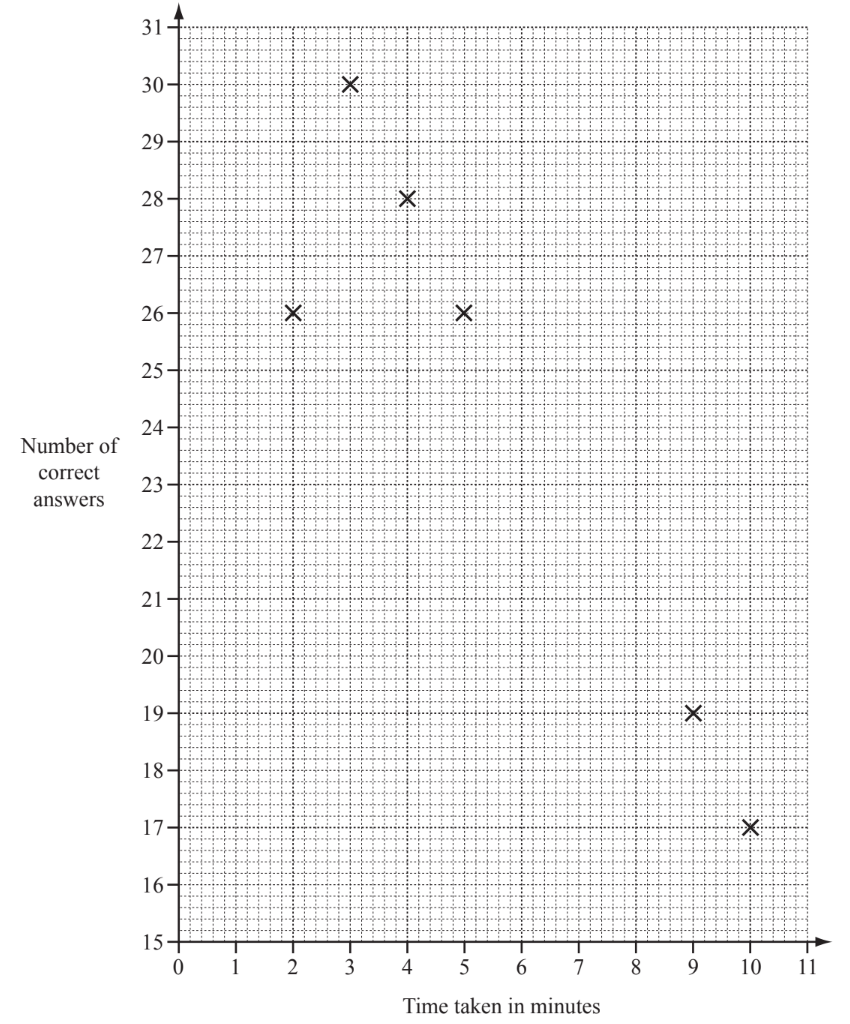
Twelve students each answer 30 questions in a quiz.
The time taken and the number of correct answers for each student is given in the table.

(a) Complete the scatter diagram below to show this information. The first six points have been plotted for you.
(b) What type of correlation does the scatter diagram show?
(c) (i) Find the range of the time taken.
(ii) Calculate the mean time taken.
(d) (i) Find the mode for the number of correct answers.
(ii) Find the median for the number of correct answers.
(e) One of the 12 students is selected at random. Write down the probability that the student
(i) took more than 8 minutes to answer the quiz,
(ii) took less than 5 minutes and had more than 24 correct answers.
▶️Answer/Explanation
(a) 6 points correctly plotted
(b) negative cao
(c) (i) $8 \mathrm{cao}$
(ii) $\operatorname{art} 5.92$
(d) (i) $26 \mathrm{cao}$
(ii) 23.5 cao
(e) (i) $\frac{2}{12}$ oe
(ii) $\frac{3}{12}$ oe
Question
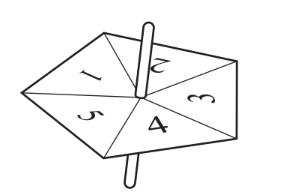
Jonah uses a fair five-sided spinner in a game.
(a) What is the probability that the spinner lands on
(i) 3 ,
(ii) an even number,
(b) Jonah spins the spinner 25 times and records the results in a frequency table.
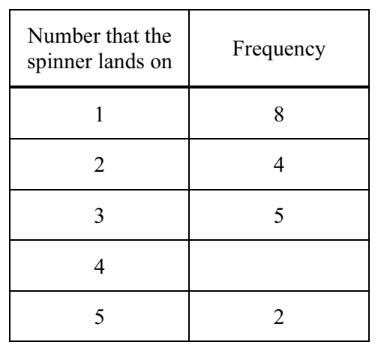
(i) Fill in the missing number.
(ii) Write down the mode.
(iii) Calculate the mean.
(iv) On the grid, draw a bar chart to show these results.
▶️Answer/Explanation
(a) (i) $1 / 5$
(ii) $2 / 5$
(iii) 0
(b) (i) 6
(ii) 1
(iii) $2.6(0) \mathrm{www}$
(iv) heights $8,4,5,2$ 6 or $\mathrm{ft}$ height for their (b) (i)
