Question

The table shows the average temperature for Tromso, Norway each month.
(a) (i) Write down the month which had the highest average temperature.
(ii) How much warmer was it in September than in February?
(iii) The lowest temperature in October was 12.3°C below the average temperature for that
month.
Work out the lowest temperature in October.
(b) In a survey, some tourists were asked how they had travelled to Norway.
The pie chart shows the results.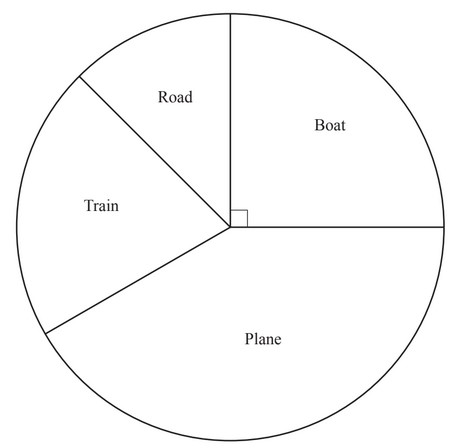
(i) 150 of these tourists travelled by boat.
Show that 600 tourists took part in the survey.
(ii) Calculate the number of these tourists who travelled by plane.
(c) A train ticket from Oslo to Stavanger costs 885 krone.
There is a discount of 12% on the total cost of the tickets for a group of 10 or more people.
Calculate the cost of tickets for a group of 15 people.
(d) On 1 January 2000, the population of Norway was 4480 000, correct to 3 signifi cant fi gures.
(i) Write this number in standard form.
(ii) On 1 January 2011, the population of Norway was 4920000, correct to 3 signifi cant fi gures.
Calculate the percentage increase in the population.
Answer/Explanation
Answer:
(a) (i) July or Jul
(ii) 10.9
(iii) -9.6
(b) (i) \(150 \div \frac{90}{360}\) oe
(ii) 250
(c) 11682
(d) (i) \(4.48 \times 10^6\) cao
(ii) 9.82
Question
The table shows a summary of the types of employment for 90 people.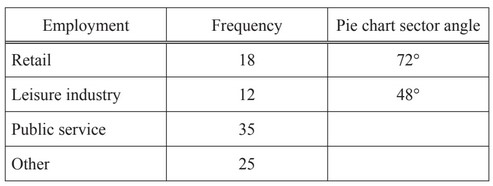
(a) (i) Complete the table.
(ii) Complete the pie chart and label the sectors.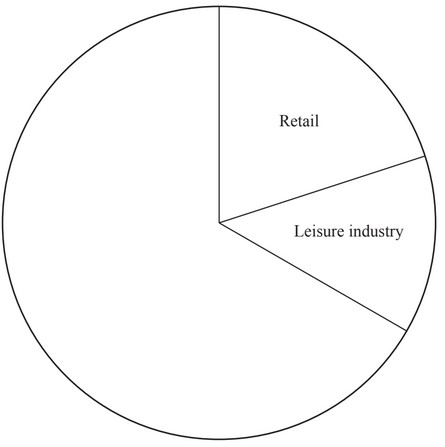
(b) Here are the ages of the people working in the leisure industry.
16 17 19 23 23 24 27 31 33 40 45 56
(i) Work out the range.
(ii) Calculate the mean.
(iii) Sabrina wants to interview someone working in the leisure industry.
She chooses one person at random.
Write down the probability that the person chosen is under 30 years old.
Answer/Explanation
Answer:
(a) (i) 140
(ii) 100
(ii) correct labelled pie chart
(b) (i) 40
(ii) 29.5
(iii) \(\frac{7}{12}\) oe
Question
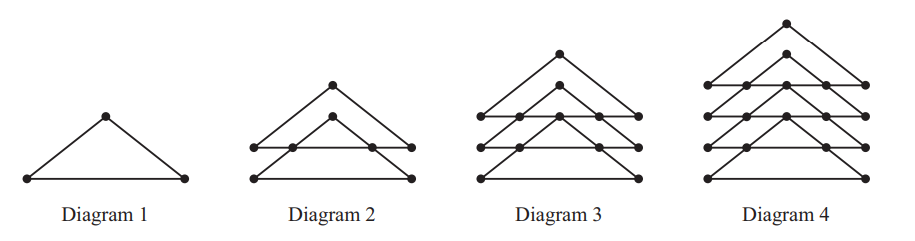
Diagrams 1 to 4 show a sequence of shapes made up of lines and dots at the intersections of lines.
(a) (i) Complete the table showing the number of dots in each diagram.
| Diagram | 1 | 2 | 3 | 4 | 5 | 6 |
| Dots | 3 | 8 | 13 |
Answer/Explanation
Ans:
| Diagram | 1 | 2 | 3 | 4 | 5 | 6 |
| Dots | 3 | 8 | 13 | 18 | 23 | 28 |
(ii) Write down the rule for continuing the sequence of dots.
Answer/Explanation
Ans: Add 5 oe
(iii) Write down an expression, in terms of n, for the number of dots in Diagram n.
Answer/Explanation
Ans: 5n – 2 oe
(iv) Find the number of dots in Diagram 15.
Answer/Explanation
Ans: 73
(b) The dots are joined by sloping lines and horizontal lines.
(i) Diagram 1 has 2 sloping lines and Diagram 2 has 6 sloping lines.
Find the number of sloping lines in Diagrams 3 and 4.
Answer/Explanation
Ans: 10 14
(ii) Write down an expression, in terms of n, for the number of sloping lines in Diagram n.
Answer/Explanation
Ans: 4n – 2 oe
Question
(a) One day a survey is taken of the ages of 120 children at a fairground.
The results are shown in the frequency table.
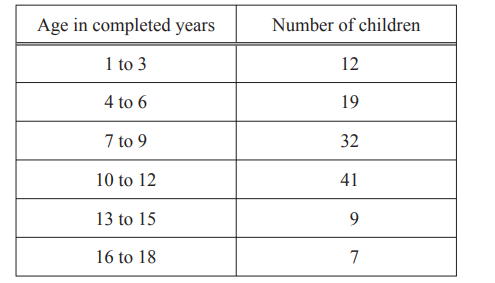
(i) On the grid, draw a bar chart for this data.
Complete the scale on the frequency axis.
Answer/Explanation
Ans: Correct diagram with scale
(ii) What is the modal age group?
Answer/Explanation
Ans: 10 to 12 cao
(iii) One of the 120 children is chosen at random.
Write down the probability that the child is aged 4 to 6.
Answer/Explanation
Ans: \(\frac{19}{120}\) or 0.158[3….] or 15.8[3……]%
(b) Lalia says the probability of taking a yellow bead from a bag containing yellow beads and black beads is \(\frac{7}{5}.\)
Explain why \(\frac{7}{5}\) cannot be a correct probability
Answer/Explanation
Ans: Probability must be between 0 and 1 oe
(c) Another bag contains 9 green marbles and 11 red marbles.
A marble is taken at random.
Write down the probability that the marble is
(i) green,
Answer/Explanation
Ans: \(\frac{9}{20}\) or 0.45 or 45%
(ii) blue.
Answer/Explanation
Ans: 0 oe
Question
120 people are asked how they travel to work.
The pie chart shows the results.
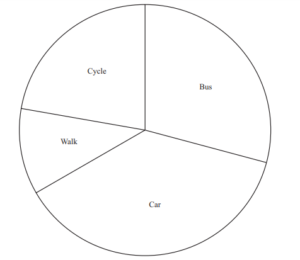
(a) (i) Show that 45 people travel by car.
Answer/Explanation
Ans: [Car angle =] 135 (± 2°)
135 ÷ 360 × 120 ( = 45 )
(ii) A person is chosen at random from the 120 people.
Find the probability that this person travels to work by bus or by car
Answer/Explanation
Ans: 2/3 or value from 0.658 to 0.675
(b) One year later, the same 120 people were again asked how they travel to work.
Here is the information.

(i) Use this information to complete the following equation, in terms of x.
………………………………………………………………………………… = 120
Answer/Explanation
Ans: x + 31 + x + 17 + 2x [= 120] or better
(ii) Solve the equation to fi nd the number of people who walk to work.
Answer/Explanation
Ans: 18 cao
Question
Denzil grows tomatoes. He selects a random sample of 25 tomatoes.
The mass of each tomato, to the nearest 5 grams, is shown below.
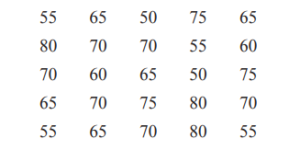
(a) (i) Complete the frequency table.
You may use the tally column to help you.
| Mass (grams) | Tally | Frequency |
| 50 | ||
| 55 | ||
| 60 | ||
| 65 | ||
| 70 | ||
| 75 | ||
| 80 |
Answer/Explanation
Ans:
| Mass (grams) | Tally | Frequency |
| 50 | 2 | |
| 55 | 2 | |
| 60 | 4 | |
| 65 | 5 | |
| 70 | 6 | |
| 75 | 3 | |
| 80 | 3 |
(ii) Write down the mode.
Answer/Explanation
Ans: 70
(iii) Find the range.
Answer/Explanation
Ans: 30
(iv) Show that the mean mass is 66g
Answer/Explanation
Ans: ∑(Frequency, f × mass, w)
1650 ÷ 25
(b) Denzil picks 800 tomatoes.
4% of the 800 tomatoes are damaged.
How many of these tomatoes are not damaged?
Answer/Explanation
Ans: 768
(c) Denzil sells 750 of his tomatoes.
(i) The mean mass of a tomato is 66g.
Calculate the mass of the 750 tomatoes in kilograms.
Answer/Explanation
Ans: 49.5 cao
(ii) Denzil sells his tomatoes at $1.40 per kilogram.
Calculate the total amount he receives from selling all the 750 tomatoes.
Answer/Explanation
Ans: 69.3[0]
(iii) The cost of growing these tomatoes was $33.
Calculate his percentage profi t.
Answer/Explanation
Ans: 110
Question
(a) The scatter diagram shows the scores for each student in class A for the written test and the speaking
test in French.
A line of best fit has been drawn.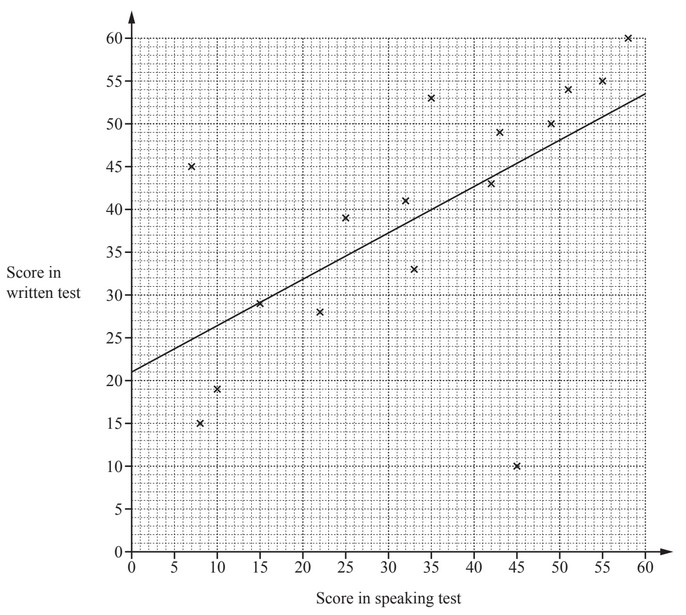
(i) Each test is marked out of 60.
In which test did the class perform better?
Give a reason for your answer.
………………………………………. because ……………………………………………………………………………..
(ii) What type of correlation is shown in the scatter diagram?
(iii) One student is much better at speaking French than writing French.
Put a ring around the cross that represents this student.
(iv) One student scored 39 in the speaking test but was absent for the written test.
Use the line of best fit to estimate a score for this student in the written test.
(b) Here are the scores in the written test for class B.
21 14 48 32 8 29 41 39 30 23 17
Find
(i) the median,
(ii) the mean.
Answer/Explanation
Ans:
(a) (i) Written test and a valid reason
(ii) Positive
(iii) (45,10) indicated
(iv) 42
(b) (i) 29
(ii) 27.5 or 27.45 to 27.46
Question
(a) 25 students go on a water sports trip.
The students each choose their favourite water sport.
These are the results.

(i) Complete the frequency table for the results.
You may use the tally column to help you.
(ii) Write down the mode.
…………………………………………
(iii) Work out the percentage of students whose favourite water sport is snorkelling.
…………………………………….. %
(b) The table shows the times of the high and low tides.
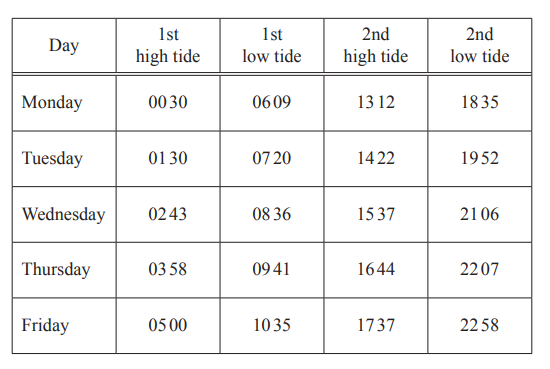
(i) Write down the time of the 2nd high tide on Wednesday using the 12-hour clock.
…………………………………………
(ii) Work out the time between the two low tides on Thursday.
………….. h ………….. min
(iii) The surfing activity starts \(1\frac{1}{2}\) hours before the high tide on Tuesday afternoon.
Write down the time that the surfing activity starts.
…………………………………………
Answer/Explanation
(a)(i)5, 8, 4, 2, 6
(ii)Surfing
(b)(i)3.37pm
(ii)12h 26min
(iii)12:52pm
Question
(a) Each of 196 candidates has a candidate number from 3001 to 3196.
The candidates sit in numerical order in columns and rows, as shown in the diagram.
There are 20 rows.
The diagram shows part of the plan for where the candidates sit
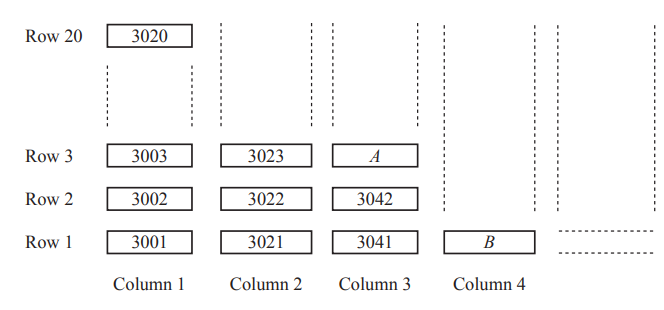
(i) The diagram shows where candidates A and B sit.
Write down their numbers.
A ………………………………………….
B . …………………………………………
(ii) Complete this statement.
Candidate 3135 sits in Column …………………….. , Row ……………………..
(iii) Candidate C sits in Column n, Row 1.
Find an expression, in terms of n, for the number of candidate C.
…………………………………………
(b)The geography examination lasts for 1 hour 40 minutes.
Hari is allowed 25% extra time for his geography examination.
Work out the total time Hari has for this examination.
Give your answer in hours and minutes.
………….. h ………….. min
(c) The number of examinations that each of the 196 candidates takes is recorded in the table.
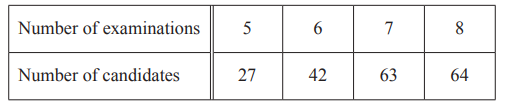
(i) Write down the range.
…………………………………………
(ii) Find the median.
…………………………………………
(iii) Calculate the mean.
…………………………………………
(iv) A candidate is selected at random. Find the probability that the candidate takes fewer than 8 examinations.
…………………………………………
Answer/Explanation
a(i)3043
3061
(ii)Column 7 Row 15
(iii) 20n + 2981
(b)2[h] 5[min]
(c)(i)3
(ii)7
(iii)6.84 or 6.836 to 6.837 or \(6\frac{41}{49}\)
(iv)\(\frac{132}{196}\)
Question
Mrs. Verma has a restaurant.
In the restaurant each table has 8 chairs.
Sometimes she puts tables together.
The diagrams show how the tables are put together and the position of each chair (X).
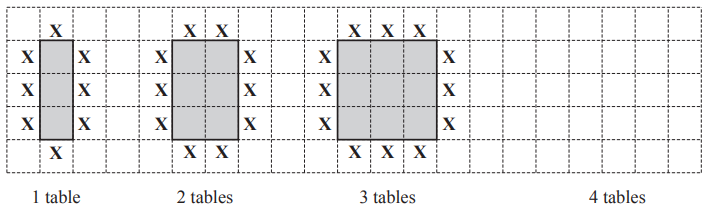
The pattern of tables and chairs forms a sequence.
(a) Draw the diagram for 4 tables. [1]
(b) Complete the table. [2]
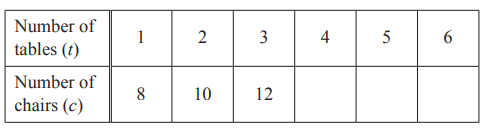
(c) Find a formula for the number of chairs, c, in terms of the number of tables, t.
c = [2]
(d) 18 tables are put together in this way.
Work out the number of chairs needed.[2]
(e) Work out the number of tables, put together in this way, when 80 chairs are needed.[2]
Answer/Explanation
Ans:
5(a) 4 tables and 14 chairs correctly drawn
5(b) 14, 16, 18
5(c) 2 6 t + oe final answer
5(d) 42 cao
5(e) 37 cao
Question
(a) Jon spins this 6-sided spinner.
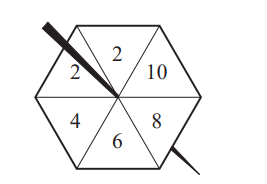
The probability that the spinner lands on any of the six sides is equally likely.
Write down the probability that the spinner lands on
(i) the number 6,
Answer/Explanation
Ans: \(\frac{1}{6}oe\)
(ii) a prime number,
Answer/Explanation
Ans: \(\frac{2}{6}oe\)
(iii) a number less than 11.
Answer/Explanation
Ans: 1
(b) Felix has a 12-sided spinner with the numbers 2, 4, 5, 7 and 9 written on it.
It is equally likely to land on any side.
The table shows the probability of the spinner landing on each number.

The diagram of the spinner has been completed for the number 2.
Complete the diagram for the numbers 4, 5, 7 and 9.
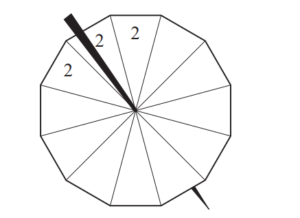
Answer/Explanation
Ans: (2,2,2), 4,4,4,4,5,5,7,7,9 seen on spinner
(c) Felix says that his spinner is more likely to land on a 2 than Jon’s spinner.
Explain why he is wrong.
Answer/Explanation
Ans: Felix’s probability is \(\frac{3}{12}\) which is
less than Jon’s probability \(\left (of\frac{2}{6} \right )\) which is \(\frac{4}{12}oe\)
(d) Felix spins his 12-sided spinner 60 times and records the results.
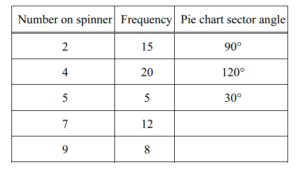
(i) Complete the table by working out the sector angles for the numbers 7 and 9 .
Answer/Explanation
Ans: (90°, 120°, 30°), 72°, 48°
(ii) Complete the pie chart.
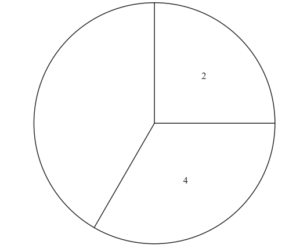
Answer/Explanation
Ans: 30° angle correct 72°, 48°
(iii) Write down the mode.
Answer/Explanation
Ans: 4
(iv) Calculate the mean.
Answer/Explanation
Ans: 4.85
Question
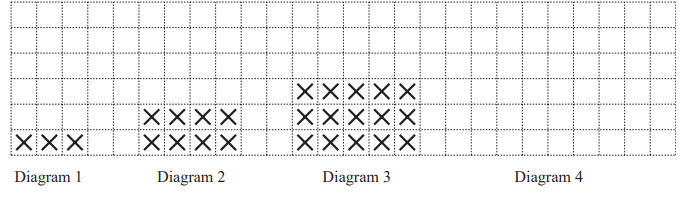
The number of crosses in each Diagram forms a sequence.
(a) On the grid draw Diagram 4.
Answer/Explanation
Ans: Correct diagram: 4 rows & 6 columns
(b) Write down the number of crosses needed to draw Diagram 5.
Answer/Explanation
Ans: 35
(c) Diagram 1 has 1 row of 3 crosses.
Diagram 2 has 2 rows of 4 crosses.
(i) Complete this statement for Diagram n.
Diagram n has n rows of crosses.
Answer/Explanation
Ans: n + 2 cao
(ii) Write down, in terms of n, how many crosses are needed to draw Diagram n.
Answer/Explanation
Ans: n (n + 2) oe
(iii) Find the number of crosses needed to draw Diagram 20.
Answer/Explanation
Ans: 440
Question
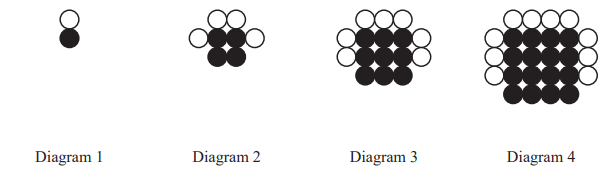
A sequence of diagrams is made from black counters and white counters.
The first four diagrams in the sequence are shown.
(a) Complete the table.
Answer/Explanation
Ans: 9 16 25
7 10 13
(b) Complete the statement.
The numbers of black counters are all numbers.
Answer/Explanation
Ans: square
(c) How many white counters are needed for
(i) Diagram 8,
Answer/Explanation
Ans: 22
(ii) Diagram n?
Answer/Explanation
Ans: 3n – 2 oe final answer
(d) Diagram p contains 58 white counters.
(i) Find the value of p.
Answer/Explanation
Ans: 20
(ii) Find the number of black counters in Diagram p.
Answer/Explanation
Ans: 400
Question
30 students took a vocabulary test.
The marks they scored are shown below
7 8 5 8 3 2
6 6 3 3 6 2
7 1 5 10 2 6
6 5 8 1 2 7
3 1 5 3 10 3
(a) Complete the frequency table below.
The first five frequencies have been completed for you.
You may use the tally column to help you.
(b) (i) Find the range.
(ii) Write down the mode.
(iii) Find the median.
(iv) Calculate the mean.
(c) A student is chosen at random.
Find the probability that the student scored
(i) 1 mark,
(ii) 4 marks,
(iii) fewer than 6 marks.
Answer/Explanation
(a)

(b)(i) Range= Max marks-Min marks
= 10-1
= 9
(ii) Mode= Max frequency element = 3
(iii) Median
Arrange data in ascending order :
1 1 1 2 2 2 2 3 3 3 3 3 3 5 5 5 5 6 6 6 6 6 6 7 7 7 8 8 8 10
No. of students=30
Therefore, Median =\(\frac{15th+16th element}{2}\)
=\(\frac{5+5}{2}\)
=5
(iv) Mean= \(\frac{3.1+4.2+6.3+0.4+4.5+5.6+3.7+3.8+0.9+2.10}{30}\)
= 4.8
(c)(i) Probability of 1 mark scorer=\(\frac{no. of times 1 mark scored}{total no. of students}\)
= \(\frac{3}{30}\)
=\(\frac{1}{10}\)
(ii) P=\(\frac{0}{30}\)
(iii) Sum of probabilities :
\(\frac{4}{30}+\frac{0}{30}+\frac{6}{30}+\frac{4}{30}+\frac{3}{30}\)=\(\frac{17}{30}\)
Question
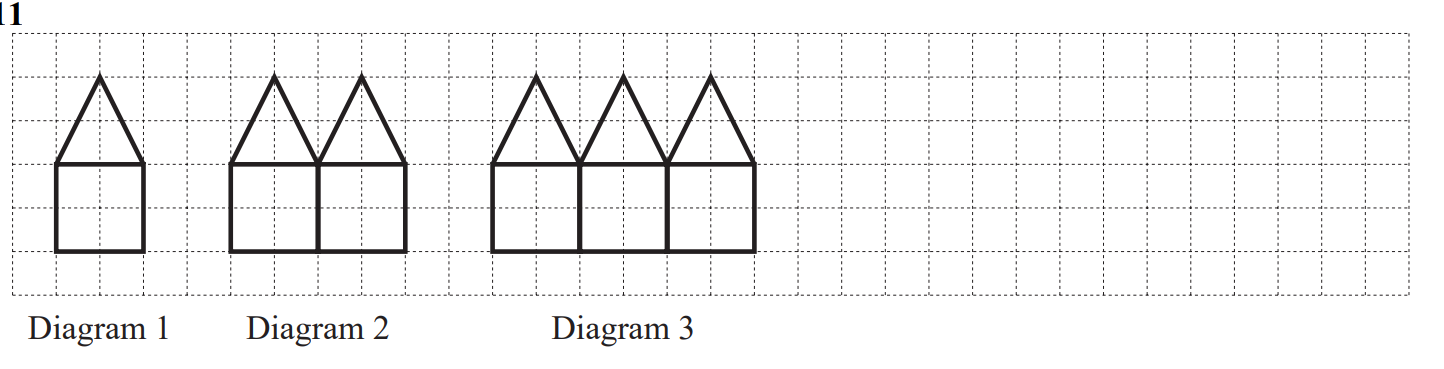
The diagrams show a sequence of shapes.
(a) On the grid, draw Diagram 4.
(b) Complete the table showing the number of lines in each diagram.
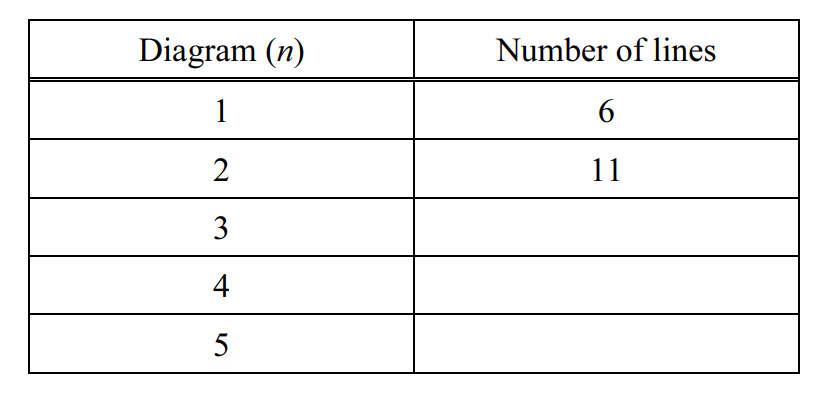
(c) Work out the number of lines in Diagram 8.
(d) Write down an expression, in terms of n, for the number of lines in Diagram n.
(e) Work out the number of lines in Diagram 100
(f) The number of lines in Diagram p is 66.
Find the value of p.
Answer/Explanation
(a) 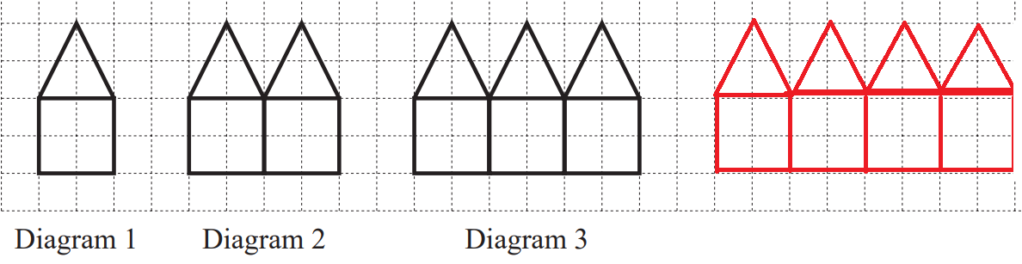
(b) 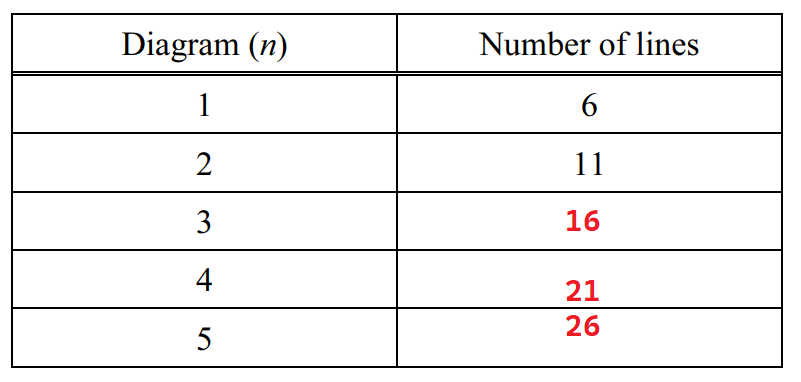
(c) 48-7=41
(d) \(6 \times n-(n-1)\)
= 6n-n+1
= 5n+1
(e) \(500\times 100+1\)(5n+1)
=501
(f) 5n+1= no. of lines in diagram n
5p+1 = 66
5p= 65
p=13
Question
Here is a sequence of diagrams made using identical rectangles.
A dot is shown at the junction of three lines.
A cross is shown at the junction of two lines.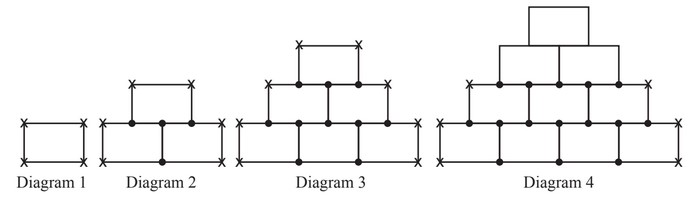
(a) Write down the order of rotational symmetry of Diagram 1.
(b) Complete Diagram 4 using dots and crosses.
(c) Complete the table for Diagram 4 and Diagram 5.
| Diagram | 1 | 2 | 3 | 4 | 5 |
| Number of dots | 0 | 4 | 10 | ||
| Number of crosses | 4 | 6 | 8 |
(d) (i) Describe, in words, the rule for continuing the sequence for the number of dots.
(ii) The expression for the number of dots in Diagram n is \(n^2 + n – 2\).
Find the number of dots in Diagram 12.
(e) (i) Write down an expression for the number of crosses in Diagram n.
(ii) Diagram n has 100 crosses.
Find the value of n.
n = …………………………………………
Answer/Explanation
Answer:
(a) 2
(b) 3 dots correctly placed
4 crosses correctly placed
(c) 18 28
10 12
(d) (i) Add two more each time oe
(ii) 154
(e)(i) 2n + 2 oe final answer
(ii) 49
Question
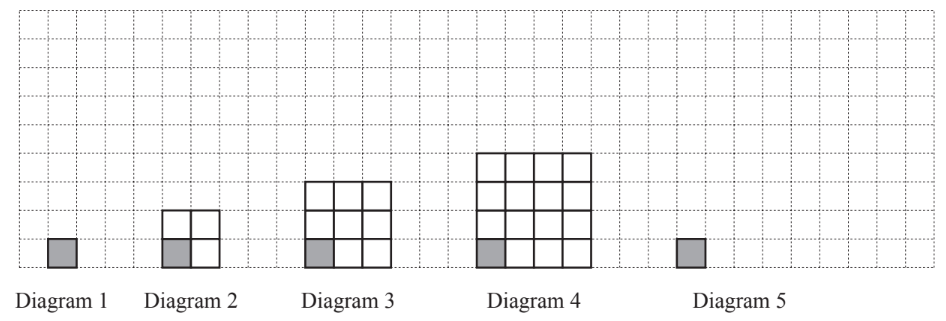
Each of the diagrams above shows one small shaded square and a number of small unshaded squares.
The diagrams form a sequence.
(a) Complete Diagram 5.
(b) Complete the table.
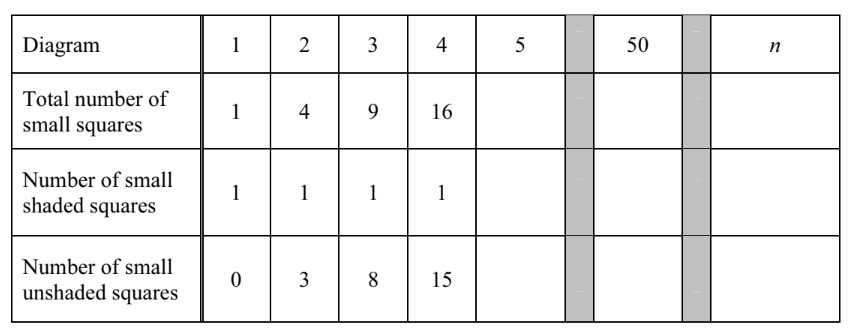
(c) Diagram p has 9999 small unshaded squares. Find p.
▶️Answer/Explanation
(a) 5 by 5 shape
(b) First row $25 \quad 2500 \quad n^2$ Second row $\quad 1 \quad 1 \quad 1$ Third row $24 \quad 2499 \quad n^2-1$
(c) 100
Question
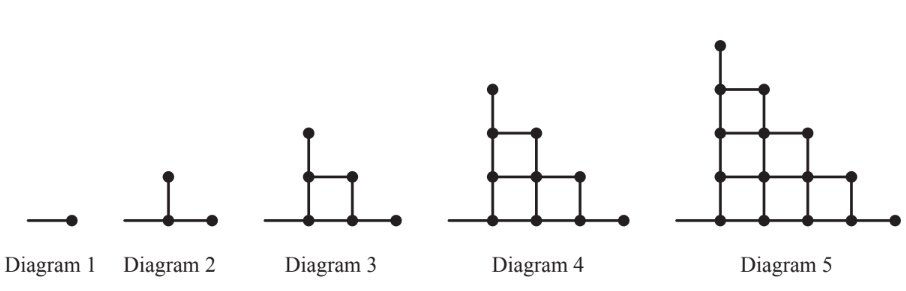
The diagrams show a pattern of lines and dots.
(a) Complete the table below.
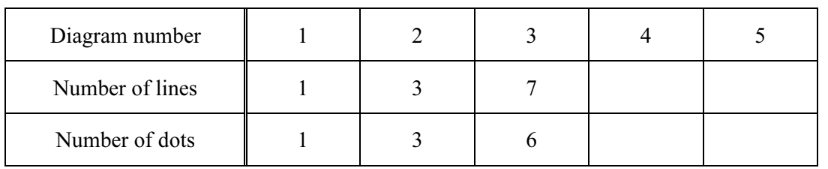
(b) Work out the number of lines and the number of dots in Diagram 7.
(c) The number of dots in Diagram $n$ is $\frac{1}{2} n(n+1)$.
(i) Use this formula to check your result for Diagram 5 . You must show your working.
(ii) How many dots are there in Diagram 20?
(d) The number of lines in Diagram $n$ is $n^2+k n+1$.
Use the information about Diagram 3 from the table to calculate the value of $k$.
▶️Answer/Explanation
(a) $13 \quad 21$
$10 \quad 15$
(b) 43 28
(c) (i) $1 / 2 \times 5 \times 6$ $=15$ seen
(ii) $1 / 2 \times 20 \times 21$ $=210$
(d) $\quad(\mathrm{k}=)-1$
