Question
Paulo and Jim each buy sacks of rice but from different shops.
Paulo pays \($72 \)for sacks costing \($m\) each.
Jim pays \($72 \)for sacks costing \($(m + 0.9) \)each.
(a) (i) Find an expression, in terms of m, for the number of sacks Paulo buys.
…………………………………………
(ii) Find an expression, in terms of m, for the number of sacks Jim buys.
…………………………………………
(b) Paulo buys 4 more sacks than Jim.
Write down an equation, in terms of m, and show that it simplifies to \(10m^{2}+9m-162=0.\)
(c) (i) Solve\( 10m^{2}+9m-162=0.\)
m = ……………….. or m = ………………..
(ii) Find the number of sacks of rice that Paulo buys.
…………………………………………
Answer/Explanation
(a)(i)\(\frac{72}{m}\)
(ii)\(\frac{72}{m+0.9}\)
(b)\(\frac{72}{m}-\frac{72}{m+0.9}=4\)
72(m+0.9)-72m=4m(m+0.9)
[72m-72m]+64.8=4m^{2}+3.6m
Correct explanation to\( 10m^{2}+9m-162=0\)
(c)(i)3.6 and -4.5 final answer
(ii) 20
Question
(a) Solve the following equations.
(i) $\frac{5}{w}=\frac{3}{w+1}$
(ii) $(y+1)^2=4$
(iii) $\frac{x+1}{3}-\frac{x-2}{5}=2$
(b) (i) Factorise $u^2-9 u-10$.
(ii) Solve the equation $u^2-9 u-10=0$.
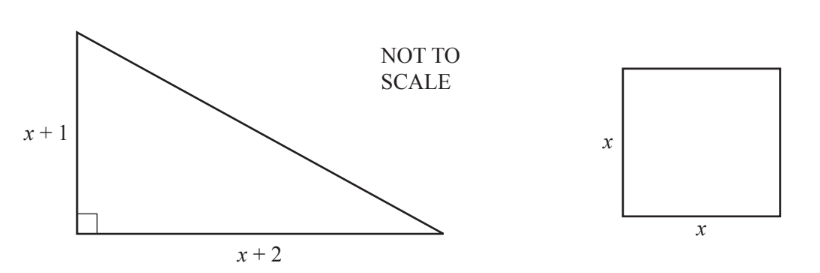
The area of the triangle is equal to the area of the square. All lengths are in centimetres.
(i) Show that $x^2-3 x-2=0$.
(ii) Solve the equation $x^2-3 x-2=0$, giving your answers correct to 2 decimal places. Show all your working.
(iii) Calculate the area of one of the shapes.
▶️Answer/Explanation
(a) (i) -2.5 oe
(ii) -3 or 1
(iii) 9.5 oe
(b) (i) $(u-10)(u+1)$
(ii) $-1,10$
(c) (i) $\frac{(x+1)(x+2)}{2}=x^2 \quad$ oe
$
\begin{aligned}
& ((x+1)(x+2)=) x^2+x+2 x+2 \\
& x^2+x+2 x+2=2 x^2 \\
& x^2-3 x-2=0
\end{aligned}
$
(ii) $\frac{-(-3) \pm \sqrt{(-3)^2-4(1)(-2)}}{2(1)}$
–0.56, 3.56
(iii) 12.7 or 12.67 to 12.69 ft