Question
The diagram shows the speed-time graph of a bus journey between two bus stops.
Hamid runs at a constant speed of 4m/s along the bus route.
He passes the bus as it leaves the first bus stop.
The bus arrives at the second bus stop after 60 seconds.
How many metres from the bus is Hamid at this time?
Answer/Explanation
Ans: 180 www
Question
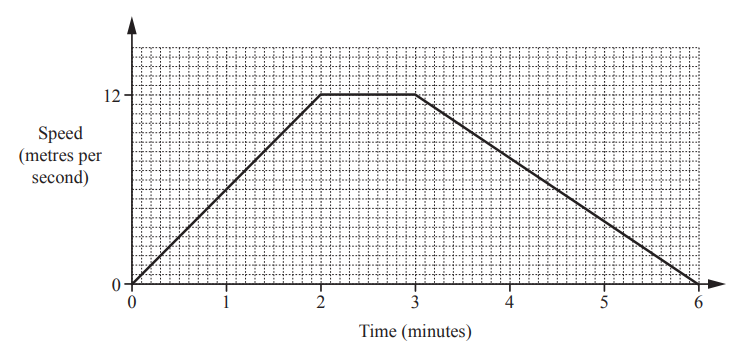
A tram leaves a station and accelerates for 2 minutes until it reaches a speed of 12 metres per second.
It continues at this speed for 1 minute.
It then decelerates for 3 minutes until it stops at the next station.
The diagram shows the speed-time graph for this journey.
Calculate the distance, in metres, between the two stations.
Answer/Explanation
Ans: 2520 m
Question
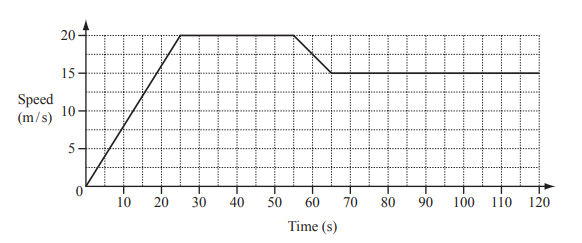
The diagram shows the speed-time graph for the first 120 seconds of a car journey.
(a) Calculate the acceleration of the car during the first 25 seconds.
Answer/Explanation
Ans: 0.8
(b) Calculate the distance travelled by the car in the first 120 seconds.
Answer/Explanation
Ans: 1850
Question
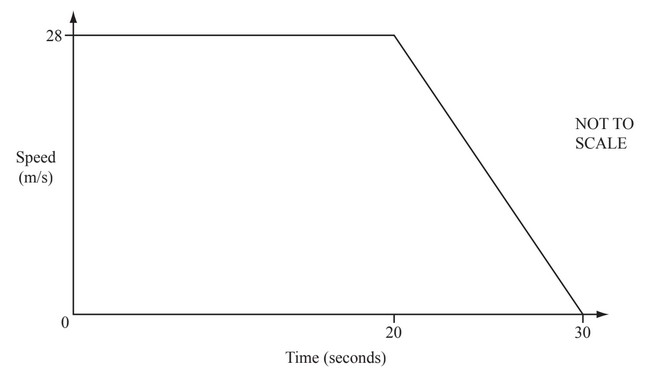
The diagram shows the speed-time graph of a car.
It travels at 28m/s for 20 seconds and then decelerates until it stops after a further 10 seconds.
(a) Calculate the deceleration of the car.
(b) Calculate the distance travelled during the 30 seconds.
Answer/Explanation
Ans:
(a) 2.8 oe \(m/s^2\)
(b) 700 m
Question
A car travels at 56km/h.
Find the time it takes to travel 300 metres.
Give your answer in seconds correct to the nearest second.
Answer/Explanation
Ans: 19 nfww
Question
A train travels for m minutes at a speed of x metres per second.
(a) Find the distance travelled, in kilometres, in terms of m and x.
Give your answer in its simplest form.
………………………………….. km
(b) When m = 5, the train travels 10.5km.
Find the value of x.
x = …………………………………………
Answer/Explanation
Ans:
(a) \(\frac{3mx}{50}\) or 0.06 mx
(b) 35
Question
The diagram shows information about the first 100 seconds of a car journey.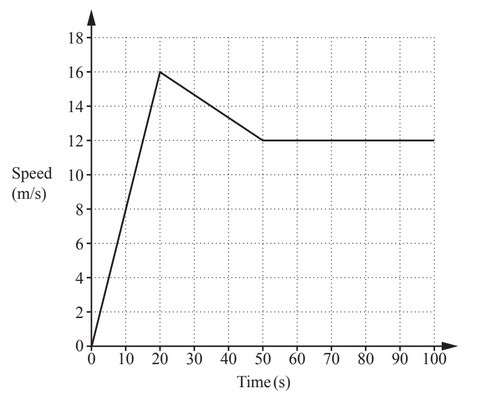
(a) Calculate the acceleration during the first 20 seconds of the journey.
……………………………….. \(m/s^2\)
(b) Work out the total distance travelled by the car in the 100 seconds.
………………………….. m
Answer/Explanation
Ans:
0.8 or \(\frac{4}{5}\)
Question
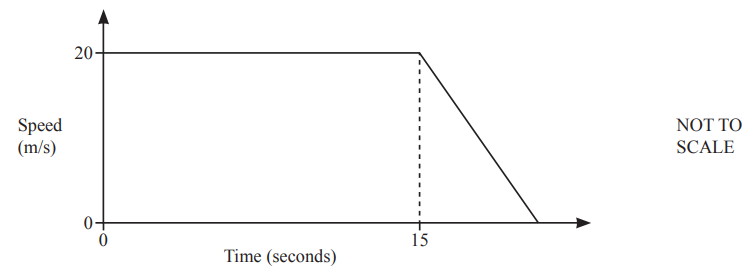
A car travels at 20m/s for 15 seconds before it comes to rest by decelerating at 2.5m/s2.
Find the total distance travelled.
m [5]
Answer/Explanation
Ans:
26 380
Question
The speed-time graph shows the first 60 seconds of a train journey.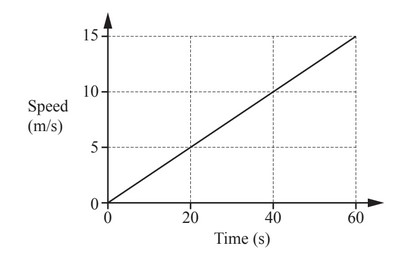
(a) Find the acceleration of the train.
……………………………………m/\(s^2\)
(b) Calculate the distance the train has travelled in this time.
Give your answer in kilometres.
…………………………………….. km
Answer/Explanation
Ans:
(a) 0.25 or \(\frac{1}{4}\)
(b) 0.45
Question
Petra begins a journey in her car.
She accelerates from rest at a constant rate of 0.4 m/\(s^2\) for 30 seconds.
She then travels at a constant speed for 40 seconds.
On the grid, draw the speed-time graph for the first 70 seconds of Petra’s journey.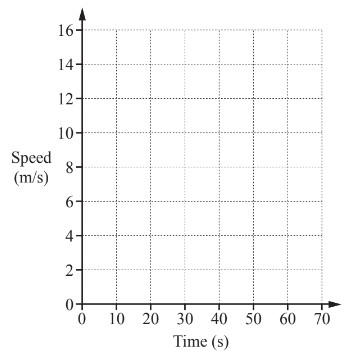
Answer/Explanation
Ans:
Diagonal line from
(0, 0) to (30, 12)
and
Horizontal line from
(30, 12) to (70, 12)
Question
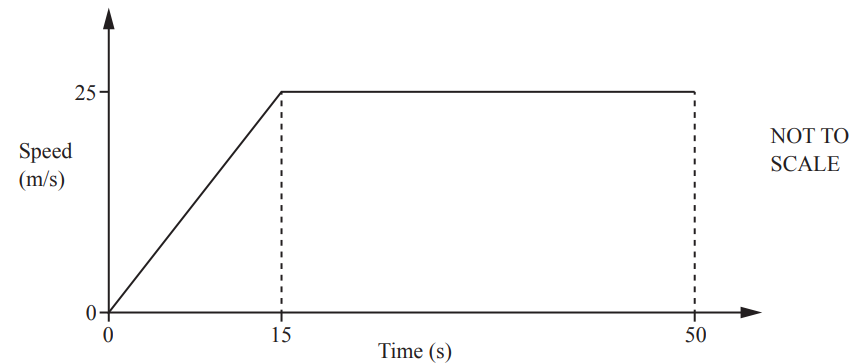
The speed–time graph shows the first 50 seconds of a journey.
Calculate
(a) the acceleration during the first 15 seconds,
__ m/s2 [1]
(b) the distance travelled in the 50 seconds.
__ m [3]
Answer/Explanation
Ans:
22(a) \(1\frac{2}{3}\) or 1.67 or 1.666 to 1.667
22(b) 1062.5
Question
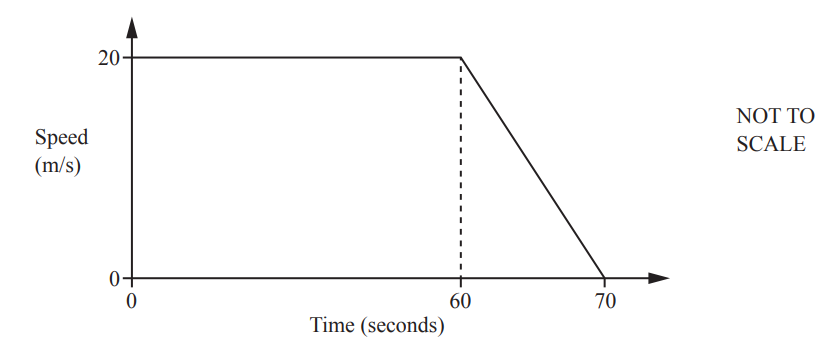
The diagram shows information about the final 70 seconds of a car journey.
(a) Find the deceleration of the car between 60 and 70 seconds.
m/s2 [1]
(b) Find the distance travelled by the car during the 70 seconds.
m [3]
Answer/Explanation
Ans:
24(a) 2
24(b) 1300
Question
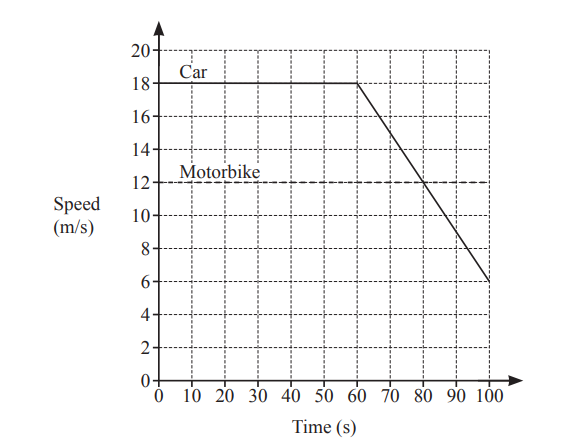
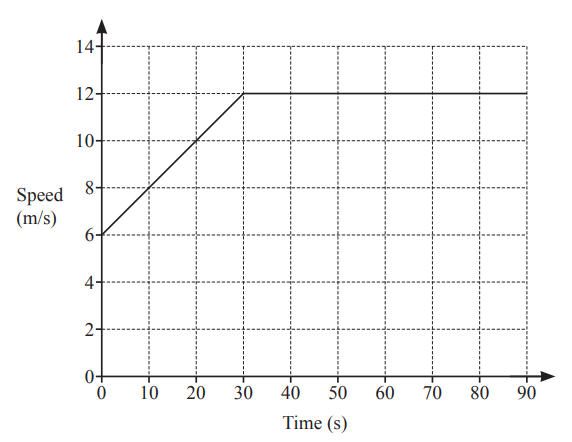
The diagram shows the speed–time graph for 100 seconds of the journey of a car and of a motorbike.
(a) Find the deceleration of the car between 60 and 100 seconds.
………………………………….. \(m/s^{2}\)
(b) Calculate how much further the car travelled than the motorbike during the 100 seconds.
……………………………………… m
Answer/Explanation
(a) 0.3
(b) 360
Question
The diagram shows the speed–time graph for 90 seconds of a journey.
Calculate the total distance travelled during the 90 seconds.
……………………………………… m
Answer/Explanation
990
Question
A hummingbird beats its wings 24 times per second.
(a) Calculate the number of times the hummingbird beats its wings in one hour.
(b) Write your answer to part(a) in standard form
Answer/Explanation
(a)Using unitary method ,
1 sec = 24 times
60\(\times\) 60 sec = 24\(\times\)3600
= 86400 times
(b) Standard form basically means writing the numbers in the power of 10
So, 86400 in standard form is : 8.64\(\times 10^4\)
Question
A train leaves Barcelona at 21:28 and takes 10 hours and 33 minutes to reach Paris.
(a) Calculate the time the next day when the train arrives in Paris.
(b) The distance from Barcelona to Paris is 827 km.
Calculate the average speed of the train in kilometres per hour.
Answer/Explanation
(a) 21:28 is 9:28 pm in 12 hours format clock
So, Adding 10 hours 33 minutes to 9:28 pm gives 8:01 am
So, the train will be reaching by 8:01 ,the next day
(b) Average speed=\(\frac{ Total distance}{Total time}/)
Now , 10 hours 33 minutes= 10+33/60 minutes=10.5 hours
So, putting it into formula :
Average speed= \(\frac{ 827km}{10.5hours}/)
=78.38 km/hour
Question
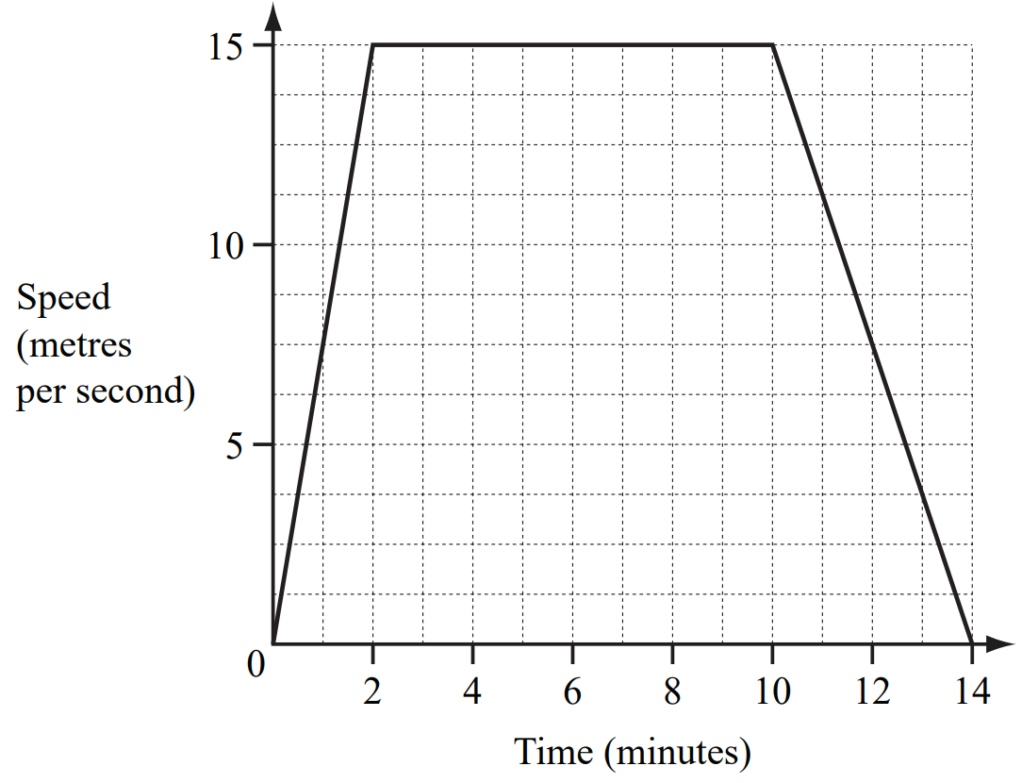
The diagram shows the speed-time graph of a train journey between two stations.
The train accelerates for two minutes, travels at a constant maximum speed, then slows to a stop.
(a) Write down the number of seconds that the train travels at its constant maximum speed.
(b) Calculate the distance between the two stations in metres.
(c) Find the acceleration of the train in the first two minutes.
Give your answer in m/s2
Answer/Explanation
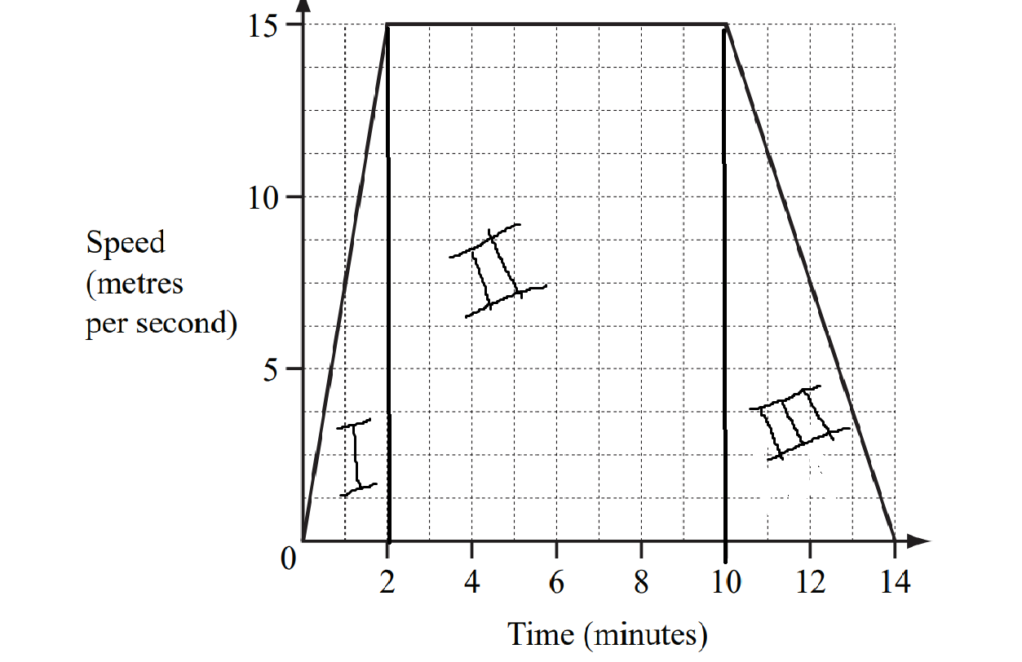
Distance is I= ut+\(\frac{1}{2}a t^2\)
=0(120)+\(\frac{1}{2}\times\frac{5}{8}\times 120\times 120
900 m
Distance is II= 15m/s\(\times (8\times 60\)
15\(\times 480\)
=7200 m
Similarly , Distance is III=180-450
= 1350 m
Total distance =900+72300+1350m
= 9450 m
(c) a=\(\frac{\Delta V}{\Delta V}\)
a=\(\frac{V_f-V_i}{T_f-T_i}\)
a=\(\frac{15-0}{(2.60)-0}\)
=\(\frac{1}{8}\) m/\(s^2)\)
Question
A container ship travelled at 14 km/h for 8 hours and then slowed down to 9 km/h over a period of
30 minutes.
It travelled at this speed for another 4 hours and then slowed to a stop over 30 minutes.
The speed-time graph shows this voyage.
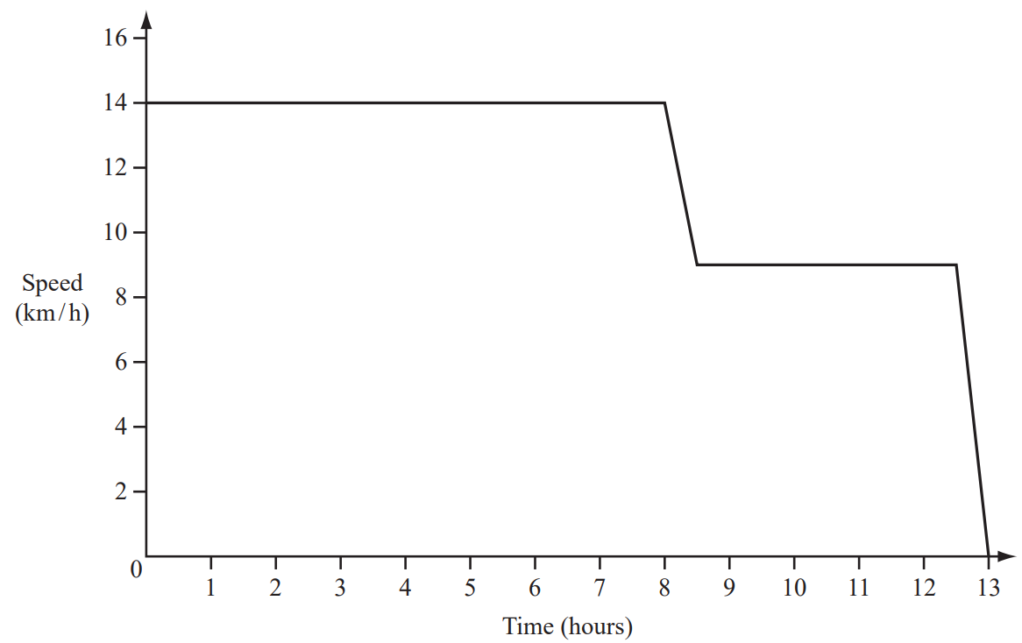
(a) Calculate the total distance travelled by the ship.
(b) Calculate the average speed of the ship for the whole voyage.
Answer/Explanation
(a) Distance = speed \(\times time\)
= 156
(b) 12
Question
A person in a car, travelling at 108 kilometres per hour, takes 1 second to go past a building on the side of the road. Calculate the length of the building in metres.
▶️Answer/Explanation
To calculate the length of the building. We can use the formula,
Distance \(= Speed \times Time\)
Given that the speed of the car is 108 kilometers per hour and the time taken to go past the building is 1 second, we need to convert the speed from kilometers per hour to meters per second.
1 kilometer = 1000 meters
1 hour = 3600 seconds
Converting the speed,
108 kilometers per hour\(=\frac{108\times 1000 m}{3600 s}=30ms^{-1}\)
Now, we can calculate the distance covered by the car in 1 second:
\(Distance = Speed\times Time = 30 ms^{-1}\times 1s =\) 30 meters
Therefore, the length of the building is 30 meters.
Question
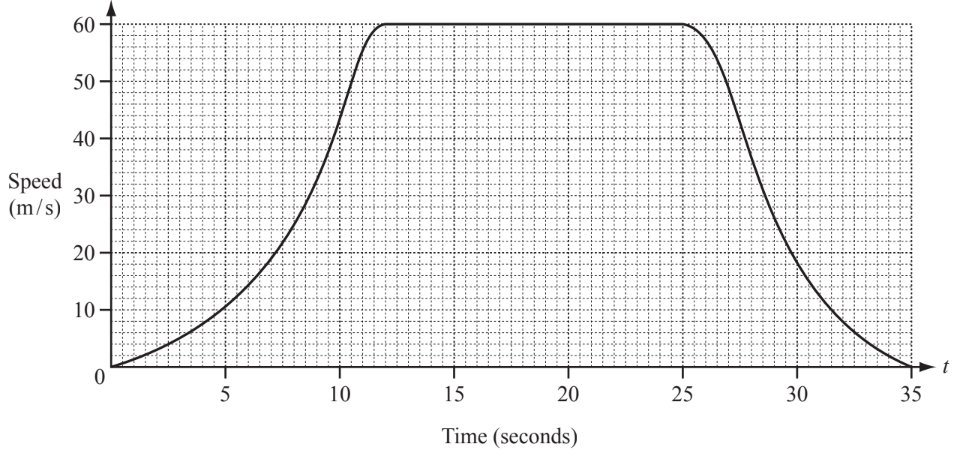
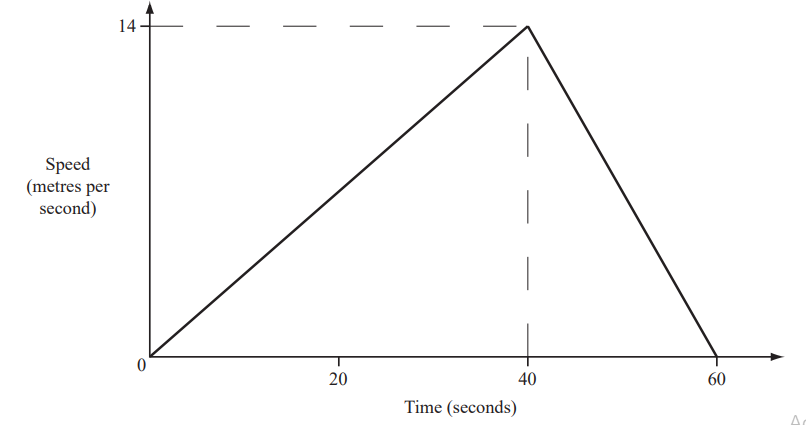
The graph shows the speed of a sports car after $t$ seconds.
It starts from rest and accelerates to its maximum speed in 12 seconds.(a) (i) Draw a tangent to the graph at $t=7$.
(ii) Find the acceleration of the car at $t=7$.
(b) The car travels at its maximum speed for 13 seconds.
Find the distance travelled by the car at its maximum speed.
▶️Answer/Explanation
(a) (i) Tangent
(ii) 4.4 to 6
(b) 780
Question
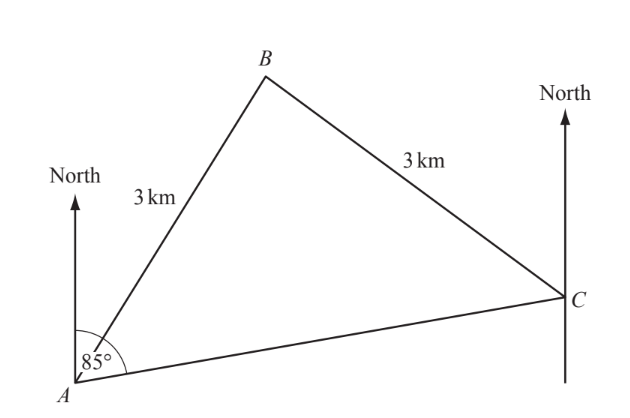
A, B and C are three places in a desert. Tom leaves A at 06 40 and takes 30 minutes to walk directly to B, a distance of 3 kilometres. He then takes an hour to walk directly from B to C, also a distance of 3 kilometres.
(a) At what time did Tom arrive at C?
(b) Calculate his average speed for the whole journey.
(c) The bearing of C from A is 085°. Find the bearing of A from C.
▶️Answer/Explanation
(a) (0)810 or 8:10 etc.
(b) 4
(c) 265
Question
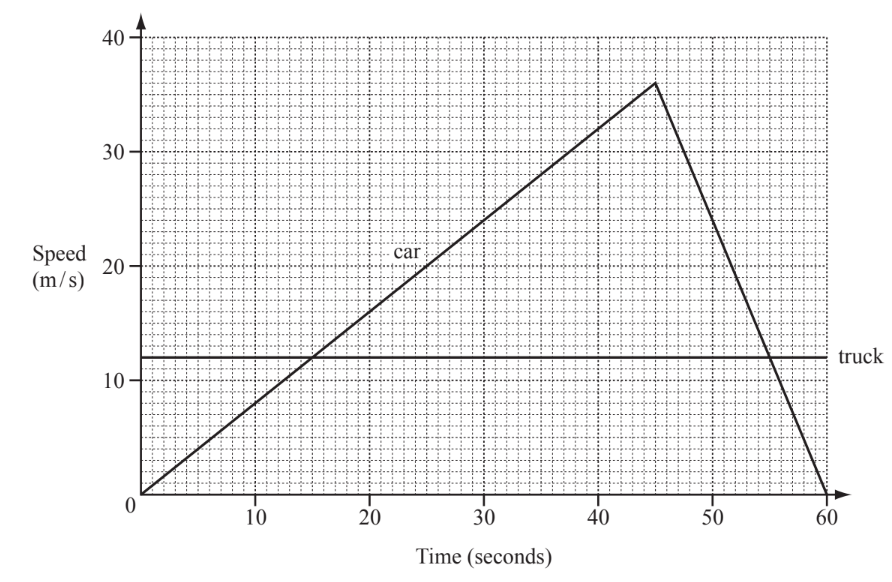
The graph shows the speed of a truck and a car over 60 seconds.
(a) Calculate the acceleration of the car over the first 45 seconds.
(b) Calculate the distance travelled by the car while it was travelling faster than the truck.
▶️Answer/Explanation
(a) 0.8 or 4/5 cao
(b) 960 www