Question
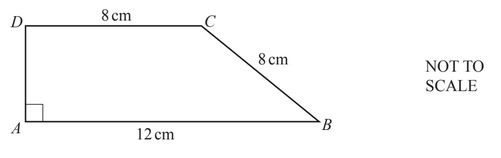
Calculate the area of this trapezium.
……………………………………. \(cm^2\)
Answer/Explanation
Ans:
69.3 or 69.28…
Question
The thickness of one sheet of paper is \(8 \times 10^{-3}\) cm.
Work out the thickness of 250 sheets of paper.
………………….. cm
Answer/Explanation
Ans:
2
Question
Find the area of a regular hexagon with side length 7.4cm.
Answer/Explanation
142 or 142.2 to 142.3
Question
Rectangle A measures 3cm by 8 cm.
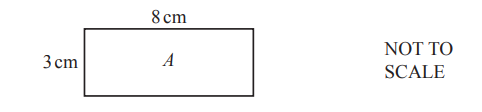
Five rectangles congruent to A are joined to make a shape.
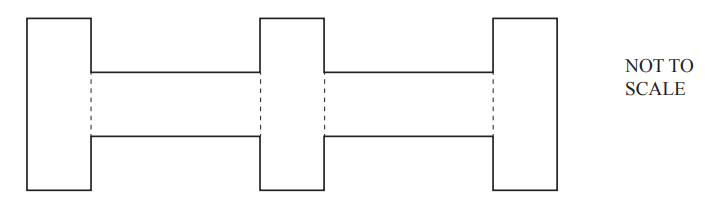
Work out the perimeter of this shape.
……………………………………. cm
Answer/Explanation
86
Question
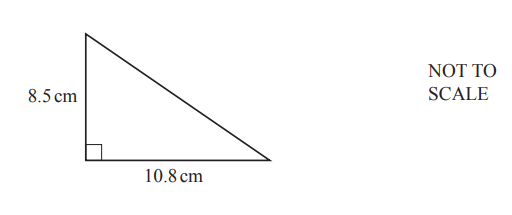
The diagram shows a right-angled triangle.
(a) Calculate the area.
……………………………………\( cm^{2}\)
(b) Calculate the perimeter.
…………………………………….. cm.
Answer/Explanation
(a)45.9
(b)33.0 or 33.04
Question
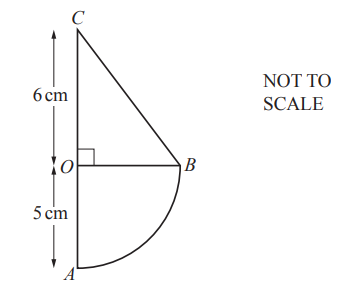
The diagram shows a shape made from a quarter-circle, OAB, and a right-angled triangle OBC.
The radius of the circle is 5cm and OC = 6cm.
Calculate the area of the shape.
…………………………………… \(cm^{2}\)
Answer/Explanation
34.6 or 34.63 to 34.64
Question
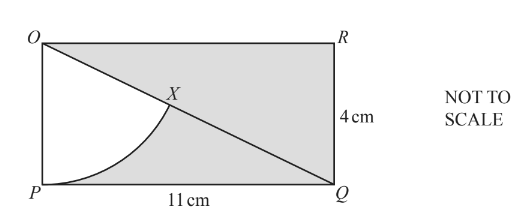
The diagram shows a rectangle OPQR with length 11cm and width 4cm.
OQ is a diagonal and OPX is a sector of a circle, centre O.
Calculate the percentage of the rectangle that is shaded.
Answer/Explanation
77.8 or 77.77 to 77.80