Question
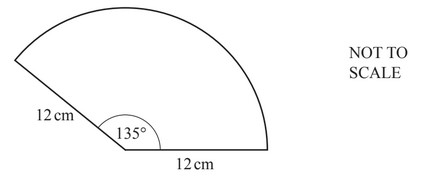
The diagram shows a sector of a circle of radius 12cm with an angle of 135°.
Calculate the perimeter of the sector.
Answer/Explanation
Ans:
52.3 or 52.27 to 52.28 cm
Question
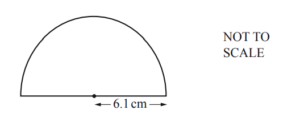
A protractor is a semi-circle of radius 6.1cm.
Calculate the perimeter of the protractor.
Answer/Explanation
Ans: 31.4 or 31.36 to 31.37
Question
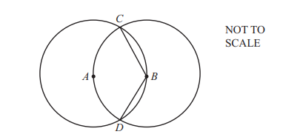
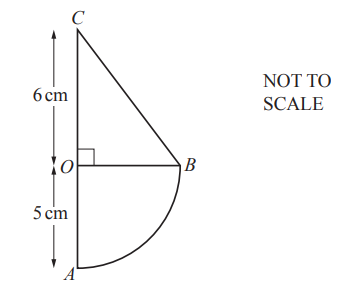
Two circles, centres A and B, are each of radius 8cm and intersect at C and D.
Each circle passes through the centre of the other circle.
(a) Explain why angle CBD is 120°.
Answer/Explanation
Ans: CBA and BDA are equilateral oe
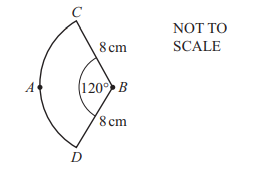
(b) For the circle, centre B, fi nd the area of the sector BCD.
Answer/Explanation
Ans: 67[.0] or 67.02 to 67.03
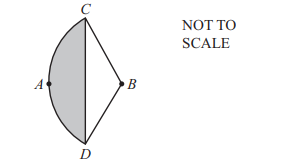
(c) (i) Find the area of the shaded segment CAD.
Answer/Explanation
Ans: 39.3 or 39.28 to 39.33
(ii) Find the area of overlap of the two circles.
Answer/Explanation
Ans: 78.6 or 78.7 or 78.56 to 78.66
Question
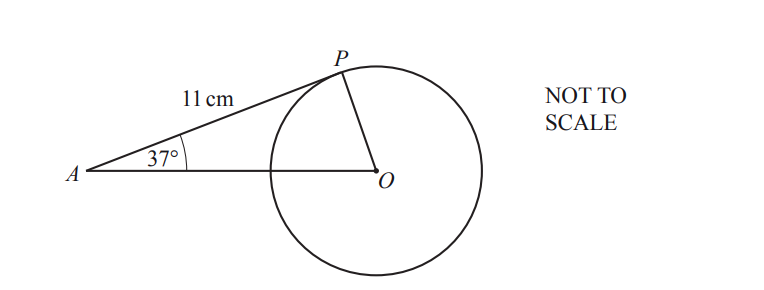
In the diagram, AP is a tangent to the circle at P.
O is the centre of the circle, angle PAO = 37° and AP = 11cm.
(a) Write down the size of angle OPA.
Answer/Explanation
Ans: 90
(b) Work out the radius of the circle.
Answer/Explanation
Ans: 8.29 or 8.289… to 8.29
Question
AB is an arc of a circle, centre O, radius 9cm.
The length of the arc AB is 6 rcm.
The area of the sector AOB is \(krcm^2\).
Find the value of k.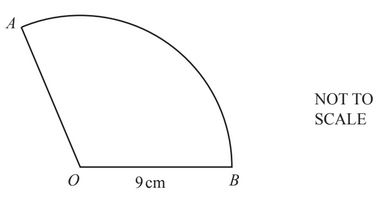
k = ……………………….
Answer/Explanation
Ans:
27
Question
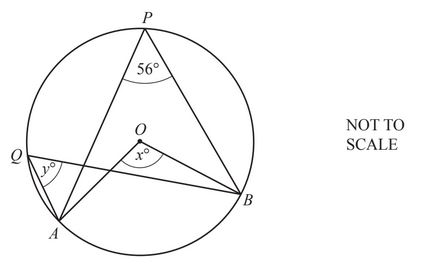
A, B, P and Q lie on the circle, centre O.
Angle APB = 56°.
Find the value of
(a) x,
x = …………………………
(b) y.
y = …………………………………………..
Answer/Explanation
Ans:
(a) 112
(b) 56
Question
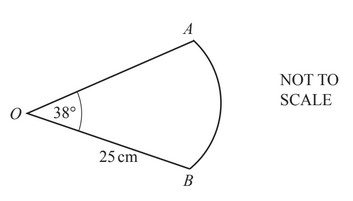
The diagram shows a sector of a circle, centre O, radius 25 cm.
The sector angle is 38°.
Calculate the length of the arc AB.
Give your answer correct to 4 significant figures.
AB = …………. cm
Answer/Explanation
Ans:
16.58 cao
Question
ABCD is a rhombus with side length 10cm.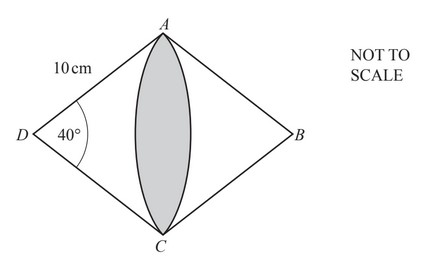
Angle ADC = 40°.
DAC is a sector of a circle with centre D.
BAC is a sector of a circle with centre B.
Calculate the shaded area.
Answer/Explanation
Ans:
5.53 or 5.54 or 5.534 to 5.543…
Question
(a) 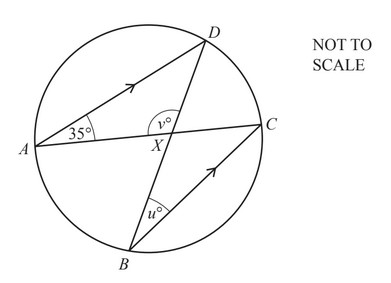
A, B, C and D are points on the circle.
AD is parallel to BC.
The chords AC and BD intersect at X.
Find the value of u and the value of v.
u = ……………………….
v = ………………….
(b) 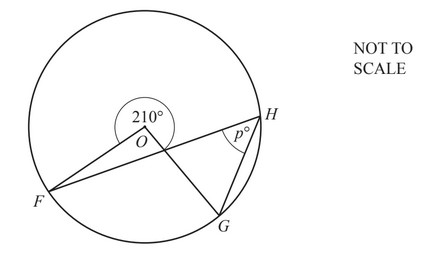
F, G and H are points on the circle, centre O.
Find the value of p.
p = ………………
Answer/Explanation
Ans:
(a) [u =] 35
[v =]110
(b) 75
Question
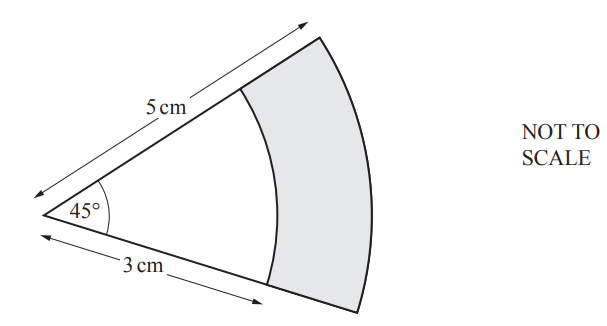
The diagram shows two sectors of circles with the same center.
Calculate the shaded area.
cm2 [3]
Answer/Explanation
Ans:
17 6.28 or 6.283 to 6.284
Question
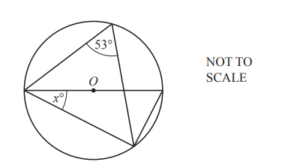
The diagram shows a circle, centre O.
Find the value of x.
Answer/Explanation
Ans: 37
Question
Calculate the area of a circle with radius 5.1cm.
\(…………………………………cm^{2}\)
Answer/Explanation
81.7 or 81.71 to 81.72…
Question
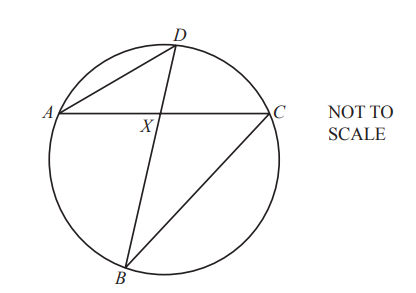
A, B, C and D are points on the circumference of the circle.
AC and BD intersect at X.
(a) Complete the statement.
Triangle ADX is …………………………………………….. to triangle BCX.
(b) The area of triangle ADX is 36cm^{2} and the area of triangle BCX is 65.61cm^{2}.
AX = 8.6 cm and DX = 7.2cm.
Find BX
Answer/Explanation
(a)similar
(b)11.61
Question
The number of people swimming in a pool is recorded each day for 12 days.
24 28 13 38 15 26
45 21 48 36 18 38
(a) Complete the stem-and-leaf diagram.

(b) Find the median number of swimmers.
………………………………………….
Answer/Explanation
(a)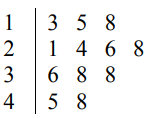
(b)27
Question
The diagram shows a shape made from a quarter-circle, OAB, and a right-angled triangle OBC.
The radius of the circle is 5cm and OC = 6cm.
Calculate the area of the shape.
…………………………………… \(cm^{2}\)
Answer/Explanation
34.6 or 34.63 to 34.64
Question
Calculate the circumference of a circle with radius 4.7cm.
Answer/Explanation
29.5 or 29.53…
Question
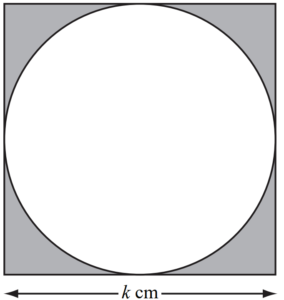
The diagram shows a square of side k cm.
The circle inside the square touches all four sides of the square.
(a) The shaded area is A\((cm)^2\)
Show that 4A=4\(k^2\)-\pi\((k)^2\)
(b) Make k the subject of the formula 4A=4\(k^2\)-\pi\((k)^2\)
Answer/Explanation
Area of square= \(K\times K =K^2(cm)^2\)
Given, Shaded region= \(A (cm)^2\)
Area of circle=\(\pi(\frac{K}{4})^2
A=\(K^2\)-\(\pi(\frac{(K)^2}{4})
4A=4\(K^2-\pi K^2\) Hence Proved
Question
A circle has a radius of 50 cm.
(a) Calculate the area of the circle in \({cm}^2\)
(b) Write your answer to part (a) in \({m}^2\)
Answer/Explanation
Area of the circle= \(\pi r^2\)
where, r is radius of circle
=\(\pi.50.50\)
=\(\pi 2500 {cm}^2\)
=2500.3.14
=25.314
=7850 \({cm}^2\)
Question
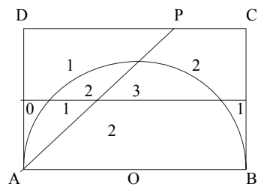
ABCD is a rectangle with AB = 10 cm and BC = 6 cm. MN is the perpendicular bisector of BC. AP is the bisector of angle BAD. O is the midpoint of AB and also the centre of the semicircle, radius 5 cm.
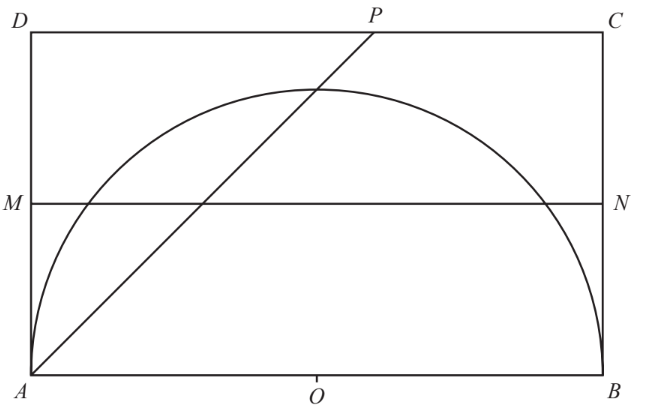
Write the letter R in the region which satisfies all three of the following conditions.
• nearer to AB than to AD
• nearer to C than to B
• less than 5 cm from O
▶️Answer/Explanation