Question
\(M = \begin{pmatrix}5 &-4 \\2 &3 \end{pmatrix}\)
Find
(a) M2,
Answer/Explanation
Ans: \(\begin{pmatrix}17 &-32 \\16 &1 \end{pmatrix}\)
(b) 2M,
Answer/Explanation
Ans: \(\begin{pmatrix}10 &-8 \\4 &6 \end{pmatrix}\)
(c) |M| , the determinant of M,
Answer/Explanation
Ans: 23 cao
(d) M-1.
Answer/Explanation
Ans: \(\frac{1}{23}\begin{pmatrix}3 &4 \\-2 &5 \end{pmatrix}\)
Question
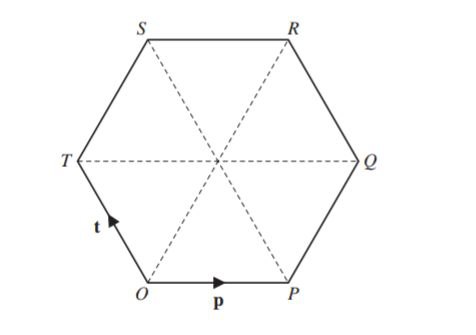
O is the origin and OPQRST is a regular hexagon.
\(\overrightarrow{OP}=p and \overrightarrow{OT}=t.\)
Find, in terms of p and t, in their simplest forms,
(a) \(\overrightarrow{PT}\),
Answer/Explanation
Ans: -p+t
(b) \(\overrightarrow{PR}\),
Answer/Explanation
Ans: p+2t
(c) the position vector of R.
Answer/Explanation
Ans: 2(p + t) or 2p + 2t
Question
(a) Work out \(\begin{pmatrix}1 &-2 \\3 &4 \end{pmatrix}\begin{pmatrix}-5 &-3 \\2 &1 \end{pmatrix}.\)
Answer/Explanation
Ans: \(\begin{pmatrix}-9 &-5 \\-7 &-5 \end{pmatrix}\)
(b) Find the inverse of \(\begin{pmatrix}1 &-2 \\3 &4 \end{pmatrix}\).
Answer/Explanation
Ans: \(\frac{1}{10}\begin{pmatrix}4 &2 \\-3 &1 \end{pmatrix} oe\)
(c) Explain why it is not possible to work out \(\begin{pmatrix}1 &-2 \\3 &4 \end{pmatrix}+\binom{3}{2}.\)
Answer/Explanation
Ans: Not the same order oe
Question
\(M = \begin{pmatrix}5 &2 \\-3 &4 \end{pmatrix}\) \(N = \begin{pmatrix}-1 &-2 \\2 &6 \end{pmatrix}\)
Calculate
(a) MN,
Answer/Explanation
Ans: \(\begin{pmatrix}-1 &2 \\11 &30 \end{pmatrix}\)
(b) M−1, the inverse of M.
Answer/Explanation
Ans: \(\frac{1}{26}\begin{pmatrix}4 &-2 \\3 &5 \end{pmatrix}oe\)
Question
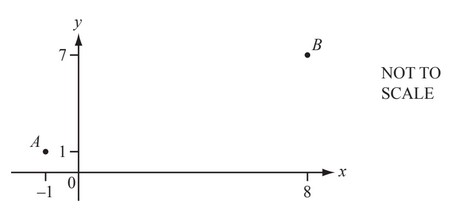
A is the point (–1, 1) and B is the point (8, 7).
(a) Write \(\overrightarrow{AB}\) as a column vector.
(b) Find \(|\overrightarrow{AB}|\).
(c) \(\overrightarrow{AC} = 2 \overrightarrow{AB}\).
Write down the co-ordinates of C.
Answer/Explanation
Ans:
(a) \(\binom{9}{6}\)
(b) 10.8 or 10.81 to 10.82
(c) (17, 13)
Question
\(A = \begin{pmatrix}
1 & 2\\
3 & 4
\end{pmatrix}\) \(B =\begin{pmatrix}
4 & 3\\
1 & 2
\end{pmatrix}\)
Find
(a) AB
(b) \(B^{-1}\), the inverse of B,
Answer/Explanation
Ans:
(a) AB = \(\begin{pmatrix}
6 & 7\\
16 & 17
\end{pmatrix}\)
(b) \(B^{-1}\) = \(\frac{1}{5} \begin{pmatrix}
2 & -3\\
-1 & 4
\end{pmatrix}\)
Question
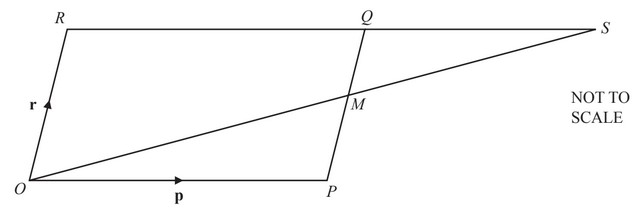
OPQR is a parallelogram, with O the origin.
M is the midpoint of PQ.
OM and RQ are extended to meet at S.
\(\overrightarrow{OP}=p\) and \(\overrightarrow{OR}=r\).
(a) Find, in terms of p and r, in its simplest form,
(i) \(\overrightarrow{OM}\),
(ii) the position vector of S.
(b) When \(\overrightarrow{PT} = -\frac{1}{2}p + r\), what can you write down about the position of T?
Answer/Explanation
Ans:
(a) (i) \(\overrightarrow{OM} = p + \frac{1}{2} r\)
(ii) 2p + r
(b) Midpoint of RQ
Question
y varies directly with \(\sqrt{x+5}.\)
y = 4 when x = –1.
Find y when x = 11.
Answer/Explanation
Ans:
Question
(a) Calculate \(\begin{pmatrix}3 &7 \\-1 &4 \end{pmatrix}\begin{pmatrix}-2 &1 \\4 &2 \end{pmatrix}.\)
Answer/Explanation
Ans: \(\begin{pmatrix}22 &17 \\18 &7 \end{pmatrix}\)
(b) Calculate the inverse of \(\begin{pmatrix}5 &3 \\6&4\end{pmatrix}.\)
Answer/Explanation
Ans: \(\frac{1}{2}\begin{pmatrix}4 &-3 \\-6 &5 \end{pmatrix}\)
Question
Work out.
(a) \(2\binom{3}{5}-\binom{1}{2}\)
(b) (1 2)\(\binom{2}{3}\)
Answer/Explanation
Ans:
(a) \(\binom{5}{8}\)
(b) (8) final answer
Question
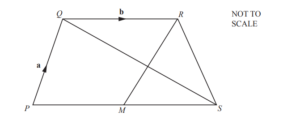
PQRS is a quadrilateral and M is the midpoint of PS.
\(\overrightarrow{PQ}=a, \overrightarrow{QR}=b and \overrightarrow{SQ}=a-2b.\)
(a) Show that \(\overrightarrow{PS}=2b.\)
Answer/Explanation
Ans: a + 2b − a or a − ( a − 2b) oe
(b) Write down the mathematical name for the quadrilateral PQRM, giving reasons for your answer.
Answer/Explanation
Ans: Parallelogram
PM equal and parallel to QR
or
PM or PS parallel to QR
and MR found = a so 2 pairs of
parallel sides
Question
\(M=\begin{pmatrix}
5 &3 \\
3&-2
\end{pmatrix}\) \(N = \begin{pmatrix}
3 & -6 \\
4& 2
\end{pmatrix}\)
Calulate
(a) MN,
(b) \(M^{-1}\).
Answer/Explanation
Ans:
(a) \(\begin{pmatrix}
27 & -24\\
-5 & -10
\end{pmatrix}\)
(b) \(-\frac{1}{13}\begin{pmatrix}
-2 & -3\\
-1 & 5
\end{pmatrix}\) oe isw
Question
Find the inverse of the matrix \(\begin{pmatrix}
3 & -2\\
-8 & 7
\end{pmatrix}\)
Answer/Explanation
Ans:
\(\frac{1}{5} \begin{pmatrix}
7 & 2\\
8 & 3
\end{pmatrix}\) oe isw
Question
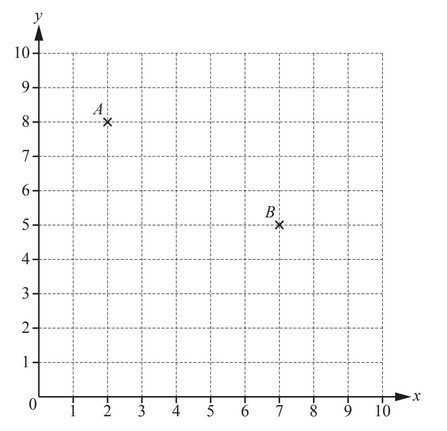
Points A and B are marked on the grid.
\(\overheadarrow{BC}\) = \(\begin{pmatrix}
-4\\0
\end{pmatrix}\)
(a) On the grid, plot the point C.
(b) Write \(\overheadarrow{AC}\) as a column vector.
(c) \(\overheadarrow{DE}\) is a vector that is perpendicular to \(\overheadarrow{BC}\).
The magnitude of \(\overheadarrow{DE}\) is equal to the magnitude of \(\overheadarrow{BC}\).
Write down a possible column vector for \(\overheadarrow{DE}\).
Answer/Explanation
Ans:
(a) Point at (3, 5)
(b) \(\begin{pmatrix}
1\\-3
\end{pmatrix}\)
(c) \(\begin{pmatrix}
0\\4
\end{pmatrix}
or
\begin{pmatrix}
0\\-4
\end{pmatrix}\)
FT their \(\overheadarrow{AC}\)
Question
(a) D is the point (2, ‒5) and \(\overheadarrow{DE} =\begin{pmatrix}
7\\1
\end{pmatrix}\)
Find the co-ordinates of the point E.
(………………… , …………………)
(b) v= \(\begin{pmatrix}
t\\ 12
\end{pmatrix}\) and |v| = 13.
Work out the value of t, where t is negative.
t = …………………………………………..
Answer/Explanation
Ans:
(a) (9, −4)
(b) -5
Question
The diagram shows a parallelogram OCEG.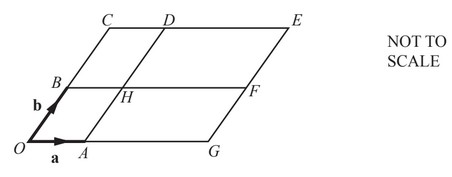
O is the origin, \(\overheadarrow{OA} = a\) and \(\overheadarrow{OB} = b\)
BHF and AHD are straight lines parallel to the sides of the parallelogram.
\(\overheadarrow{OG} = 3\overheadarrow{OA}\) and \(\overheadarrow{OC}= 2 \overheadarrow{OB}\).
(a) Write the vector \(\overheadarrow{HE}\) in terms of a and b.
\(\overheadarrow{HE}\) = …………………..
(b) Complete this statement.
a + 2b is the position vector of point …………………….
(c) Write down two vectors that can be written as 3a – b.
…………………………. and ………………………….
Answer/Explanation
Ans:
(a) 2a + b
(b) D
(c) \(\overheadarrow{CF}\) and \(\overheadarrow{BG}\)
Question
\(\begin{pmatrix}
8 &3 \\4
&2
\end{pmatrix}\)
Find
(a) A2,
Answer/Explanation
Ans: \(\begin{pmatrix}
76 &30 \\40
&16
\end{pmatrix}\)
(b) A–1.
Answer/Explanation
Ans: \(\frac{1}{4}\begin{pmatrix}
2 &-3 \\-4
&8
\end{pmatrix}oe\)
Question
Simplify.
(a) \((m^5)^2\)
(b) \(4x^3y \times 5x^2y\)
Answer/Explanation
Ans:
(a) \(m^{10}\) final answer
(b) \(20x^5y^2\) final answer
Question
M=\(\begin{pmatrix}8 & 2\\ 7 & 3\end{pmatrix}\) \(N=\begin{pmatrix}4 &-1 \\ -3 & 5\end{pmatrix}\)
(a) Find MN
(b) Find \(M^{-1}\).
Answer/Explanation
(a)\(M=\begin{pmatrix}26 & 2\\ 19 & 8\end{pmatrix}\)
(b)\(\frac{1}{10}\begin{pmatrix}3 & -2 \\ -7& 8\end{pmatrix}\)
Question
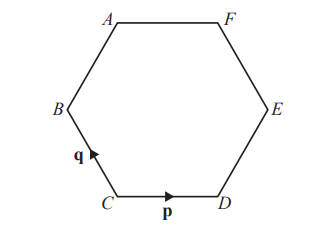
The diagram shows a regular hexagon ABCDEF.
\(\vec{CD}=p\) and\( \vec{CB}=q\)
Find CA, in terms of p and q, giving your answer in its simplest form.
Answer/Explanation
2q+p
Question
\(M=\bigl(\begin{smallmatrix}1 & & 2\\3 & & 4\end{smallmatrix}\bigr)\) \(P=\bigl(\begin{smallmatrix}5 & & 6\\7 & & 8\end{smallmatrix}\bigr)\)
(a) Find MP.
\(\begin{pmatrix}& & \\& &\end{pmatrix}\)[2]
(b) Find \(\left | M \right |\) .[1]
Answer/Explanation
Ans:
19(a) \(\begin{pmatrix}19 & 22\\43 & 50\end{pmatrix}\)
19(b) –2 final answer
Question
\(P=\begin{pmatrix}3 & & 1\\2 & & 4\end{pmatrix}\)
(a) Find P2.[2]
\(\begin{pmatrix}& & \\& &\end{pmatrix}\) [2]
(b) Find P–1.
\(\begin{pmatrix}& & \\& &\end{pmatrix}\) [2]
Answer/Explanation
Ans:
23(a) \(\begin{pmatrix}11 & & 7\\14 & & 18\end{pmatrix}\)
23(b) \(\frac{1}{10}\begin{pmatrix}4 & & -1\\-2 & & 3\end{pmatrix}\) oe isw
Question
(a) Work out \(\bigl(\begin{smallmatrix}2 & &-1 \\4& & 3\end{smallmatrix}\bigr)\) \(\bigl(\begin{smallmatrix}1 & &6 \\-5& & 4\end{smallmatrix}\bigr)\).[2]
(b) Find the value of x when the determinant o f\(\bigl(\begin{smallmatrix}3 & &-1 \\-7& & x\end{smallmatrix}\bigr)\) is 5.
x = __ [2]
Answer/Explanation
Ans:
20(a) \(\bigl(\begin{smallmatrix}7 & &8 \\-11& & 36\end{smallmatrix}\bigr)\)
20(b) 4
Question
(a)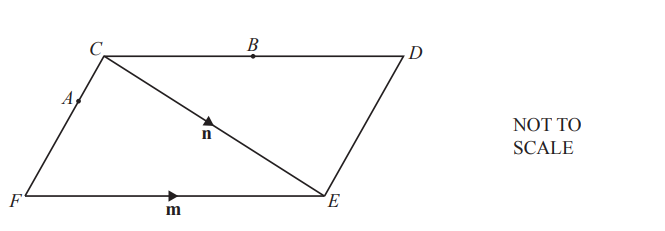
The diagram shows a parallelogram CDEF.
\(\vec{FE}=m \)and \(\vec{CE}=n.\)
B is the midpoint of CD.
FA=2AC
Find an expression ,in terms of m and n ,for \(\vec{AB}.\)
Give your answer in simplest form.
\(\vec{AB}=………………………..\)
(b)\(\vec{GH}=\frac{2}{6}(2p+q)\) \( \vec{JK}=\frac{5}{18}(2p+q)\)
Write down two factors about vectors \(\vec{GH}\) and \(\vec{JK}.\)
…………………………………………………………………………
…………………………………………………………………………
Answer/Explanation
(a)\(\frac{5}{6}m-\frac{1}{3}n\)
(b)\(\bar{GH}=3\bar{JK} \) or \(\bar{GH}\) has a greater magnitude
\(\bar{GH} \)and \(\bar{JK}\) are parallel.
Question
(a)(i)\(m=\begin{pmatrix}5\\ 7\end{pmatrix}\).Find 3m
(ii)\(\vec{VW}=\begin{pmatrix}10\\ -24\end{pmatrix}\).Find\( \left | \vec{\vec{VW}} \right |\)
……………………
(b)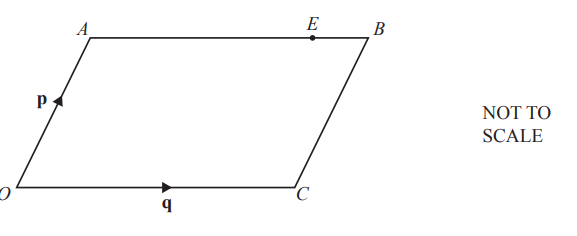
OABC is a parallelogram.
\(\vec{OA}= p\) and \(\vec{OC} = q.\)
E is the point on AB such that AE : EB = 3 : 1.
Find \(\vec{OE}\), in terms of p and q, in its simplest form.
\(\vec{OE}= …………………………………………..\)
Answer/Explanation
(a)(i)\(\begin{pmatrix}15\\ 21\end{pmatrix}\)
(ii)26
(b)\(p+\frac{3}{4}q\)
Question
Point A has coordinates (6, 4) and point B has coordinates (2, 7).
Write \(\vec{AB}\) as a column vector.
\(\vec{AB}=\left ( \right )\).
Answer/Explanation
\(\begin{pmatrix}-4\\ 3\end{pmatrix}\)
Question
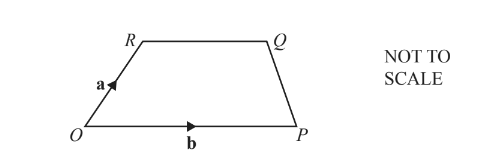
The diagram shows a trapezium OPQR.
O is the origin, \(\overrightarrow{OR}=a and \overrightarrow{OP}=b.
\left | \overrightarrow{RQ} \right |=\frac{3}{5}|\overrightarrow{OP}|\)
(a) Find \(\overrightarrow{PQ}\) in terms of a and b in its simplest form.
(b) When PQ and OR are extended, they intersect at W.
Find the position vector of W.
Answer/Explanation
(a) \(a-\frac{2}{5}b \)oe simplified
(b) \( \frac{5}{2}\)a oe
Question
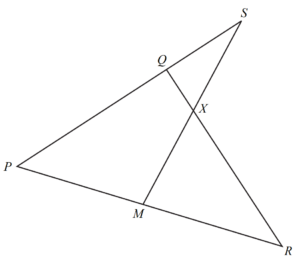
In the diagram, PQS, PMR, MXS and QXR are straight lines.
PQ = 2 QS.
M is the midpoint of P
QX : XR = 1 : 3.
\(\underset{PQ}{\rightarrow})\)=q and \(\underset{PR}{\rightarrow})\)=r.
(a) Find, in terms of q and r,
(i) \(\underset{RQ}{\rightarrow})\),
(ii) \(\underset{MS}{\rightarrow})\)
(b) By finding , show that \(\underset{MX}{\rightarrow})\) is the midpoint of MS.
Answer/Explanation
(a) (i) -r + q or q – r (ii) \(\frac{1}{2}\)(3q – r)
Question
$
\mathbf{A}=\left(\begin{array}{rr}
2 & 2 \\
2 & -2
\end{array}\right)
$
Work out
(a) $\mathbf{A}^2$,
(b) $\mathbf{A}^{-1}$, the inverse of $\mathbf{A}$.
▶️Answer/Explanation
(a) $\left(\begin{array}{ll}8 & 0 \\ 0 & 8\end{array}\right)$ oe
(b) $\left(\begin{array}{rr}\frac{1}{4} & \frac{1}{4} \\ \frac{1}{4} & -\frac{1}{4}\end{array}\right)$ oe
Question
5
$
\mathbf{A}=\left(\begin{array}{ll}
-2 & 3 \\
-4 & 5
\end{array}\right)
$
Find $\mathbf{A}^{-1}$, the inverse of the matrix $\mathbf{A}$.
▶️Answer/Explanation
$\frac{1}{2}\left(\begin{array}{ll}5 & -3 \\ 4 & -2\end{array}\right)$ or $\left(\begin{array}{cc}2.5 & -1.5 \\ 2 & -1\end{array}\right)$
Question
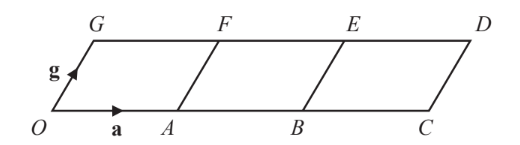
The diagram is made from three identical parallelograms.
$O$ is the origin. $\overrightarrow{O A}=\mathbf{a}$ and $\overrightarrow{O G}=\mathbf{g}$.
Write down in terms of $\mathbf{a}$ and $\mathbf{g}$
(a) $\overrightarrow{G B}$
(b) the position vector of the centre of the parallelogram BCDE.
▶️Answer/Explanation
(a) $2 \mathbf{a}-\mathbf{g}$ cao
(b) $2 \frac{1}{2} \mathbf{a}+\frac{1}{2} \mathbf{g}$ oe cao
Question
$
\mathbf{A}=\left(\begin{array}{ll}
x & 6 \\
4 & 3
\end{array}\right)
$
$
\mathbf{B}=\left(\begin{array}{ll}
2 & 3 \\
2 & 1
\end{array}\right)
$
(a) Find $\mathbf{A B}$.
(b) When $\mathbf{A B}=\mathbf{B A}$, find the value of $x$.
▶️Answer/Explanation
(a) $\left(\begin{array}{cc}2 x+12 & 3 x+6 \\ 14 & 15\end{array}\right)$
(b) 5
Question
$
\mathbf{A}=\left(\begin{array}{rr}
0 & 1 \\
-8 & -4
\end{array}\right) \quad \mathbf{B}=\left(\begin{array}{rr}
7 & 1 \\
0 & -5
\end{array}\right)
$
Calculate the value of $5|\mathbf{A}|+|\mathbf{B}|$, where $|\mathbf{A}|$ and $|\mathbf{B}|$ are the determinants of $\mathbf{A}$ and $\mathbf{B}$.
▶️Answer/Explanation
5
