iGCSE Mathematics (0580) :E7.2 Reflect simple plane figures.iGCSE Style Questions Paper 2

Question

(a)(i) \( m = \begin{pmatrix}5\\ 7\end{pmatrix} \). Find \( 3m \)

(ii) \( \vec{VW} = \begin{pmatrix}10\\ -24\end{pmatrix} \). Find \( \left| \vec{VW} \right| \)

(b)

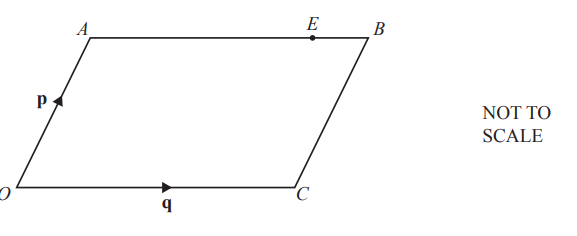
OABC is a parallelogram.

\( \vec{OA} = p \) and \( \vec{OC} = q \).

E is the point on AB such that AE : EB = 3 : 1.

Find \( \vec{OE} \), in terms of p and q, in its simplest form.

▶️ Answer/Explanation

Answer:

(a)(i) \( \begin{pmatrix}15\\ 21\end{pmatrix} \) (Multiply each component by 3).

(ii) 26 (Magnitude formula: \( \sqrt{10^2 + (-24)^2} = 26 \)).

(b) \( p + \frac{3}{4}q \) (Since AB = q and E divides AB in a 3:1 ratio, \( \vec{OE} = \vec{OA} + \frac{3}{4}\vec{AB} \)).

Question

Point A has coordinates (6, 4) and point B has coordinates (2, 7). Write \(\vec{AB}\) as a column vector.

\(\vec{AB}=\left ( \right )\).

▶️ Answer/Explanation

Answer: \(\begin{pmatrix}-4\\ 3\end{pmatrix}\)

Subtract A’s coordinates from B’s: (2-6, 7-4) = (-4, 3). The column vector represents this change in x and y.

Resources