Question
Find the matrix which represents the combined transformation of a reflection in the x axis followed by a reflection in the line y = x.
Answer/Explanation
Ans: \(\begin{pmatrix}0 &-1 \\1 &0 \end{pmatrix}cao\)
Question
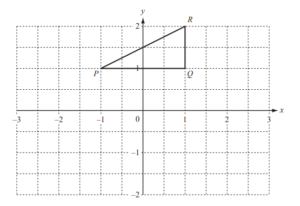
The triangle PQR has co-ordinates P(O1, 1), Q(1, 1) and R(1, 2).
(a) Rotate triangle PQR by 90° clockwise about (0, 0).
Label your image P’Q’R’.
Answer/Explanation
Ans: triangle at (1, 1), (1, –1), (2, –1)
(b) Reflect your triangle P’Q’R’ in the line y = − x .
Label your image P”Q”R”.
Answer/Explanation
Ans: triangle at (–1, –1)(1, –1), (1, –2)
(c) Describe fully the single transformation which maps triangle PQR onto triangle P”Q”R”.
Answer/Explanation
Ans: reflection in the x axis
Question
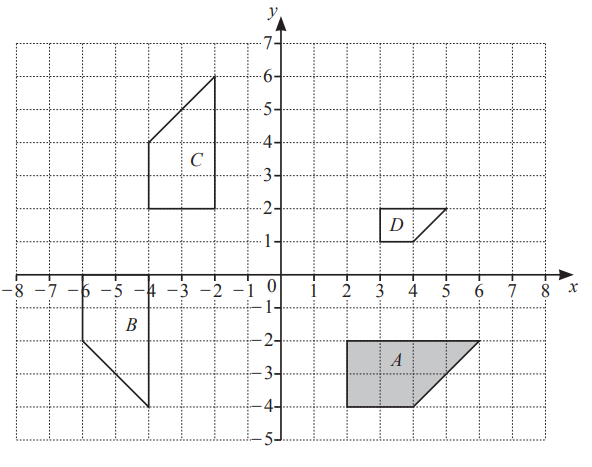
(a) Describe fully the single transformation that maps triangle S onto triangle T.
Answer/Explanation
Ans: Enlargement
\(\frac{1}{2}\)
origin oe
(b) Find the matrix which represents the transformation that maps triangle S onto triangle T.
Answer/Explanation
Ans: \(\begin{pmatrix}\frac{1}{2} &0 \\0 &\frac{1}{2} \end{pmatrix} oe\)
Question
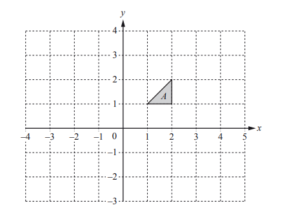
Draw the image of shape A after a translation by the vector \(\binom{2}{-3}.\)
Answer/Explanation
Ans: Triangle (3, –2), (4, –2), (4, –1)
Question
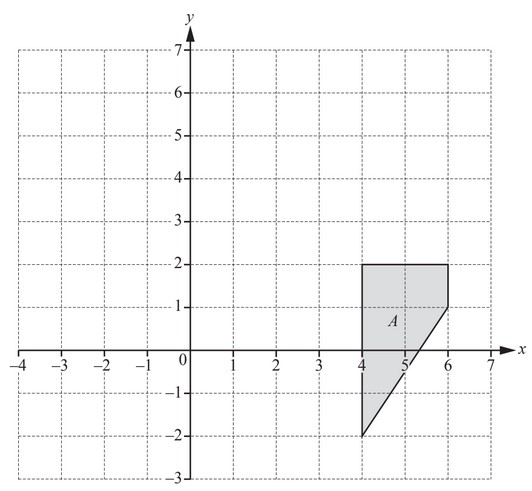
T(X) is the image of the shape X after translation by the vector \(\begin{pmatrix}
-1\\3
\end{pmatrix}\)
M(Y) is the image of the shape Y after reflection in the line x = 2.
On the grid, draw MT(A), the image of shape A after the transformation MT.
Answer/Explanation
Ans:
Question
The diagram shows a parallelogram OCEG.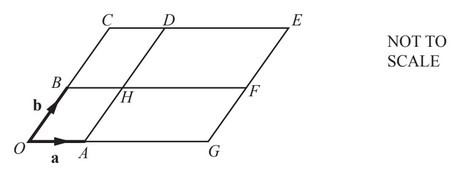
O is the origin, \(\overheadarrow{OA} = a\) and \(\overheadarrow{OB} = b\)
BHF and AHD are straight lines parallel to the sides of the parallelogram.
\(\overheadarrow{OG} = 3\overheadarrow{OA}\) and \(\overheadarrow{OC}= 2 \overheadarrow{OB}\).
(a) Write the vector \(\overheadarrow{HE}\) in terms of a and b.
\(\overheadarrow{HE}\) = …………………..
(b) Complete this statement.
a + 2b is the position vector of point …………………….
(c) Write down two vectors that can be written as 3a – b.
…………………………. and ………………………….
Answer/Explanation
Ans:
(a) 2a + b
(b) D
(c) \(\overheadarrow{CF}\) and \(\overheadarrow{BG}\)
Question
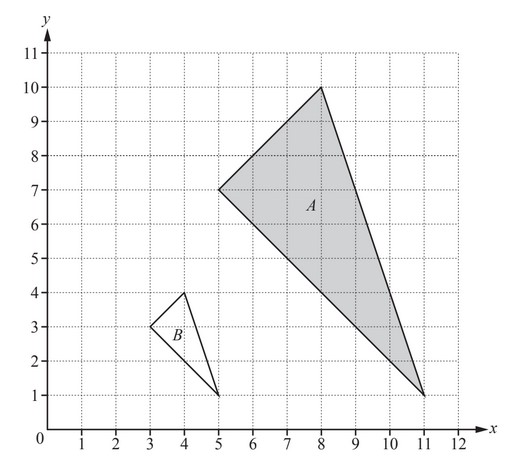
Describe fully the single transformation that maps triangle A onto triangle B.
Answer/Explanation
Ans:
Enlargement
\(\frac{1}{3}\)
(2, 1)
Question
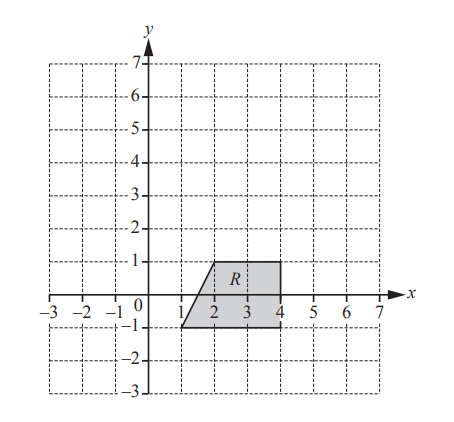
On the grid, draw the image of shape R after the transformation represented by the matrix \begin{pmatrix}0 & -1\\ 1 & 0\end{pmatrix}.
Answer/Explanation
Shape with vertices at
(1, 1), (1, 4), (−1, 2), (−1, 4)
Question
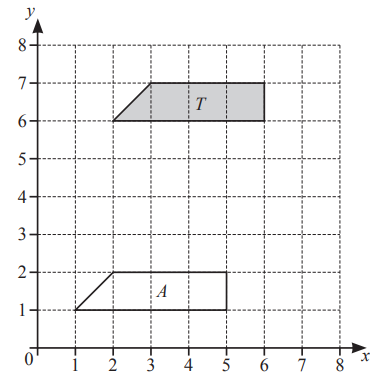
(a) Describe fully the single transformation that maps shape T onto shape A.[2]
(b) On the grid, reflect shape T in the line y = x. [2]
Answer/Explanation
Ans:
21(a) Translation
\(\binom{-1}{-5}\)
21(b) Correct reflection at
(6, 2), (6, 6), (7, 6), (7, 3)
Question
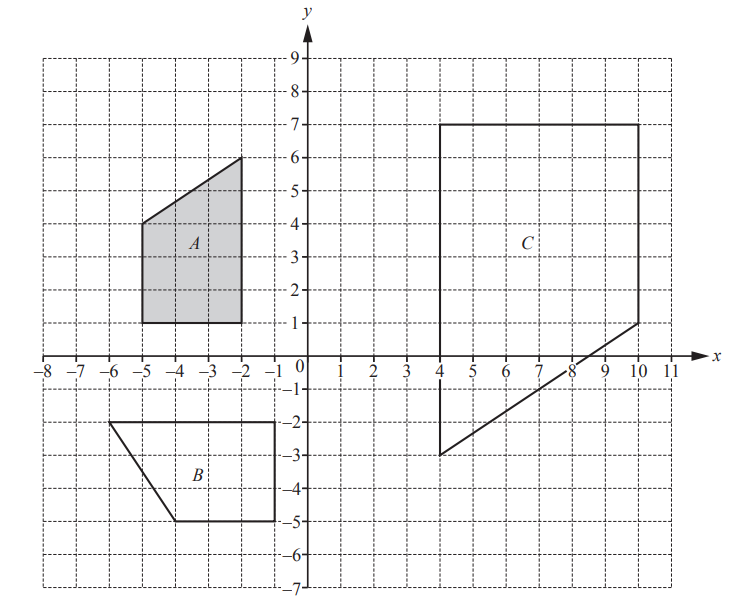
Describe fully the single transformation that maps
(a) shape A onto shape B,
…………………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………………..
(b) shape A onto shape C.
…………………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………………..
Answer/Explanation
(a) Rotation
cenrtre origin
\(90^{\circ}\) anti-clcokwise
(b)Enlargement
centre (0,3)
sf -2
Question
Describe fully the single transformation that maps
(a) shape A onto shape B,
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
(b) shape A onto shape C,
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
(c) shape A onto shape D.
…………………………………………………………………………………………………………………………………..
…………………………………………………………………………………………………………………………………..
Answer/Explanation
(a)Rotation
90° clockwise oe
(0, 2)
(b)Reflection
y = x
(c) Enlargement
\([sf] \frac{1}{2}\)
(4, 6)
Question
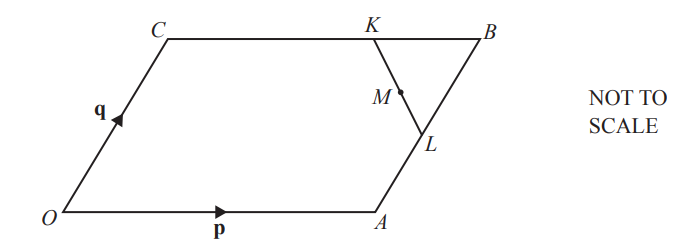
OABC is a parallelogram and O is the origin.
CK = 2KB and AL = LB.
M is the midpoint of KL.
\(\underset{OA}{\rightarrow}\) = p and \(\underset{OC}{\rightarrow}\)= q.
Find, in terms of p and q, giving your answer in its simplest form
(a) \(\underset{KL}{\rightarrow}\),
\(\underset{KL}{\rightarrow}\) = [2]
(b) the position vector of M. [2]
Answer/Explanation
Ans:
25(a) \(\frac{1}{3}p-\frac{1}{2}q\) oe simplified
25(b) \(\frac{5}{6}p-\frac{3}{4}q\) oe simplified
Question
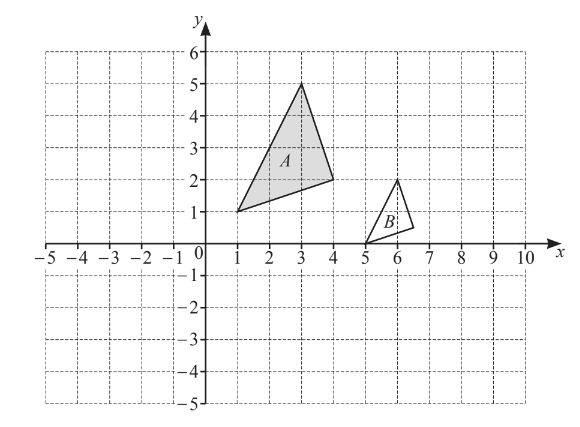
(a) On the grid, draw the image of
(i) triangle A after a reflection in the y-axis,
(ii) triangle A after a translation by the vector
\(\binom{-3}{-4}\)
(b) Describe fully the single transformation that maps triangle A onto triangle B.
Answer/Explanation
(a)(i) triangle at (− 1, 1) (− 4, 2) (− 3, 5)
(a)(ii) triangle at (− 2, −3) (1, − 2) (0, 1)
(b) enlargement
\([sf]\frac{1}{2}\)
[centre] (9, − 1)
Question
Work out.
(a)\({\bigl(\begin{smallmatrix}
2 & 1 & \\
4& 3&
\end{smallmatrix}\bigr)}^2\)
(b)\({\bigl(\begin{smallmatrix}
2 & 1 & \\
4& 3&
\end{smallmatrix}\bigr)}^{-1}\)
Answer/Explanation
(a) \({\bigl(\begin{smallmatrix}
2 & 1 & \\
4& 3&
\end{smallmatrix}\bigr)}^2\)
On multiplying ,we get,
\(=\bigl(\begin{smallmatrix}
4+4& 2+3 & \\
8+12& 4+9&
\end{smallmatrix}\bigr)\)
\(=\bigl(\begin{smallmatrix}8& 5 & \\
20& 13&
\end{smallmatrix}\bigr)\)
(b) \({\bigl(\begin{smallmatrix}
2 & 1 & \\
4& 3&
\end{smallmatrix}\bigr)}^{-1}\)
\(A^{-1}=\frac{1}{|A|}\bigl(\begin{smallmatrix}2 & 1 & \\
4& 3&
\end{smallmatrix}\bigr)\)
|A|=\(a_4.a_1-a_2.a_3\)
|A|=6-4=2
Now , putting into equation, invrse :
\(A^{-1}=\frac{1}{2}\bigl(\begin{smallmatrix}3 & -1 & \\
-4& 2&
\end{smallmatrix}\bigr)\)(Interchanging places of\(a_1\) and \(a_4\) and reversing signs of \(a_2\) and \(a_3)\)
Question
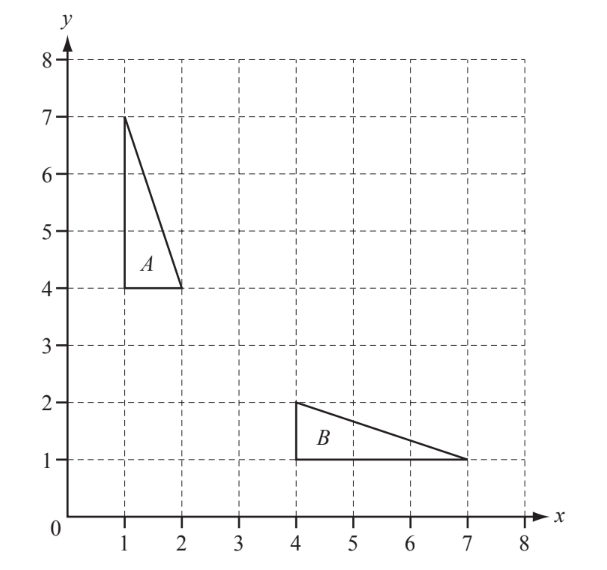
(a) Describe fully the single transformation which maps triangle $A$ onto triangle $B$.
(b) On the grid, draw the image of triangle $A$ after rotation by $90^{\circ}$ clockwise about the point $(4,4)$.
▶️Answer/Explanation
(a) Reflection in $y=x$
(b) Triangle at $(4,6),(4,7),(7,7)$