(a) \( p = \begin{pmatrix} 2 \\ 3 \end{pmatrix} \) \( q = \begin{pmatrix} -1 \\ 1 \end{pmatrix} \)
Find
(i) 3q,
(ii) \( p – q \),
(iii) \( |p| \).
(b) B is the point (2, 7) and \( \overrightarrow{AB} = \begin{pmatrix} -4 \\ 6 \end{pmatrix} \).
Find the coordinates of A.
(c) 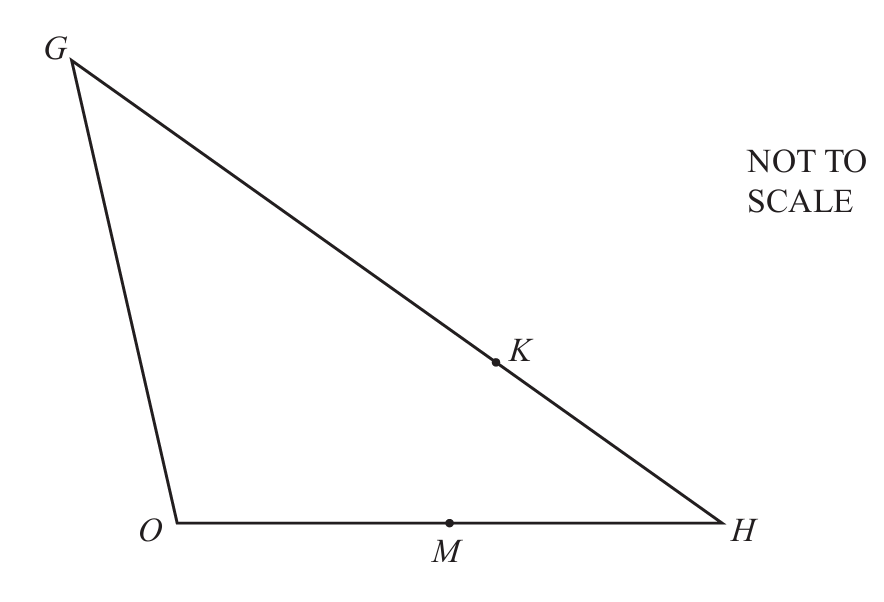
In triangle OGH, M is the midpoint of OH and K divides GH in the ratio 5:2.
\( \overrightarrow{OG} = g \) and \( \overrightarrow{OH} = h \).
Find \( \overrightarrow{MK} \) in terms of g and h.
Give your answer in its simplest form.
▶️ Answer/Explanation
(a)(i) \( \begin{pmatrix} -3 \\ 3 \end{pmatrix} \)
Multiply each component of q by 3: \( 3 \times \begin{pmatrix} -1 \\ 1 \end{pmatrix} = \begin{pmatrix} -3 \\ 3 \end{pmatrix} \).
(a)(ii) \( \begin{pmatrix} 3 \\ 2 \end{pmatrix} \)
Subtract corresponding components: \( \begin{pmatrix} 2-(-1) \\ 3-1 \end{pmatrix} = \begin{pmatrix} 3 \\ 2 \end{pmatrix} \).
(a)(iii) 3.61 or \( \sqrt{13} \)
Use the magnitude formula: \( \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} \approx 3.61 \).
(b) (6, 1)
To find A, subtract the vector AB from B’s coordinates: \( (2 – (-4), 7 – 6) = (6, 1) \).
(c) \( \frac{2}{7}g + \frac{3}{14}h \)
First find M (midpoint of OH): \( \frac{h}{2} \). Then find K’s position: \( g + \frac{5}{7}(h – g) \). Finally, \( \overrightarrow{MK} = K – M = \frac{2}{7}g + \frac{3}{14}h \).
(a) ABC is a triangle.
B is the point (1, -10), A is the point (4, 14) and \(\overrightarrow{CA} = \begin{pmatrix} -11 \\ 8 \end{pmatrix}\).
(i) Find the coordinates of C.
(ii) Find \(\overrightarrow{BA}\).
(iii) Find \(|\overrightarrow{CA}\|).
(b) 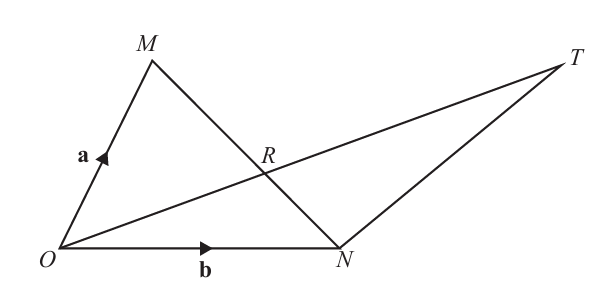
OMN is a triangle.
\(\overrightarrow{OM} = \mathbf{a}\) and \(\overrightarrow{ON} = \mathbf{b}\).
R is a point on MN such that MR : RN = 3 : 2.
ORT is a straight line.
(i) Show that \(\overrightarrow{OR} = \frac{2}{5} \mathbf{a} + \frac{3}{5} \mathbf{b}\).
(ii) (a) \(\overrightarrow{NT} = 4\mathbf{a} + k\mathbf{b}\) and \(\overrightarrow{OT} = c \overrightarrow{OR}\).
Find the value of k and the value of c.
(b) Find \(\overrightarrow{MT}\).
▶️ Answer/Explanation
(a)(i) (15, 6)
To find C, add \(\overrightarrow{CA}\) to A’s coordinates: (4 + (-11), (14 + (-8)) = (-7, 6). Wait no, actually \(\overrightarrow{CA}\) is A-C, so C = A – \(\overrightarrow{CA}\) = (4 – (-11), (14 – 8) = (15, 6).
(a)(ii) \(\begin{pmatrix} 3 \\ 24 \end{pmatrix}\)
\(\overrightarrow{BA}\) is A – B = (4-1, 14-(-10)) = (3, 24).
(a)(iii) 13.6 or 13.60…
Magnitude of \(\overrightarrow{CA}\) is \(\sqrt{(-11)^2 + 8^2} = \sqrt{121 + 64} = \sqrt{185} ≈ 13.6\).
(b)(i)
Since MR:RN = 3:2, R divides MN in ratio 3:2. Using section formula: \(\overrightarrow{OR} = \frac{2}{5}\mathbf{a} + \frac{3}{5}\mathbf{b}\).
(b)(ii)(a) k = 5, c = 10
Given \(\overrightarrow{OT} = c\overrightarrow{OR} = c(\frac{2}{5}\mathbf{a} + \frac{3}{5}\mathbf{b})\). Also \(\overrightarrow{OT} = \overrightarrow{ON} + \overrightarrow{NT} = \mathbf{b} + 4\mathbf{a} + k\mathbf{b}\).
Equating coefficients: \(\frac{2}{5}c = 4 ⇒ c=10\), and \(\frac{3}{5}c = 1+k ⇒ k=5\).
(b)(ii)(b) \(3\mathbf{a} + 6\mathbf{b}\)
\(\overrightarrow{MT} = \overrightarrow{MO} + \overrightarrow{OT} = -\mathbf{a} + 10(\frac{2}{5}\mathbf{a} + \frac{3}{5}\mathbf{b}) = 3\mathbf{a} + 6\mathbf{b}\).
