(a) Find the magnitude of the vector \(\begin{pmatrix}-4 \\ 5\end{pmatrix}\).
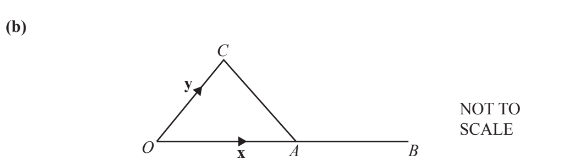
The diagram shows a triangle OAC.
A is the midpoint of the straight line OB.
\(\vec{OA} = x\) and \(\vec{OC} = y\).
Find \(\vec{CB}\) in terms of \(x\) and \(y\).
▶️ Answer/Explanation
(a) Ans: \(\sqrt{41}\) or \(6.40\)
Magnitude of \(\begin{pmatrix}-4 \\ 5\end{pmatrix}\) is calculated using \(\sqrt{(-4)^2 + 5^2} = \sqrt{16 + 25} = \sqrt{41}\).
\(\sqrt{41} \approx 6.40\) (to 2 decimal places).
(b) Ans: \(2x – y\)
Since \(A\) is the midpoint of \(OB\), \(\vec{OB} = 2x\).
Using vector subtraction: \(\vec{CB} = \vec{OB} – \vec{OC} = 2x – y\).

$O$ is the origin and $OPQR$ is a parallelogram.
$M$ is the midpoint of $PQ$ and $N$ divides $\overrightarrow{OR}$ in the ratio 2:1.
$\overrightarrow{OP}=\mathbf{a}$ and $\overrightarrow{OR}=\mathbf{b}$.
(a) Find $\overrightarrow{MN}$.
Give your answer in terms of $\mathbf{a}$ and/or $\mathbf{b}$ and in its simplest form.
(b) The lines $MN$ and $OR$ are extended to meet at $S$.
Find the position vector of $S$.
Give your answer in terms of $\mathbf{a}$ and/or $\mathbf{b}$ and in its simplest form.
▶️ Answer/Explanation
(a) Ans: $\frac{1}{2}\mathbf{b}-\frac{2}{3}\mathbf{a}$
1. Since $OPQR$ is a parallelogram, $\overrightarrow{OQ} = \overrightarrow{OP} + \overrightarrow{OR} = \mathbf{a} + \mathbf{b}$.
2. The midpoint $M$ of $PQ$ has position vector: $\overrightarrow{OM} = \overrightarrow{OP} + \frac{1}{2}\overrightarrow{PQ} = \mathbf{a} + \frac{1}{2}\mathbf{b}$.
3. Point $N$ divides $OR$ in 2:1 ratio: $\overrightarrow{ON} = \frac{2}{3}\mathbf{b}$.
4. Therefore, $\overrightarrow{MN} = \overrightarrow{ON} – \overrightarrow{OM} = \frac{2}{3}\mathbf{b} – (\mathbf{a} + \frac{1}{2}\mathbf{b}) = \frac{1}{2}\mathbf{b} – \frac{2}{3}\mathbf{a}$.
(b) Ans: $\frac{5}{4}\mathbf{b}$
1. The line $MN$ can be parameterized as $\mathbf{r} = \overrightarrow{OM} + t\overrightarrow{MN} = (\mathbf{a} + \frac{1}{2}\mathbf{b}) + t(\frac{1}{2}\mathbf{b} – \frac{2}{3}\mathbf{a})$.
2. The line $OR$ is simply $\mathbf{r} = s\mathbf{b}$.
3. At intersection point $S$, we equate components:
- $\mathbf{a}$ component: $1 – \frac{2}{3}t = 0 \Rightarrow t = \frac{3}{2}$
- $\mathbf{b}$ component: $\frac{1}{2} + \frac{1}{2}t = s$
4. Substituting $t = \frac{3}{2}$ gives $s = \frac{1}{2} + \frac{1}{2}(\frac{3}{2}) = \frac{5}{4}$.
5. Thus, the position vector of $S$ is $\frac{5}{4}\mathbf{b}$.
