Question
(a) A sample of sand has a volume of 0.050m3. The density of the sand is 1900kg/m3. The specific heat capacity of the sand is 1500J /(kg °C).
(i) Calculate the mass of the sample of sand.
mass = [2]
(ii) Calculate the thermal capacity of the sample of sand.
thermal capacity = [2]
(iii) The initial temperature of the sample of sand is 7.0°C. The sample of sand is heated using an electrical heater. The power of the heating element is 50W.
Calculate the time taken to increase the temperature of the sand to 19.0°C.
time = [3]
(b) In some countries, the soil is too cold for plants to grow well. In these countries, plants are grown in plastic pots and kept inside. The pots, containing soil, are placed on sand. The sand is heated using an electrical heater, as shown in Fig. 4.1.
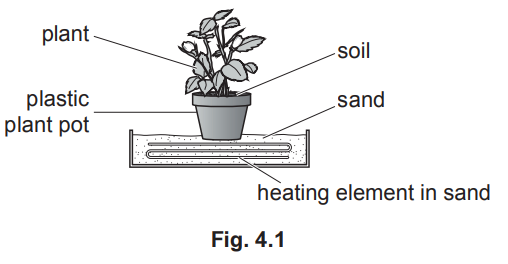
(i) Describe, in terms of molecules, how thermal energy is transferred from the heated sand through the base of the plastic pot. [2]
(ii) The heating element in Fig. 4.1 remains switched on. The temperature of the sand remains constant at a value above room temperature.
Explain why the temperature of the sand remains constant.[2] [Total: 11]
Answer/Explanation
Ans:
(a)(i) (mass = 1900 × 0.05) = 95 kg
(m =) ρV in any form OR 1900 × 0.05
(a)(ii) (= 95 × 1500) = 140 000 J / °C / 1.4 × 105 J / °C A2
(C =) m x c
(a)(iii) 34 000 s / 560 min / 9 h 20 min
Temperature rise = 12(°C) / 19–7
OR
E = C × Δ θ in any form
(t =) E / P in any form OR (thermal capacity × 12) / 50
(b)(i) sand molecules gain KE OR vibrate more OR hit (other) molecules (when heated)
OR
(thermal energy is transferred by) conduction
Energy is transferred to molecules of plastic pot in contact with sand (through collisions)
OR
Energy OR (lattice) vibrations transferred to neighbouring molecules
(b)(ii) (sand is warmer than surroundings and so thermal) energy (constantly) is lost from the sand
(at a constant temperature) rate of (thermal) energy supplied to the sand is equal to rate of (thermal) energy lost from sand
Question
A steel object has 5 kg stamped on its side, as shown in Fig. 2.1.
(a) Express 5.0 kg in grams. 5.0 kg = …………………………………….. g
(b) The density of the steel is 7.81 g / \(cm^3\).
Calculate the volume of the object.
volume = …………………………………. \(cm^3\)
Answer/Explanation
Answer:
(a) 5000 (g)
(b) density = mass / volume in any form OR (volume =) mass / density
5000/ 7.81 OR 5 / 7.81 OR 0.64, ecf from (a)
640(\(cm^3\)), accept 6.4 × \(10^{-4}\) if clearly stated in \(m^3\)
