Question
Fig. 3.1 shows the descent of a sky-diver from a stationary balloon.
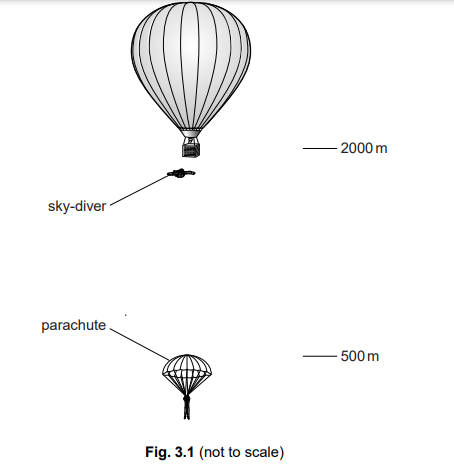
The sky-diver steps from the balloon at a height of 2000 m and accelerates downwards.
His speed is 52 m / s at a height of 500 m.
He then opens his parachute. From 400 m to ground level, he falls at constant speed.
(a) The total mass of the sky-diver and his equipment is 92 kg.
(i) Calculate, for the sky-diver,
1) the loss of gravitational potential energy in the fall from 2000 m to 500 m,
loss of gravitational potential energy =……………………………………………………..
2) the kinetic energy at the height of 500 m.
kinetic energy =……………………………………………………….
(ii) The kinetic energy at 500 m is not equal to the loss of gravitational potential energy.
Explain why there is a difference in the values.
(b) State
(i) what happens to the air resistance acting on the sky-diver during the fall from 2000 m to 500 m,
………………………………………………………………………………………………………………
(ii)the value of the air resistance during the fall from 400 m to ground.
air resistance =…………………………………………..
Answer/Explanation
Answer:
(a) (i) 1. (loss of P.E. =) mgh OR 92 × 10 × 1500 1.38 × \(10^6\) J correct use of mgh with h = 500 or 2000 gains 1 mark only
(ii) 2. (K.E. =) ½ \(mv^2\) OR ½ × 92 × \(52^2\) 1.244 × \(10^2\) J at least 2 sig. figs
(iii) difference is due to: (work done in overcoming) air resistance/drag OR energy converted to/lost as heat (by air resistance/drag)
(b) (i) increases
(ii) 920 N
Question
A diver climbs some steps on to a fixed platform above the surface of the water in a swimming-pool.
He dives into the pool. Fig. 2.1 shows the diver about to enter the water.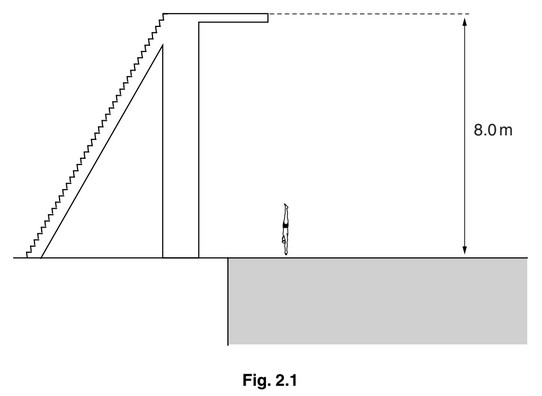
The mass of the diver is 65 kg. The platform is 8.0 m above the surface of the water.
(a) Calculate
(i) the increase in the gravitational potential energy of the diver when he climbs up to the
platform.
increase in gravitational potential energy =
(ii) the speed with which the diver hits the surface of the water. Ignore any effects of air
resistance.
speed =
(b) In another dive from the same platform, the diver performs a somersault during the descent.
He straightens, and again enters the water as shown in Fig. 2.1.
Discuss whether the speed of entry into the water is greater than, less than or equal to the
speed calculated in (a)(ii). Ignore any effects of air resistance.
Answer/Explanation
Answer:
(a) (i) (increase in g.p.e. = mgh OR 65 × 10 × 8 =) 5200J
(ii) EITHER
k.e. gained = g.p.e. lost
1⁄2 \(mv^2\) = 5200 in any form
\(v^2\) = 5200/(0.5 × 65) OR 160
v = 12.6m/ s e.c.f. (a)(i)
OR
\(v^2 = u^2 + 2as / v^2 = 2 gh\)
\(v^2 = 2 × 10 × 8\)
\(v^2\) = 160
v = 12.6m/ s e.c.f. (a)(i)
(b) speed is the same
EITHER
loss in g.p.e. is the same
k.e. gained is the same
OR
acceleration is the same
distance fallen is the same
