CIE IGCSE Mathematics (0580) Non-right-angled Triangles Study Notes - New Syllabus
CIE IGCSE Mathematics (0580) Non-right-angled Triangles Study Notes
LEARNING OBJECTIVE
- Non-Right-Angled Triangles
Key Concepts:
- Non-Right-Angled Triangles
Non-Right-Angled Triangles
Non-Right-Angled Triangles
For triangles that do not contain a right angle, we use the Sine Rule and the Cosine Rule to calculate unknown angles and sides.
1. Sine Rule
The sine rule is used when you are given either:
- Two angles and one side (AAS or ASA)
- Two sides and a non-included angle (SSA)
Formula:
\( \dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} \)
Where \( a, b, c \) are sides opposite angles \( A, B, C \) respectively.
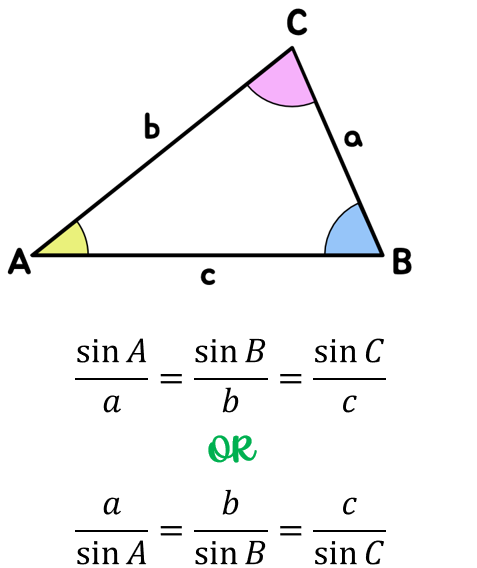
Example:
In triangle ABC, \( a = 7 \) cm, \( A = 40^\circ \), and \( B = 65^\circ \). Find side \( b \).
▶️ Answer/Explanation
First find angle \( C = 180^\circ – 40^\circ – 65^\circ = 75^\circ \)
Use the sine rule: \( \dfrac{a}{\sin A} = \dfrac{b}{\sin B} \)
\( \dfrac{7}{\sin 40^\circ} = \dfrac{b}{\sin 65^\circ} \)
\( b = \dfrac{7 \cdot \sin 65^\circ}{\sin 40^\circ} \approx \dfrac{7 \cdot 0.9063}{0.6428} \approx \boxed{9.87 \text{ cm}} \)
2. Cosine Rule
The cosine rule is used when you are given:
- Two sides and the included angle (SAS)
- All three sides (SSS)
Formulas for finding a side:
- \( a^2 = b^2 + c^2 – 2bc \cos A \)
- \( b^2 = a^2 + c^2 – 2ac \cos B \)
- \( c^2 = a^2 + b^2 – 2ab \cos C \)
Formulas for finding an angle:
- \( \cos A = \dfrac{b^2 + c^2 – a^2}{2bc} \)
- \( \cos B = \dfrac{a^2 + c^2 – b^2}{2ac} \)
- \( \cos C = \dfrac{a^2 + b^2 – c^2}{2ab} \)
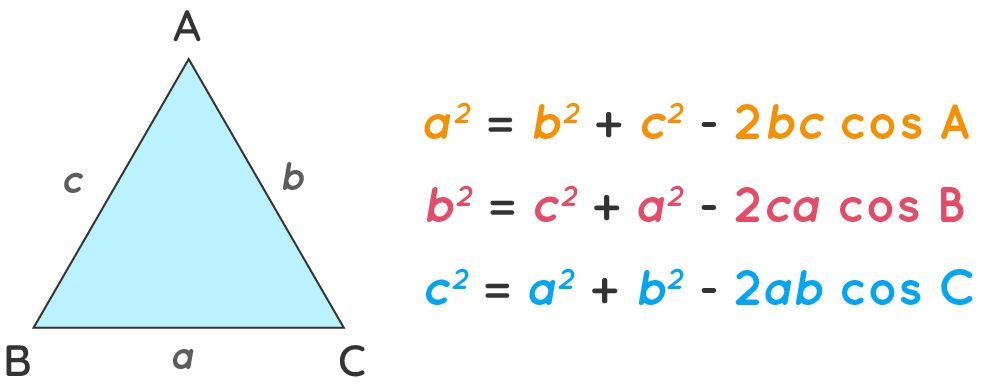
Example:
In triangle PQR, \( PQ = 8 \) cm, \( PR = 6 \) cm, and \( \angle QPR = 60^\circ \). Find side \( QR \).
▶️ Answer/Explanation
Use cosine rule: \( QR^2 = PQ^2 + PR^2 – 2(PQ)(PR)\cos \angle QPR \)
\( QR^2 = 8^2 + 6^2 – 2(8)(6)\cos 60^\circ \)
\( = 64 + 36 – 96 \cdot 0.5 = 100 – 48 = 52 \)
\( QR = \sqrt{52} \approx \boxed{7.21 \text{ cm}} \)
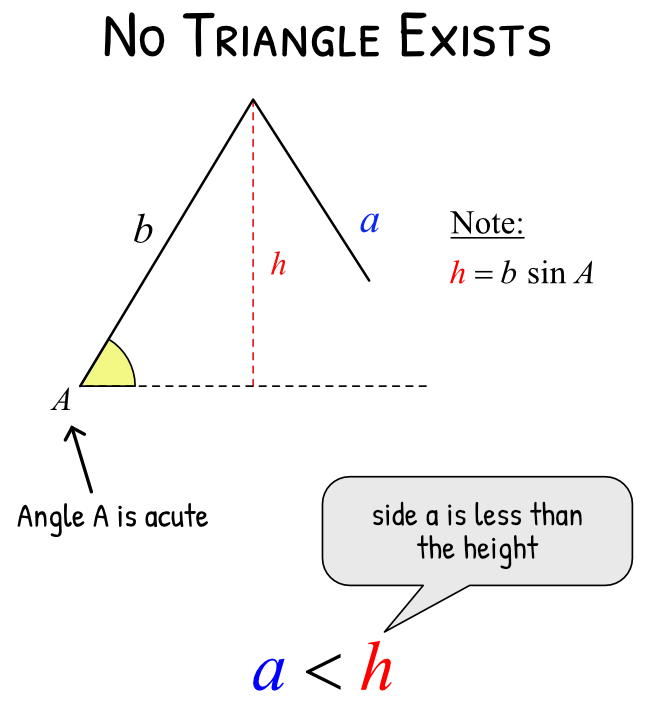
3. Obtuse Angles and Ambiguous Case (SSA)
When using the sine rule with two sides and a non-included angle (SSA), there may be:
0 solutions – when the given side is too short

1 solution – when the triangle is unique
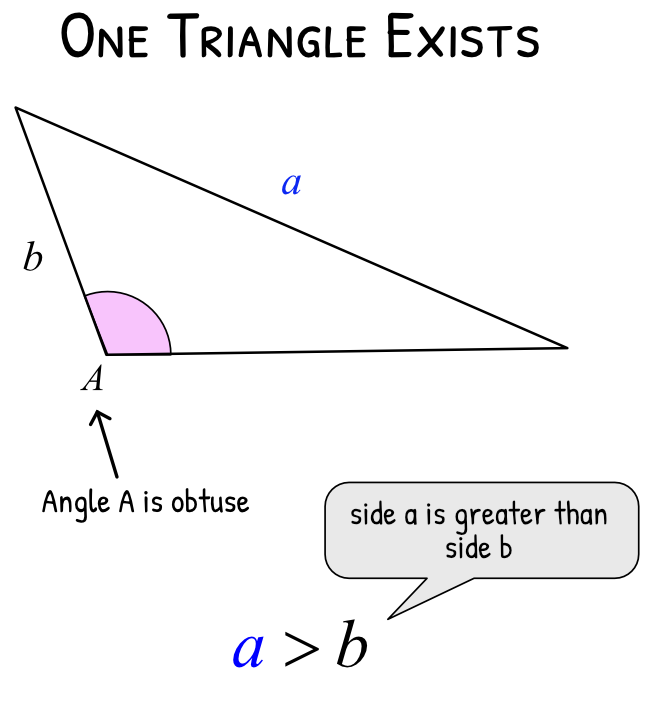
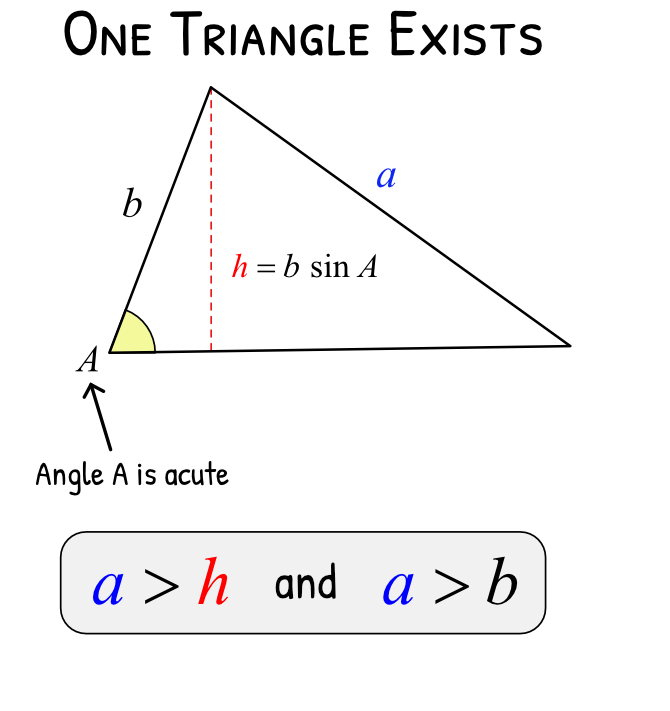
2 solutions – when two different triangles can be formed (ambiguous case)
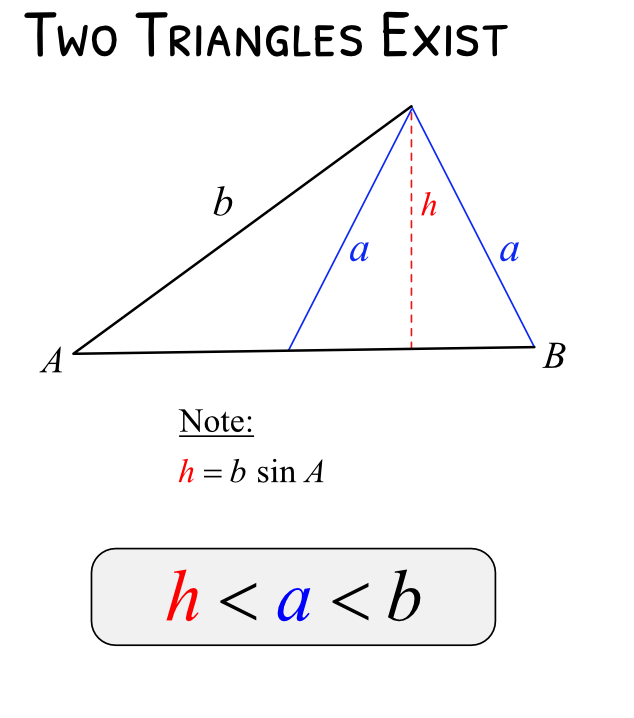
Example :
In triangle XYZ, \( x = 10 \) cm, \( y = 12 \) cm, and \( \angle X = 40^\circ \). Determine how many triangles can be formed.
▶️ Answer/Explanation
Use the sine rule to find angle \( Y \):
\( \dfrac{10}{\sin 40^\circ} = \dfrac{12}{\sin Y} \Rightarrow \sin Y = \dfrac{12 \cdot \sin 40^\circ}{10} \approx \dfrac{12 \cdot 0.6428}{10} \approx 0.7714 \)
Now find angle \( Y = \sin^{-1}(0.7714) \approx 50.4^\circ \)
Two possibilities: \( Y = 50.4^\circ \) or \( Y = 129.6^\circ \) (since \( \sin \theta = \sin(180^\circ – \theta) \))
In both cases, angle \( Z \) will still be positive, so two triangles are possible.
Area of a Triangle using Sine Rule
Area of a Triangle using Sine Rule
For any triangle (not necessarily right-angled), you can calculate the area using the formula:
$\text{Area} = \frac{1}{2} ab \sin C $
Here, \( a \) and \( b \) are two sides of the triangle, and \( C \) is the angle between them.

Example:
Find the area of a triangle with sides \( a = 8 \) cm, \( b = 10 \) cm, and included angle \( C = 35^\circ \).
▶️ Answer/Explanation
Use the formula: \( \text{Area} = \dfrac{1}{2} ab \sin C \)
\( = \dfrac{1}{2} \cdot 8 \cdot 10 \cdot \sin 35^\circ \)
\( = 40 \cdot \sin 35^\circ \approx 40 \cdot 0.574 \approx \boxed{22.96 \text{ cm}^2} \)
Example:
In triangle XYZ, side \( XY = 13 \) cm, side \( YZ = 15 \) cm, and angle \( \angle XYZ = 110^\circ \). Find the area of the triangle.
▶️ Answer/Explanation
Apply: \( \text{Area} = \dfrac{1}{2} ab \sin C \)
\( = \dfrac{1}{2} \cdot 13 \cdot 15 \cdot \sin 110^\circ \)
\( \approx 97.5 \cdot \sin 110^\circ \approx 97.5 \cdot 0.9397 \approx \boxed{91.63 \text{ cm}^2} \)
