Units of Measure and Conversions

Metric units are used to measure length, area, volume, capacity, and mass. 

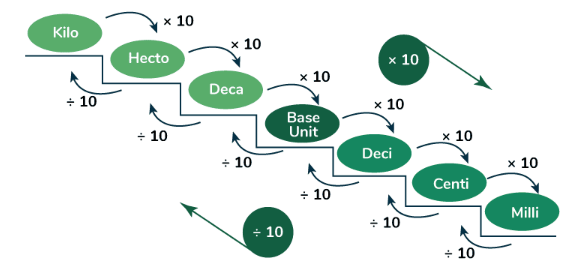
1. Length Units

• 1 kilometre (km) = 1000 metres (m)
• 1 metre (m) = 100 centimetres (cm)
• 1 centimetre (cm) = 10 millimetres (mm)

Conversions: \( 1 \text{ km} = 1000 \text{ m}, \quad 1 \text{ m} = 100 \text{ cm}, \quad 1 \text{ cm} = 10 \text{ mm} \)

2. Area Units

• 1 m² = 10,000 cm²
• 1 cm² = 100 mm²
• 1 km² = 1,000,000 m²

Conversions: \( 1 \text{ m}^2 = 10,000 \text{ cm}^2, \quad 1 \text{ cm}^2 = 100 \text{ mm}^2, \quad 1 \text{ km}^2 = 1,000,000 \text{ m}^2 \)

3. Volume Units

• 1 m³ = 1,000,000 cm³
• 1 cm³ = 1000 mm³

Conversions: \( 1 \text{ m}^3 = 1,000,000 \text{ cm}^3, \quad 1 \text{ cm}^3 = 1000 \text{ mm}^3 \)

4. Capacity (Liquid Volume)

• 1 litre (L) = 1000 millilitres (ml)
• 1 cm³ = 1 ml
• 1000 cm³ = 1 L

Conversions: \( 1 \text{ L} = 1000 \text{ ml}, \quad 1 \text{ cm}^3 = 1 \text{ ml} \)

5. Mass Units

• 1 kilogram (kg) = 1000 grams (g)
• 1 gram (g) = 1000 milligrams (mg)

Conversions: \( 1 \text{ kg} = 1000 \text{ g}, \quad 1 \text{ g} = 1000 \text{ mg} \)

Tips for Conversion:

• To convert to a larger unit, divide.
• To convert to a smaller unit, multiply.
• Always write the correct unit and check if the final value makes sense.

Conversions Between Area Units

Area units increase by powers of 100 (not 10), because area involves length × width.

• \( 1 \text{ m}^2 = 10,000 \text{ cm}^2 \)
• \( 1 \text{ cm}^2 = 100 \text{ mm}^2 \)
• \( 1 \text{ km}^2 = 1,000,000 \text{ m}^2 \)

Conversions Between Volume and Capacity

Volume and capacity are directly related: \( 1 \text{ cm}^3 = 1 \text{ ml}, \quad 1000 \text{ cm}^3 = 1 \text{ litre}, \quad 1 \text{ m}^3 = 1000 \text{ litres} \)

• \( 1 \text{ litre} = 1000 \text{ cm}^3 \)
• \( 1 \text{ m}^3 = 1000 \text{ litres} \)
• \( 1 \text{ cm}^3 = 1 \text{ ml} \)