CIE IGCSE Mathematics (0580) Vector geometry Study Notes - New Syllabus
CIE IGCSE Mathematics (0580) Vector geometry Study Notes
LEARNING OBJECTIVE
- Vector Reasoning in Geometry
Key Concepts:
- Vector Reasoning in Geometry
Vector Reasoning in Geometry
A. Showing Vectors are Parallel
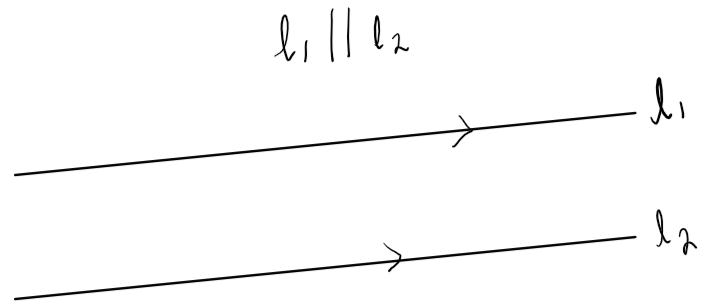
Two vectors are parallel if one is a scalar multiple of the other.
e.g. \( \vec{a} = \begin{pmatrix} 2 \\ 6 \end{pmatrix} \), \( \vec{b} = \begin{pmatrix} 1 \\ 3 \end{pmatrix} \), then \( \vec{a} = 2 \cdot \vec{b} \), so they are parallel.
Example:
Are the vectors \( \vec{p} = \begin{pmatrix} 4 \\ 8 \end{pmatrix} \) and \( \vec{q} = \begin{pmatrix} 1 \\ 2 \end{pmatrix} \) parallel?
▶️ Answer/Explanation
\( \vec{p} = 4 \cdot \vec{q} \), since \( \vec{p} = \begin{pmatrix} 4 \\ 8 \end{pmatrix} = 4 \cdot \begin{pmatrix} 1 \\ 2 \end{pmatrix} \)
Conclusion: Yes, they are parallel.
Example:
Are the vectors \( \vec{a} = \begin{pmatrix} -3 \\ 6 \end{pmatrix} \) and \( \vec{b} = \begin{pmatrix} 1 \\ -2 \end{pmatrix} \) parallel?
▶️ Answer/Explanation
Try to find a scalar \( k \) such that \( \vec{a} = k \cdot \vec{b} \):
\( \dfrac{-3}{1} = -3 \), \( \dfrac{6}{-2} = -3 \)
Since both components give the same scalar, \( \vec{a} = -3 \cdot \vec{b} \)
Conclusion: Yes, \( \vec{a} \) and \( \vec{b} \) are parallel.
B. Showing 3 Points are Collinear
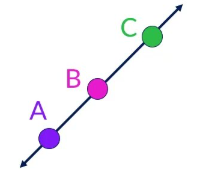
Three points \( A \), \( B \), and \( C \) are collinear if vectors \( \vec{AB} \) and \( \vec{AC} \) are parallel (i.e. one is a scalar multiple of the other).
Example:
Let \( A(1, 2) \), \( B(3, 6) \), and \( C(5, 10) \). Show that points A, B, C are collinear.
▶️ Answer/Explanation
\( \vec{AB} = \begin{pmatrix} 2 \\ 4 \end{pmatrix} \), \( \vec{AC} = \begin{pmatrix} 4 \\ 8 \end{pmatrix} \)
Since \( \vec{AC} = 2 \cdot \vec{AB} \), the points are collinear.
Example:
Let \( A(0, 0) \), \( B(2, 3) \), and \( C(4, 6) \). Show whether they are collinear.
▶️ Answer/Explanation
\( \vec{AB} = \begin{pmatrix} 2 \\ 3 \end{pmatrix}, \quad \vec{AC} = \begin{pmatrix} 4 \\ 6 \end{pmatrix} \)
\( \vec{AC} = 2 \cdot \vec{AB} \), so they are in the same direction.
Conclusion: Points A, B, C are collinear.
C. Vectors and Ratio in Geometry
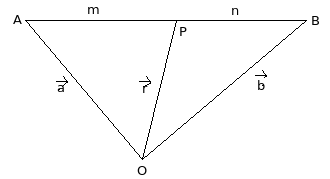
If a point \( P \) lies on line segment \( AB \) and divides it in the ratio \( m:n \), then:
\( \vec{OP} = \vec{OA} + \dfrac{m}{m+n} \vec{AB} \)
Example:
Let \( A = (2, 1) \), \( B = (8, 4) \). Find the position vector of point P that divides AB in the ratio 1:2.
▶️ Answer/Explanation
\( \vec{OA} = \begin{pmatrix} 2 \\ 1 \end{pmatrix}, \quad \vec{AB} = \begin{pmatrix} 6 \\ 3 \end{pmatrix} \)
\( \vec{OP} = \vec{OA} + \dfrac{1}{3} \cdot \vec{AB} = \begin{pmatrix} 2 \\ 1 \end{pmatrix} + \begin{pmatrix} 2 \\ 1 \end{pmatrix} = \begin{pmatrix} 4 \\ 2 \end{pmatrix} \)
Example:
Let \( A = (1, 4) \), \( B = (7, 10) \). Find the coordinates of point P that divides AB in the ratio 2:1.
▶️ Answer/Explanation
\( \vec{OA} = \begin{pmatrix} 1 \\ 4 \end{pmatrix}, \quad \vec{AB} = \begin{pmatrix} 6 \\ 6 \end{pmatrix} \)
\( \vec{OP} = \vec{OA} + \dfrac{2}{3} \cdot \vec{AB} = \begin{pmatrix} 1 \\ 4 \end{pmatrix} + \begin{pmatrix} 4 \\ 4 \end{pmatrix} = \begin{pmatrix} 5 \\ 8 \end{pmatrix} \)
So, coordinates of P: (5, 8)
