Question
A screw gauge has 50 divisions on its circular scale. The circular scale is 4 units ahead of the pitch scale marking,prior to use. Upon one complete rotation of the circular scale, a displacement of 0.5 mm is noticed on the pitch scale. The nature of zero error involved, and the least count of the screw gauge, are respectively:
(a) Negative, 2 μm (b) Positive, 10 μm
(c) Positive, 0.1 mm (d) Positive, 0.1 μm
Answer/Explanation
Ans.
(b)
(b) Given: No. of division on circular scale of screw gauge= 50
Pitch = 0.5 mm
Least count of screw gauge
=\(\frac{Pitch}{No. \; Of \; Division \; on \; circular\; scale}\)
=\(\frac{0.5}{50}mm=1×10^{5}m=10μm\)
Question
A student measuring the diameter of a pencil of circular cross-section with the help of a vernier scale records the following four readings 5.50 mm, 5.55 mm, 5.45 mm, 5.65 mm, The average of these four reading is 5.5375 mm and the standard deviation of the data is 0.07395 mm. The average diameter of the pencil should therefore be recorded as:
(a) (5.5375±0.0739)mm (b) (5.5375±0.0740)mm
(c) (5.538±0.074)mm (d) (5.54±0.07)mm
Answer/Explanation
Ans.
(d)
(d) Average diameter, dav = 5.5375 mm
Deviation of data, \(\Delta d\) = 0.07395 mm
As the measured data are upto two digits after decimal, therefore
answer should be in two digits after decimal.
Question
A physical quantity z depends on four observables a, b, c and d, as z=\(\frac{a^2b^{2/3}}{\sqrt{c}d^3}\). The percentages of error in the measurement of a, b, c and d are 2%, 1.5%, 4% and 2.5% respectively. The percentage of error in z is :
(a) 12.25% (b) 16.5% (c) 13.5% (d) 14.5%
Answer/Explanation
Ans.
(d)
(d) Given: Z =\(\frac{a^2b^{2/3}}{\sqrt{c}d^3}\)
Percentage error in Z,
=\(\frac{\Delta Z}{Z}\)=\(\frac{2\Delta a}{a}+\frac{2}{3}\frac{\Delta b}{b}+\frac{1}{2}\frac{\Delta c}{c}+\frac{3\Delta d}{d}\)
Question
Using screw gauge of pitch 0.1 cm and 50 divisions on its circular scale, the thickness of an object is measured. It should correctly be recorded as:
(a) 2.121cm (b) 2.124cm (c) 2.125cm (d) 2.123cm
Answer/Explanation
Ans.
(a)
(a) Thickness= M.S. Reading+ Circular Scale Reading (L.C.)
Here LC = \(\frac{Pitch}{Circular \; scale \; division}\)=\(\frac{0.1}{50}\)= 0.002 cm per division
So, correct measurement is measurement of integral multiple of L.C
Question
If the screw on a screw-gauge is given six rotations, it moves by 3 mm on the main scale. lf there are 50 divisions on the circular scale the least count of the screw gauge is:
(a) 0.001 cm (b) 0.02 mm (c) 0.01 cm (d) 0.001 mm
Answer/Explanation
Ans.
(a)
(a) When screw on a screw-gauge is given six rotations, it moves by 3mm on the main scale
\(\therefore\) Pitch = \(\frac{3}{6}\) = 0.5mm
\(\therefore\) Least count L.C. =\( \frac{Pitch}{CSD}=\frac{0.5mm}{50}\)
Question
For the four sets of three measured physical quantities as given below. Which of the following options is correct?
(A) A1 = 24.36, B1 = 0.0724, c1 = 256.2
(B) A2 = 24.44, B2 = 16.082, C2 = 240.2
(C) A3= 25.2, B3 = 19.2812, C3 = 236.183
(D) A4 =25,B4 =236.191,C4 =19.5
(a) A4+B4+C4<A1+B1+C1<A3+B3+C3<A2+B2+C2
(b) A1+B1+C1=A2+B2+C2=A3+B3+C3=A4+B4+C4
(c) A4+B4+C4<A1+B1+C1=A2+B2+C2=A3+B3+C3
(d) A1+B1+C1<A3+B3+C3<A2+B2+C2<A4+B4+C4
Answer/Explanation
Ans.
(Bonus)
(Bonus)
D1 = A1 + B1 + C1 = 24.36 + 0.0724 + 256.2 = 280.6
D2 = A2 + B2 + C2 = 24.44 + 16.082 + 240.2 = 280.7
D3 =A3 + B3 + C3 = 25.2 + 19.2812 + 236.183= 280.7
D4 = A4 + B4 + C4 = 25 + 236.191 + 19.5 = 281
Question
A simple pendulum is being used to determine the value of gravitational acceleration g at a certain place. The length of the pendulum is 25.0 cm and a stop watch with 1 s resolution measures the time taken for 40 oscillations to be 50 s. The accuracy in g is:
(a) 5.40% (b) 3.40% (c) 4.40% (d) 2.40%
Answer/Explanation
Ans.
(c)
(c) Given, Length of simple pendulum, l = 25.0 cm
Time of 40 oscillation, T = 50s
Time period of pendulum
T = \(2\pi\sqrt{\frac{l}{g}}\)
⇒ T2 = \(\frac{4\pi ^{2}l}{g}\) ⇒ g = \(\frac{4\pi ^{2}l}{T^{2}}\)
⇒ Fractional error in g = \(\frac{\Delta g}{g}\) = \(\frac{\Delta l}{l}+\frac{2\Delta T}{T}\)
⇒ \(\frac{\Delta g}{g}\) = \(\left ( \frac{0.1}{25.0} \right )+ 2\left ( \frac{1}{50} \right )\) = 0.044
Question
In the density measurement of a cube, the mass and edge length are measured as (10.00 ± 0.10) kg and (0.10 ±0.01) m, respectively. The error in the measurement of density is:
(a) 0.01 kg/m3 (b) 0.10 kg/m3
(c) 0.013 kg/m3 (d) 0.07 kg/m3
Answer/Explanation
Ans.
(Bonus)
(Bonus) δ = \(\frac{M}{V}\) = \(\frac{M}{l^{3}}\) = \(Ml^{-3}\)
Question
The area of a square is 5.29 cm2 . The area of 7 such squares taking into account the significant figures is:
(a) 37 cm2 (b) 37.030 cm2
(c) 37.03 cm2 (d) 37.0 cm2
Answer/Explanation
Ans.
(d)
(d) A= 7 x 5.29 = 37.03 cm2
The result should have three significant figures, so
A=37.0cm
Question
In a simple pendulum experiment for determination of acceleration due to gravity (g), time taken for 20 oscillations is measured by using a watch of 1 second least count. The mean value of time taken comes out to be
30 s. The length of pendulum is measured by using a meter scale of least count 1 mm and the value obtained is 55.0 cm. The percentage error in the determination of g is close to :
(a) 0.7% (b) 0.2% (c) 3.5% (d) 6.8%
Answer/Explanation
Ans.
(d)
(d) We have
T = \(2\pi \sqrt{\frac{l}{g}}\) or g = \(4\pi ^{2}\frac{l}{T^{2}}\)
\(\frac{\Delta g}{g}\)x100 = \(\frac{\Delta R}{Q}\)x100+2\(\frac{\Delta T}{T}\)x100
= \(\frac{0.1}{55}\)x100+2\(\left ( \frac{1}{30} \right )\)x100
Question
The least count of the main scale of a screw gauge is 1 mm. The minimum number of divisions on its circular scale required to measure 5 μm diameter of a wire is:
(a) 50 (b) 200 (c) 100 (d) 500
Answer/Explanation
Ans.
(b)
(b) Least count of main scale of screw gauge = 1 mm
Least count of screw gauge
= \(\frac{Pitch}{Number \; of \; division \; on \; circular \; scale}\)
5×10-6=\(\frac{10^{-3}}{N}\)
Question
The pitch and the number of divisions, on the circular scale for a given screw gauge are 0.5 mm and 100 respectively. When the screw gauge is fully tightened without any object, the zero of its circular scale lies 3 division below the mean line. The readings of the main scale and the circular scale, for a thin sheet, are 5.5 mm and 48 respectively, the thickness of the sheet is:
(a) 5.755mm (b) 5.950mm
(c) 5.725mm (d) 5.740mm
Answer/Explanation
Ans.
(c)
(c) Least count of screw gauge,
LC = \(\frac{Pitch}{No \; of \; division}\)
= 0.5 x 10-3 = 0.5 x 10-2 mm+ ve error= 3 x 0.5 x 10-2 mm
= 1.5 x 10-2mm= 0.015 mm
Reading= MSR + CSR- (+ve error)
= 5.5 mm+ (48 x 0.5 x 10-2)- 0.015
Question
The density of a material in the shape of a cube is determined by measuring three sides of the cube and its mass. If the relative errors in measuring the mass and length are respectively 1.5% and 1 %, the maximum error in determining the density is:
(a) 2.5% (b) 3.5% (c) 4.5% (d) 6%
Answer/Explanation
Ans.
(c)
Question
The percentage errors in quantities P, Q, R and S are 0.5%, 1 %, 3% and 1.5% respectively in the measurement of a physical quantity
A = \(\frac{P^{3}Q^{2}}{\sqrt{RS}}\)
The maximum percentage error in the value of A will be
(a) 8.5% (b) 6.0%,
(c) 7.5% (d) 6.5%
Answer/Explanation
Ans.
(d)
( d) Maximum percentage error in A
= 3(% error in P) + 2(% error in Q)
+ \(\frac{1}{2}\) (%error in R) + 1(% error in S)
= 3 x 0.5+2x 1+\(\frac{1}{2}\) 3+1 x 1.5
Question
In a screw gauge, 5 complete rotations of the screw cause it to move a linear distance of0.25 cm. There are 100 circular scale divisions. The thickness of a wire measured by this screw gauge gives a reading of 4 main scale divisions and 30 circular scale divisions. Assuming negligible zero error, the thickness of the wire is:
(a) 0.0430 cm (b) 0.3150 cm
(c) 0.4300 cm (d) 0.2150 cm
Answer/Explanation
Ans.
(d)
(d) Least count =\(\frac{Value\;of\;1\;part\;on\;main\;scale}{Number\;of\;parts\;on\;vernier\;scale}\)
= \(\frac{0.25}{5×100}cm\) = 5 x 10-4 cm
Reading= 4 x 0.05 cm+ 30 x 5 x 10-4 cm
Question
The following observations were taken for determining surface tensiton T of water by capillary method: Diameter of capilary, D = 1.25 x 10-2 m rise of water, h = 1.45 x 10-2 m
Using g = 9 .80 m/s2 and the simplified relation
T = \(\frac{rhg}{2}\)x 103 N/m, the possible error in surface tension is closest to :
(a) 2.4% (b) 10% (c) 0.15% (d) 1.5%
Answer/Explanation
Ans.
(d)
(d) Surface tension, \(T\) = \(\frac{rhg}{2}\)x 103
Relative error in surface tension,
\(\frac{\Delta T}{T}=\frac{\Delta r}{r}+\frac{\Delta h}{h}+0\) (\(\because \)g, 2 & 103 are constant)
Percentage error
100x \(\frac{\Delta T}{T}\) = \(\left ( \frac{10^{-2}x0.01}{1.25×10^{-2}}+\frac{10^{-2}x0.01}{1.45×10^{-2}} \right )\) 100
= (0.8 + 0.689)
Question
A physical quantity P is described by the relation P = a1/2 b2 c3 d -4 . If the relative errors in the measurement of a, b, c and d respectively, are 2%, 1 %, 3% and 5%, then the relative error in P will be :
(a) 8% (b) 12% (c) 32% (d) 25%
Answer/Explanation
Ans.
(c)
(c) Given, P = a1/2 b2 c2 d-4,
Maximum relative error,
\(\frac{\Delta P}{P}\) = \(\frac{1}{2}\frac{\Delta a}{a}+2\frac{\Delta b}{b}+3\frac{\Delta c}{c}+4\frac{\Delta d}{d}\)
Question
A person measures the depth of a well by measuring the time interval between dropping a stone and receiving the sound of impact with the bottom of the well. The error in his measurement of time is BT= 0.01 seconds and he measures the depth of the well to be L = 20 meters. Take the acceleration due to gravity g = 10 ms-2 and the velocity of sound is 300 ms-1. Then the fractional error in the measurement, BL/L, is closest to
(a) 0.2% (b) 1 % (c) 3% (d) 5%
Answer/Explanation
Ans.
(b)
(b) Depth of the well = L = 20 m
\(\therefore\) Time taken by stone to reach the bottom of well,
t1 = \(\sqrt{\frac{2L}{g}}\) \(\left ( using,L = \frac{1}{2}gt^{2} \right )\)
Time taken by impact sound to reach the person,
t2 = \(\frac{L}{V}\)
Total time taken in the process is given by,
T = t1 + t2 = \(\sqrt{\frac{2L}{g}}+\frac{L}{V}\)
\(\therefore\) \(\delta\)T = \(\sqrt{\frac{2}{g}}\frac{1}{2}\frac{\delta L}{\sqrt{L}}+\frac{\delta L}{v}\)
On substituting the given values we get,
\(\delta\)T = \(\frac{16}{300}\delta L\)
\(\therefore\) Fractional error, \(\frac{\delta L}{L}\)x100 = \(\frac{300}{16}\frac{\delta T}{L}\)x100
Question
A screw gauge with a pitch of 0.5 mm and a circular scale with 50 divisions is used to measure the thickness of a thin sheet of Aluminium. Before starting the measurement, it is found that wen the two jaws of the screw gauge are brought in contact, the 45th division coincides with the main scale line and the zero of the main scale is barely visible. What is the thickness of the sheet if the main scale reading is 0.5 mm and the 25th division coincides with the main scale line?
(a) 0.70mm (b) 0.50mm
(c) 0.75mm (d) 0.80mm
Answer/Explanation
Ans.
(d)
(d) L.C. = \(\frac{0.5}{50}\) = 0.01 mm
Zero error= 5 x 0.01 = 0.05 mm (Negative)
Question
A student measures the time period of 100 oscillations of a simple pendulum four times. The data set is 90 s, 91 s, 95 s, and 92 s. If the minimum division in the measuring clock is 1 s, then the reported mean time should be:
(a) 92 ± 1.8s (b) 92 ± 3s
(c) 92 ± 1.5s (d) 92 ± 5.0s
Answer/Explanation
Ans.
(c)
(c) \(\Delta T\) = \(\frac{\left | \Delta T_{1} \right |+\left | \Delta T_{2} \right |+\left | \Delta T_{3} \right |+\left | \Delta T_{4} \right |}{4}\)
= \(\frac{2+1+3+0}{4}\) = 1.5
As the resolution of measuring clock is 1.5 therefore the mean
Question
There are two Vernier calipers both of which have 1 cm divided into 10 equal divisions on the main scale. The Vernier scale of one of the calipers (C1) has 10 equal divisions that correspond to 9 main scale divisions. The Vernier scale of the other caliper (C2) has 10 equal divisions that correspond to 11 main scale divisions. The readings of the two calipers are shown in the figure. The measured values (in cm) by calipers C1 and C2, respectively, are
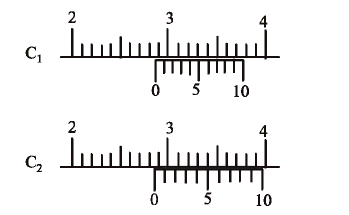
(a) 2.85 and 2.82 (b) 2.87 and 2.83
(c) 2.87 and 2.86 (d) 2.87 and 2.87
Answer/Explanation
Ans.
(b)
(b) For C1 vernier calliper,
L.C. = 1 MSD – 1 VSD = 1mm – 0.9 mm= 0.1 mm= 0.01 cm
[\(\because \) 10 VSD = 9 MSD = 9 mm]
Reading= MSR + L.C. x VSR = 2.8 + (0.01) x 7 = 2.87 cm
For C2 vernier calliper,
L.C. = 1 mm – 1.1 mm [\(\because \) 10 VSD 11 MSD = 11 mm]
L.C=-0.1 mm = -0.01 cm
Question
The period of oscillation of a simple pendulum is T= \(2\pi \sqrt{\frac{L}{g}}\) Measured value of L is 20.0 cm known to 1 mm accuracy and time for 100 oscillations of the pendulum is found to be 90 s using a wrist watch of 1 s resolution. The accuracy in the determination of g is:
(a) 1% (b) 5% (c) 2% (d) 3%
Answer/Explanation
Ans.
(d)
(d) As g = \(4\pi ^{2}\frac{L}{T^{2}}\)
So, \(\frac{\Delta g}{g}\)x 100 = \(\frac{\Delta L}{L}\)x 100 + 2\(\frac{\Delta T}{T}\)x 100
Question
Diameter of a steel ball is measured using a Vernier callipers which has divisions of 0.1 cm on its main scale (MS) and 10 divisions of its vernier scale (VS) match 9 divisions on the main scale. Three such measurements for a ball are given as :
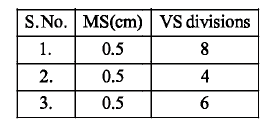
If the zero error is- 0.03 cm, then mean corrected diameter
is:
(a) 0.52 cm (b) 0.59 cm
(c) 0.56 cm (d) 0.53 cm
Answer/Explanation
Ans.
(b)
(b) Least count = \(\frac{0.1}{10}\) = 0.01 cm
d1 = 0.5 + 8 x 0.01 + 0.03 = 0.61 cm
d2 = 0.5 + 4 x 0.01 + 0.03 = 0.57 cm
d3 = 0.5 + 6 x 0.01 + 0.03 = 0.59 cm
Question
The current voltage relation of a diode is given by I = \(\left (e ^{1000V/T}-1 \right )\)mA, where the applied voltage V is in volts and the temperature T is in degree kelvin. If a student makes an error measuring ±0.01 V while measuring the current of 5 mA at 300K, what will be the error in the value of current in mA?
(a) 0.2 mA (b) 0.02 mA (c) 0.5 mA (d) 0.05 mA
Answer/Explanation
Ans.
(a)
(a) The current voltage relation of diode is
\(I\) = \(\left (e ^{1000V/T}-1 \right )\) mA (given)
When,\(I\) = 5mA, \(e^{1000 V/T}\) = 6mA
Also, d\(l\) = \(\left (e ^{1000V/T} \right )\) x \(\frac{1000}{T}\)
Error=± 0.01 (By exponential function)
Question
A student measured the length of a rod and wrote it as 3 .50 cm. Which instrument did he use to measure it?
(a) A meter scale.
(b) A vernier calliper where the 10 divisions in vernier
scale matches with 9 division in main scale and main
scale has 10 divisions in 1 cm.
(c) A screw gauge having 100 divisions in the circular
scale and pitch as 1 mm.
( d) A screw gauge having 50 divisions in the circular scale
and pitch as 1 mm.
Answer/Explanation
Ans.
(b)
(b) Measured length of rod= 3.50 cm
For Vernier Scale with 1 Main Scale Division= 1 mm
9 Main Scale Division = 10 Vernier Scale Division,
Question
In the experiment of calibration of voltmeter, a standard cell of e.m.f 1.1 volt is balanced against 440 cm of potential wire. The potential difference across the ends of resistance is found to balance against 220 cm of the wire. The corresponding reading of voltmeter is 0.5 volt. The error in the reading of voltmeter will be:
(a) -0.15 volt (b) 0.15 volt
(c) 0.5 volt (d) -0.05 volt
Answer/Explanation
Ans.
(d)
(d) In a voltmeter
V ![]() \(l\)
\(l\)
V=k\(l\)
Now, it is given E = 1.1 volt for \(l_{1}\) = 440 cm
and V = 0.5 volt for \(l_{1}\) = 220 cm
Let the error in reading of voltmeter be \(\Delta V\) then,
1.1 = 400 K and (0.5 – \(\Delta V\)) =220 K.
⇒\(\frac{1.1}{440}=\frac{0.5-\Delta V}{220}\)
Question
An experiment is performed to obtain the value of acceleration due to gravity g by using a simple pendulum of length L. In this experiment time for 100 oscillations is measured by using a watch of 1 second least count and the value is 90.0 seconds. The length Lis measured by using a meter scale ofleast count 1 mm and the value is 20.0 cm. The error in the determination of g would be:
(a) 1.7% (b) 2.7% (c) 4.4% (d) 227%
Answer/Explanation
Ans.
(b)
(b) According to the question.
\(t=(90\pm 1)\) or, \(\frac{\Delta t}{t}=\frac{1}{90}\)
\(l=(20\pm 0.1)\) or, \(\frac{\Delta l}{l}=\frac{0.1}{20}\)
\(\frac{\Delta g}{g}\)% = ?
As we know,
\(t=2\pi \sqrt{\frac{l}{g}}\Rightarrow g=\frac{4\pi ^{2}l}{t^{2}}\)
or, \(\frac{\Delta g}{g}=\pm \left ( \frac{\Delta l}{l}+2\frac{\Delta t}{t} \right )=\left ( \frac{0.1}{20}+2x\frac{1}{90} \right ) \)=0.027
Question
The diameter of a cylinder is measured using a Vernier callipers with no zero error. It is found that the zero of the Vernier scale lies between 5.10 cm and 5.15 cm of the main scale. The Vernier scale has 50 divisions equivalent to 2.45 cm. The 24th division of the Vernier scale exactly coincides with one of the main scale divisions. The diameter of the cylinder is
(a) 5.112 cm (b) 5.124 cm
(c) 5.136 cm (d) 5.148 cm
Answer/Explanation
Ans.
(b)
(b) In the measurement, the diameter of cylinder,
D = M.S.R + (V.S.R) x (L.C.) L.C. = (1 MSD – 1 VSD)
= (5.15-5.10)-\(\left ( \frac{2.45}{50} \right )\)= .001 cm
Question
In the determination of Young’s modulus \(\left ( Y=\frac{4MLg}{\pi ld^{2}} \right )\)
by using Searle’s method, a wire of length \(L\) = 2 m and diameter \(d\) = 0.5 mm is used. For a load \(M\) = 2.5 kg, an extension \(l\)= 0.25 mm in the length of the wire is observed. Quantities \(d\) and \(l\) are measured using a screw gauge and a micrometer, respectively. They have the same pitch of 0.5 mm. The number of divisions on their circular scale is 100. The contributions to the maximum probable error of the \(Y\) measurement
(a) due to the errors in the measurements of \(d\)
and \(l\) are the same.
(b) due to the error in the measurement of \(d\) is twice that
due to the error in the measurement of \(l\).
( c) due to the error in the measurement of \(l\) is twice that
due to the error in the measurement of \(d\).
( d) due to the error in the measurement of \(d\) is four times
that due to the error in the measurement of \(l\).
Answer/Explanation
Ans.
(a)
(a) The maximum possible error in \(Y\) due to \(l\) and \(d\)
\(\frac{\Delta Y}{Y}=\frac{\Delta l}{l}+\frac{2\Delta d}{d}\)
Least count = \(\frac{Pitch}{No.\;of\;division\;on\;circular\;scale}\)
= \(\frac{0.5}{100}mm = 0.005 mm\)
Here, \(\Delta d=\Delta l= 0.005 mm\)
Error contribution of \(l\) = \(\frac{\Delta l}{l}=\frac{0.005 mm}{0.25 mm}=\frac{1}{50}\)
Error contribution of \(d\) =\(\frac{2\Delta d}{d}=\frac{2×0.005 mm}{0.5 mm}=\frac{1}{50}\)
Hence contribution to the maximum possible error in the
Question
The density of a solid ball is to be determined in an experiment. The diameter of the ball is measured with a screw gauge, whose pitch is 0.5 mm and there are 50 divisions on the circular scale. The reading on the main scale is 2.5 mm and that on the circular scale is 20 divisions. If the measured mass of the ball has a relative error of 2 %, the relative percentage error in the density is
(a) 0.9% (b) 2.4% (c) 3.1 % (d) 4.2%
Answer/Explanatio
Ans.
(c)
(c) Least count of screw gauge
= \(\frac{Pitch}{divisions\;on\;circular\;scale}=\frac{0.5}{50}=0.01mm = \Delta r\)
Diameter, \(r\) = M.S.R. + (C.S.R) x (L.C.)
Diameter, \(r\) = 2.5 mm+ 20 x \(\frac{0.5}{50}\) = 2.70 mm
\(\frac{\Delta r}{r}=\frac{0.01}{2.70}or\frac{\Delta r}{r}\)x 100 = \(\frac{1}{2.7}\)
Now, density, \(d=\frac{m}{V}=\frac{m}{\frac{4}{3}\pi \left ( \frac{r}{2} \right )^{3}}\)
∴ Percentage error in density, \(\frac{\Delta d}{d}\)x100
= \(\left \{ \frac{\Delta m}{m}+3\left ( \frac{\Delta r}{r} \right ) \right \}\)x100
=\(\frac{\Delta m}{m}\)x100+3x\(\left ( \frac{\Delta r}{r} \right )\)x100
= 2% + 3 x \(\frac{1}{2.7}\) = 3.11%
Question
A vernier calipers has 1 mm marks on the main scale. It has 20 equal divisions on the Vernier scale which match with 16 main scale divisions. For this Vernier calipers, the least count is
(a) 0.02 mm (b) 0.05 mm (c) 0.1 mm (d) 0.8 mm
Answer/Explanation
Ans.
(d)
(d) 20 divisions on the vernier scale
= 16 divisions of main scale
∴ 1 division on the vernier scale
= \(\frac{16}{20}\) divisions of main scale = \(\frac{16}{20}\)x 1 mm = 0.8 mm
Question
Students I, II and III perform an experiment for measuring the acceleration due to gravity \((g)\) using a simple pendulum. They use different lengths of the pendulum and /or record time for different number of oscillations. The observations are shown in the table.
Least count for length= 0.1 cm
Least count for time= 0.1 s
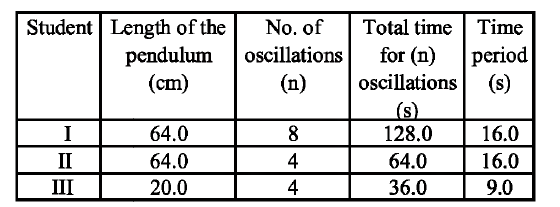
If \(E_{I}\), \(E_{II}\) and \(E_{III}\) are the percentage errors in\(g\), i.e.,
\(\left ( \frac{\Delta g}{g}x100 \right )\) for students I, II and III, respectively, then
(a) \(E_{I}\)=0 (b) \(E_{I}\) is minimum
(c) \(E_{I}\)=\(E_{II}\) (d) \(E_{II}\) is maximum
Answer/Explanation
Ans.
(b)
(b) The time period of a simple pendulum is given by
\(T=2\pi \sqrt{\frac{l}{g}}\Rightarrow T^{2}=4\pi ^{2}\frac{l}{g}\Rightarrow g=4\pi ^{2}\frac{l}{T^{2}}\)
Percentage error in \(g\) = \(\frac{\Delta g}{g}\)x100
=\(\frac{\Delta l}{l}\)x100+2\(\frac{\Delta T}{T}\)x100
Putting the values of \(\Delta l\),\(l\),\(\Delta T\) and \(T\) we get E1 = 0.3125%
least among E1, E2 and E3.
Question
A student performs an experiment to determine the Young’s modulus of a wire, exactly 2 m long, by Searle’s method. In a particular reading, the student measures the extension in the length of the wire to be 0.8 mm with an uncertainty of± 0.05 mm at a load of exactly 1.0 kg. The student also measures the diameter of the wire to be 0.4 mm with an uncertainty of± 0.01 mm. Takeg= 9.8 m/s2 (exact). The Young’s modulus obtained from the reading is
(a) (2.0 ± 0.3) x 1011 N/m2 (b) (2.0 ± 0.2) x 1011 N/m2
(c) (2.0 ±0.1) x 1011 N/m2 (d) (2.0±0.05) x 1011 N/m2
Answer/Explanation
Ans.
(b)
(b) \(Y = \frac{F/A}{l/L}=\frac{4mgL}{\pi D^{2}l}=\frac{4x1x9.8×2}{\pi \left ( 0.4×10^{-3}\right )^{2}x\left (0.8×10^{-3} \right )}\)
= 2.0 x 1011 N/m2
Now \(\frac{\Delta Y}{Y}=\frac{2\Delta D}{D}+\frac{\Delta l}{l}\)
[\(\because\) the value of \(m\), \(g\) and \(L\) are exact]
= 2 x \(\frac{0.01}{0.4}+\frac{0.05}{0.8}\) 2 x 0.025 + 0.0625
= 0.05 + 0.0625 = 0.1125
⇒ \(\Delta Y\) = \(Y\) x 0.1125 = 2 x 1011 x 0.1125 = 0.225 x 1011
= 0.2 x 1011 N/m2
∴ Reading of Young’s modulus= (\(Y\) + \(\Delta Y\))
= (2±0.2)x 1011 N/m
Question
A student performs an experiment for determination of \(g\left ( =\frac{4\pi ^{2}l}{T^{2}} \right )\). The error in length \(\ l\) is \(\Delta l\) and in time \(T\) is \(\Delta T\)
and \(n\) is number of times the reading is taken. The measurement of g is most accurate for

Answer/Explanation
Ans.
(d)
( d) Relative error in \(g\), \(\frac{\Delta g}{g}=\frac{\Delta l}{l}+2\frac{\Delta T}{T}\)
\(\Delta l\) and \(\Delta T\) are least and number of readings taken are maximum
Question
In a screw gauge, the zero of mainscale coincides with fifth division of circular scale in figure (i). The circular division of screw gauge are 50. It moves 0.5 mm on main scale in one rotation. The diameter of the ball in figure (ii) is
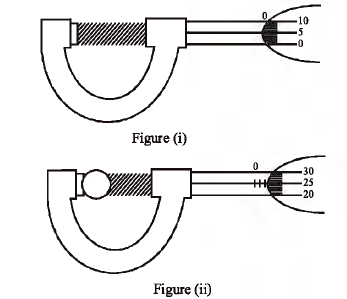
(a) 2.25 mm (b) 2.20 mm
(c) 1.20 mm (d) 1.25 mm
Answer/Explanation
Ans.
(c)
(c) Least count = \(\frac{Pitch}{no.\;of\;divisions\;on\;circular\;scale}\)
= \(\frac{0.5}{50}\)= 0.01 mm
Zero error= 5 x L.C. = 5 x 0.01 mm= 0.05 mm
Diameter of ball = [Reading on main scale] + [Reading on circular
scale x L.C.] – Zero error
Question
A wire of length \(\ l\) = 6±0.06 cmandradius \(r\)=0.5 ±0.005 cm and mass \(m\) = 0.3 ± 0.003 gm. Maximum percentage erroc in density is
(a) 4 (b) 2 (c) 1 (d) 6.8
Answer/Explanation
Ans.
(a)
(a) Density, \(\rho = \frac{m}{v}=\frac{m}{Al}=\frac{m}{l\pi r^{2}}\)
Taking log and differentiate for errors
\(\frac{\Delta \rho }{\rho }=\frac{\Delta m}{m}+\frac{2\Delta r}{r}+\frac{\Delta l}{l}\) ….(i)
From question, putting the values of
\(\Delta l\) = 0.06 cm, \(l\) = 6 cm; \(\Delta r\)= 0.005 cm; \(r\) = 0.5 cm,
\(m\) = 0.3 g; \(\Delta m\)= 0.003 g in eqn. (i) we get
\(\frac{\Delta \rho }{\rho }\)=\(\frac{4 }{100 }\)
∴ Percentage error in density,
Question
A cube has a side of length 1.2 x 10-2m. Calculate its volume.
(a) 1.7 x 10-6m3 (b) 1.73 x 10-6m3
(c) 1.70 x 10-6m3 (d) 1.732 x 10-6m3
Answer/Explanation
Ans.
(a)
(a) Volume of cube, \(V\)= \(l\)3= (1.2 x 10-2 m)3
= 1.728 X 10-6 m3
⇒ \(V\) = 1.7 x 10-6 m3
As length has two significant figures so volume has also
Question
The energy of a system as a function of time t is given as \(E(t)\) = \(A\)2 exp(-αt,) where α= 0.2 s-1• The measurement of \(A\) has an error of 1.25%. If the error in the measurement of time is 1.50%, the percentage error in the value of \(E(t)\) at \(t\) = 5 s is
Answer/Explanation
Ans.
(4) \(E_{t}=A^{2}e^{-\alpha t}=A^{2}e^{-0.2t}\)
∴ loge \(E\) = 2 loge \(A -0 .2t\)
On differentiating we get
\(\frac{dE}{E}=2\frac{dA}{A}-0.2\frac{dt}{t}\)x t
As errors always add up
∴ \(\frac{dE}{E}\)x 100 = 2 \(\left ( \frac{dA}{A}x100 \right )+0.2t\left ( \frac{dt}{t} x100\right )\)
Question
During Searle’s experiment, zero of the Vernier scale lies between 3.20 x 10-2 mand3.25 x 10-2 m of the mainscale. The 20th division of the Vernier scale exactly coincides with one of the main scale divisions. When an additional load of 2 kg is applied to the wire, the zero of the Vernier scale still lies between 3.20 x 10-2 m and 3.25 x 10-2 m of the main scale but now the 45th division of Vernier scale coincides with one of the main scale divisions. The length of the thin metallic wire is 2 m and its cross-sectional area is 8 x 10-7 m2. The least count of the Vernier scale is 1.0 x 10-5 m. The maximum percentage error in the Young’s modulus of the wire is
Answer/Explanation
Ans.
(4)
(4) Young’s modulus \(Y=\frac{FL}{Axl}\)
Here F, A and L are accurately known.
∴ Percentage error in Young’s modulus
Question
The density of a solid metal sphere is determined by measuring its mass and its diameter. The maximum error in the density of the sphere is
\(\left ( \frac{x}{100} \right )\)%. If the relative errors in measuring the mass and the diameter are 6.0% and 1.5% respectively, the value of x is ___ .
Answer/Explanation
Ans.
(1050)
(1050)
Density, \(\rho = \frac{M}{V}=\frac{M}{\frac{4}{3}\pi \left ( \frac{D}{2} \right )^{3}}\Rightarrow \rho =\frac{6}{\pi }MD^{-3}\)
∴ % \(\left ( \frac{\Delta \rho }{\rho } \right )=\frac{\Delta m}{m}+3\left ( \frac{\Delta D}{D} \right ) \) = 6+3 x 1.5 = 10.5%
%\(\left ( \frac{\Delta \rho }{\rho } \right )= \frac{1050}{100}\)%=\(\left ( \frac{x}{100} \right )\)%
Question
Two capacitors with capacitance values C1 = 2000 ± 10 pF and C2 = 3000 ± 15 pF are connected in series. The voltage applied across this combination is V = 5.00 ± 0.02 V. The percentage error in the calculation of the energy stored in this combination of capacitors is ___ .
Answer/Explanation
Ans.
(1.30)
(1.30)
Two capacitors, C1 and C2 are connected in series
∴ \(\frac{1}{C_{eq}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\Rightarrow C_{eq}=\frac{C_{1}C_{2}}{C_{1}+C_{2}}\)
\(C_{eq}=\frac{2000×3000}{5000}=\frac{6000}{5}pF\)
\(\frac{1}{C_{eq}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}\Rightarrow -\frac{\Delta C}{C_{eq}^{2}}=-\frac{\Delta C_{1}}{C_{1}^{2}}-\frac{\Delta C_{2}}{C_{2}^{2}}\)
\(\Rightarrow \Delta C=C_{eq}^{2}\left [ \frac{\Delta C_{1}}{C_{1}^{2}} +\frac{\Delta C_{2}}{C_{2}^{2}}\right ]\)
\(\Rightarrow \Delta C=\frac{6000}{5}x\frac{6000}{5}\left [ \frac{10}{2000×2000}+\frac{15}{3000×3000} \right ]\)
=10 x \(\frac{9}{25}\) + 15 x \(\frac{4}{25}\) = 6pF
Energy stored in a capacitor,
U = \(\frac{1}{2}CV^{2}\Rightarrow \frac{\Delta U}{U}x100=\frac{\Delta C}{C_{eq}}x100+2\frac{\Delta V}{V}x100\)
\(\Rightarrow \frac{\Delta U}{U}x100=\frac{6×5}{6000}x100+2x\frac{0.02}{5}x100\)
Question
An optical bench has 1.5 m long scale having four equal divisions in each cm. While measuring the focal length of a convex lens, the lens is kept at 75 cm mark of the scale and the object pin is kept at 45 cm mark. The image of the object pin on the other side of the lens overlaps with image pin that is kept at 135 cm mark. In this experiment, the percentage error in the measurement of the focal length of the lens is____.
Answer/Explanation
Ans.
(1.39)
(1.39)
\(u\pm \Delta u\)=\((75-45)\pm \left ( \frac{1}{4}+\frac{1}{4} \right )=(30\pm 0.5)cm\)
\(v\pm \Delta v\)=\((135-75)\pm \left ( \frac{1}{4}+\frac{1}{4}\right )=(60\pm 0.5)cm\)
We know that
\(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\)
∴ \(+\frac{\Delta v}{v^{2}}+\frac{\Delta u}{u^{2}}=\frac{\Delta f}{f^{2}}\) …. (i)
Now \(\frac{1}{v}-\frac{1}{u}=\frac{1}{f}\Rightarrow \frac{1}{60}-\frac{1}{-30}=\frac{1}{f}\)
\(\Rightarrow \frac{1}{f}=\frac{1}{20}\) ∴ f = 20 cm
Substituting the values in eqn. (i)
\(\frac{0.5}{\left ( 60 \right )^{2}}+\frac{0.5}{\left ( 30 \right )^{2}}=\frac{\Delta f}{\left ( 20 \right )^{2}}\)
∴ \(\Delta f\) = 0.277
Hence percentage error in the measurement of focal length
Question
A steel wire of diameter 0.5 mm and Young’s modulus 2 x 1011 N m-2 carries a load of mass \(M\). The length of the wire with the load is 1.0 m. A vernier scale with 10 divisions is attached to the end of this wire. Next to the steel wire is a reference wire to which a main scale, of least count 1.0 mm, is attached. The 10 divisions of the vernier scale correspond to 9 divisions of the main scale. Initially, the zero of vernier scale coincides with the zero of main scale. If the load on the steel wire is increased by 1.2 kg, the vernier scale division which coincides with a main scale division is ____ . Take g= 10ms-2 and \(\pi \)=3.2.
Answer/Explanation
Ans.
(3.00)
(3.00) We know that \(\Delta l=\frac{Fl}{AY}\)
= \(\frac{1.2x10x1}{\pi \left ( \frac{5×10^{-4}}{2} \right )^{2}x2x10^{11}}\simeq 0.3mm\)
L.C. of vernier calliper= 1 MSD – 1 VSD
= \(\left ( 1-\frac{9}{10} \right )\)= 0.1 mm
As 9 MSD = 10 VSD
The third marking of vernier scale will coincide with the main
Question
The side of a cube is measured by vernier callipers (10 divisions of a vernier scale coincide with 9 divisions of main scale, where 1 division of main scale is 1 mm). The main scale reads 10 mm and first division of vernier scale coincides with the main scale. Mass of the cube is 2. 736 g. Find the density of the cube in appropriate significant figures.
Answer/Explanation
Ans.
(2.66 g cm-3)
(2.66 g cm-3)
L.C. = 1 MSD-1 VSD
= \(1 MSD-\frac{9}{10}MSD\) (\(\because \) 9 MSD = 10 VSD)
= \(\left ( 1-\frac{9}{10} \right )MSD=\frac{1}{10}MSD=\left (\frac{1}{10}x1 \right )mm=0.1 mm\)
(\(\because \) 1 MSD= 1 mm)
Reading of side,\(l\)= MSR + VSR (LC)= 10 mm + 1 x 0.1 mm
= 10.1 mm= 1.01 cm
Now, density = \(\frac{mass}{volume}=\frac{m}{l^{3}}=\frac{2.736g}{\left ( 1.01 \right )^{3}}= 2.66 g/cm^{3}\)
Question
In Searle’s experiment, which is used to find Young’s Modulus of elasticity, the diameter of experimental wire is D = 0.05 cm (measured by a scale of least count 0.001 cm) and length is L = 110 cm (measured by a scale of least count 0.1 cm). A weight of 50 N causes an extension of X = 0.125 cm (measured by a micrometer of least count 0.001 cm). Find maximum possible error in the values of Young’s modulus. Screw gauge and meter scale are free from error.
Answer/Explanation
Ans.
(1.09 x 1010N/m2)
(1.09 x 1010N/m2)
Young’s modulus, \(Y=\frac{F}{A}/\frac{X}{L}=\frac{F}{\frac{\pi D^{2}}{4}}x\frac{L}{X}\)
Maximum error in Y
\(\left ( \frac{\Delta Y}{Y} \right )_{max}=2\left ( \frac{\Delta D}{D} \right )+\frac{\Delta X}{X}+\frac{\Delta L}{L}\)
\(2\left ( \frac{0.001}{0.05} \right )+\left ( \frac{0.001}{0.125} \right )+\left ( \frac{0.1}{110} \right )= 0.0489\)
Since, W= 50 N; D = 0.05 cm= 0.05 x 10-2m;
X = 0.125 cm= 0.125 x 10-2m;
L = 110 cm= 110 x 10-2m
∴ \(Y=\frac{50x4x110x10^{-2}}{3.14(0.05×10^{-2})x(0.125×10^{-2})}=2.24 x 10^{11}N/m^{2}\)
∴ Maximum possible error in the measurement of Y
\(\Delta Y\) = (0.0489)Y = 0.0489 x 2.24 x 1011
= 1.09 x 1010 N/m
Question
A screw gauge having 100 equal divisions and a pitch of length 1 mm is used to measure the diameter of a wire of length 5.6 cm. The main scale reading is 1 mm and 47th circular division coincides with the main scale. Find the curved surface area of wire in cm2 to appropriate significant figure.
(use\(\pi =\frac{22}{7}\)).
6 MCQs with One or More than One Correct Answer
Answer/Explanation
Ans.
(2.6cm2)
(2.6cm2)
Least count, L.C. = \(\frac{1mm}{100}=0.01mm\)
Diameter = MSR + CSR x (L.C.)
= 1 mm+ 47 x (0.01) mm= 1.47 mm
Curved surface area = \(2\pi rl=2\pi \frac{D}{2}l=\pi Dl\)
= \(\frac{22}{7}\) x 1.47 x 56 mm2 = 2.58724 cm2
= 2.6 cm2
Question
In an experiment to determine the acceleration due to gravity g, the formula used for the time period of a periodic motion is T = \(2\pi \sqrt{\frac{7(R-r))}{5g}}\). The values of R and r are measured to be ( 60 ± 1) mm and (10 ± 1) mm, respectively. In five successive measurements, the time period is found to be 0.52s, 0.56s, 0.57s, 0.54s and 0.59s. The least count of the watch used for the measurement of time period is 0.01s.
Which of the following statement( s) is (are) true?
(a) The error in the measurement of r is 10%
(b) The error in the measurement of T is 3. 75%
( c) The error in the measurement of T is 2%
( d) The error in the determined value of g is 11 %
Answer/Explanation
Ans.
(a, b, d)
(a, b, d)
\(T_{mean}=\frac{0.52+0.56+0.57+0.54+0.59}{6}=0.556\approx 0.56 S\)
Error in reading Tmean-T1; Tmean-T2; Tmean-T3; Tmean-T4;Tmean -T5
Mean error = \(\frac{0.04+0+0.01+0.02+0.03}{6}=0.016\approx 0.02S\)
∴ % error in the measurement of ‘T’
\(\frac{\Delta T}{T}x100=\frac{0.02}{0.56}x100=3.57%\)
% error in the measurement of g
\(\frac{\Delta g}{g}x100=2\frac{\Delta T}{T}x100+\left ( \frac{\Delta R+\Delta r}{R-r} \right )x100\)
= \(2(3.57)+\left ( \frac{1+1}{60-10} \right )x100\approx 11%\)
% error in the measurement of r
Question
Consider a Vernier callipers in which each 1 cm on the main scale is divided into 8 equal divisions and a screw gauge with 100 divisions on its circular scale. In the Vernier callipers, 5 divisions of the Vernier scale coincide with 4 divisions on the main scale and in the screw gauge, one complete rotation of the circular scale moves it by two divisions on the linear scale. Then :
(a) If the pitch of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gaugeis 0.01 mm
(b) If the pitch of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.005 mm
(c) If the least count of the linear scale of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.01 mm
( d) If the least count of the linear scale of the screw gauge is twice the least count of the Vernier callipers, the least count of the screw gauge is 0.005 mm
Answer/Explanation
Ans.
(b,c)
(b, c)
Vernier callipers
1 MSD = \(\frac{1cm}{8}\) = 0.125 cm
5 VSD=4 MSD
∴ 1 VSD = \(\frac{4}{5}\)x 0.125 = 0.1 cm
L.C. = 1 MSD – 1 VSD
= 0.125 cm-0.1 cm = 0.025cm
Screw gauge
If the pitch of screw gauge is twice the L.C of vernier callipers
then pitch = 2 x L.C. of vernier calliper = 2 x 0.025 = 0.05cm.
L.C. of screw gauge
= \(\frac{Pitch}{Total\;no.\;of\;divisions\;of\;circular\;scale}\)
= \(\frac{0.05}{100}cm\) = 0.0005cm = 0 .005 mm.
Now if the least count of the linear scale of the screw gauge is
twice the least count of venier callipers then
L.C. of linear scale of screw gauge= 2 x 0.025 = 0.05 cm.
Then pitch= 2 x 0.05 = 0.1 cm.
Question
Using the expression 2d sin θ=λ, one calculates the values of d by measuring the corresponding angles θ in the range 0 to 90°. The wavelength λ is exactly known and the error in θ is constant for all values of θ. As θ increases from 0°
(a) The absolute error in \(d\) remains constant
(b) The absolute error in \(d\) increases
( c) The fractional error in \(d\) remains constant
( d) The fractional error in \(d\) decreases
Answer/Explanation
Ans.
(d)
(d) \(\because \) 2d sin θ = λ ∴ d = \(\frac{\lambda }{2}cosec\theta \) … (i)
∴ \(\frac{d(d)}{d\theta }=\frac{\lambda }{2}[-cosec\theta cot\theta ]\)
∴ d( d) = \(\frac{\lambda }{2}\) cosecθ cotθ dθ … (ii)
Dividing (ii) by (i) we get
\(\left |\frac{d(d)}{d} \right |=cot\theta d\theta\)
As θ increases from 0° to 90°, cot θ decreases and therefore
\(\left |\frac{d(d)}{d} \right |\) decreases
Question
A student uses a simple pendulum of exactly 1 m length to determine g, the acceleration due to gravity. He uses a stop watch with the least count of 1 sec for this and records 40 seconds for 20 oscillations. For this observation, which of the following statement(s) is (are) true?
(a) Error \(\Delta T\) in measuring T, the time period, is 0.05 seconds
(b) Error \(\Delta T\) in measuring T, the time period, is 1 second
( c) Percentage error in the determination of g is 5%
( d) Percentage error in the determination of g is 2.5%
Answer/Explanation
Ans.
(a, c)
(a, c) The length of the string of simple pendulum is exactly 1 m
(given), therefore the error in length \(\Delta l\) = 0.
Further the possibility of error in measuring time is 1 s in 40 s as the least count of stop watch is 1 s.
∴ \(\frac{\Delta t}{t}=\frac{\Delta T}{T}=\frac{1}{40}\)
Trme period T = \(\frac{total\; time}{no.\;of\;oscillations}=\frac{40}{20}\)= 2 seconds
∴ \(\frac{\Delta T}{T}=\frac{1}{40}\Rightarrow \frac{\Delta T}{2}=\frac{1}{40}\Rightarrow \Delta T = 0.05 sec\)
Now for measuring error in ‘g’
using, \(T=2\pi \sqrt{\frac{1}{g}}\Rightarrow T^{2}=4\pi ^{2}\frac{l}{g}\)
∴ \(g=4\pi ^{2}\frac{l}{T^{2}}\)
∴ Percentage error in ‘g’
\(\frac{\Delta g}{g}x100=\frac{\Delta l}{l}x100+2\frac{\Delta T}{T}x100\)
Comprehension/Passage Based Questions
Passage
If the measurement errors in all the independent quantities are known, then it is possible to determine the error in any dependent quantity. This is done by the use of series expansion and truncating the expansion at the first power of the error. For example, consider the relation z = x/y. If the errors in x, y and z are \(\Delta x\), \(\Delta y\) and \(\Delta z\), respectively, then
\(z\pm \Delta z=\frac{x\pm \Delta x}{y\pm \Delta y}=\frac{x}{y}\left ( 1\pm \frac{\Delta x}{x} \right )\left ( 1\pm \frac{\Delta y}{y} \right )^{-1}\)
The series expansion for \(\left ( 1\pm \frac{\Delta y}{y} \right )^{-1}\), to first power in \(\Delta y/y\), is \(1\mp (\Delta y/y)\).
The relative errors in independent variables are always added. So the error in z will be \(\Delta z=z\left ( \frac{\Delta x}{x}+\frac{\Delta y}{y} \right )\).
The above derivation makes the assumption that \(\Delta x/x\ll 1\),\(\Delta y/y\ll 1\). Therefore, the higher powers of these quantities are neglected.
Question
Consider the ratio \(r=\frac{(1-a)}{(1+a)}\) to be determined by measuring a dimensionless quantity \(a\). If the error in the measurement of \(a\) is \(\Delta a(\Delta a/a\ll 1\), then what is the error \(\Delta r\) in determining \(r\)?
(a) \(\frac{\Delta a}{(1+a)^{2}}\) (b) \(\frac{2\Delta a}{(1+a)^{2}}\) (c) \(\frac{2\Delta a}{(1-a)^{2}}\) (d) \(\frac{2a\Delta a}{(1-a)^{2}}\)
Answer/Explanation
Ans.
(b)
(b) \(r=\left ( \frac{1-a}{1+a} \right )\Rightarrow \frac{\Delta r}{r}=\frac{\Delta (1-a)}{(1-a)}+\frac{\Delta (1+a)}{1+a}\)
⇒ \(\frac{\Delta r}{r}=\frac{\Delta a}{1-a}+\frac{\Delta a}{1+a}=\frac{\Delta a(1+a+1-a)}{(1-a)(1+a)}\)
Question
In an experiment the initial number of radioactive nuclei is 3000. It is found that 1000 ± 40 nuclei decayed in the first 1.0 s. For \(\left | x \right |\ll 1\), In (1 +x)=x up to first power in x. The
error \(\Delta \lambda \), in the determination of the decay constant λ, in s-1, is
(a) 0.04 (b) 0.03 (c) 0.02 (d) 0.01
10 Subjective Problems
Answer/Explanation
Ans.
(c)
(c) Using, \(N={N_{0^{e}}}^{-\lambda t}\Rightarrow 1n N=1nN_{0}-\lambda t\)
Differentiation with respect to λ
⇒ \(\frac{1}{N}\frac{dN}{d\lambda }= 0-t\)
Question
If nth division of main scale coincides with (n+l )th divisions of vernier scale. Given one main scale division is equal to ‘a’ units. Find the least count ofthe vernier.
Answer/Explanation
Ans.
\(\left ( \frac{a}{n+1} \right )\)
(n + 1) V.S.D = n M.S.D
∴ 1 V.S.D = \(\frac{n}{n+1}M.S.D\)
Least count, (L.C.) = 1 M.S.D- 1 V.S.D
= \(\left ( 1-\frac{n}{n+1} \right )M.S.D\)
