Question
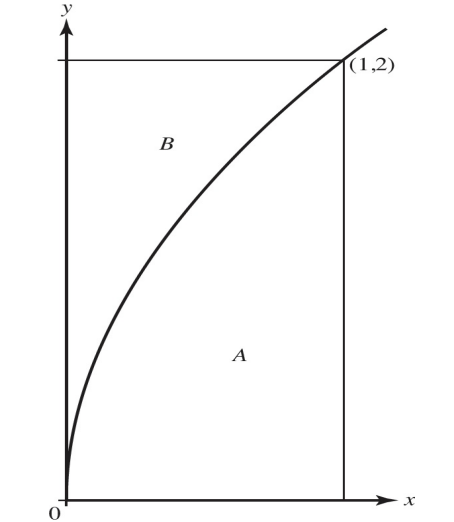
The curve $y=\sqrt{8 \sin \left(\frac{\pi x}{6}\right)}$ divides a first-quadrant rectangle into regions $\boldsymbol{A}$ and $\boldsymbol{B}$, as shown in the figure above.
(a) Region $\boldsymbol{A}$ is the base of a solid. Cross sections of this solid perpendicular to the $x$-axis are rectangles. The height of each rectangle is 5 times the length of its base in region $\boldsymbol{A}$. Find the volume of this solid.
(b) The other region, $\boldsymbol{B}$, is rotated around the $y$-axis to form a different solid. Set up, but do not evaluate, an integral for the volume of this solid.
▶️Answer/Explanation
(a) The rectangular slices have base $y$, height $5 y$, and thickness along the $x$-axis:
$
\Delta V=(y)(5 y) \Delta x=5 y^2 \Delta x=5\left(\sqrt{8 \sin \left(\frac{\pi x}{6}\right)}\right)^2 \Delta x
$
For the $\mathrm{AB}$ exam, this question is calculator active; therefore,
$
V=40 \int_0^1 \sin \left(\frac{\pi x}{6}\right) d x=10.235(\text { or 10.234) }
$
For the BC exam, this question is no calculator; so the integral must be calculated by hand, as follows:
$
\begin{aligned}
V & =40 \int_0^1 \sin \left(\frac{\pi x}{6}\right) d x=40 \frac{6}{\pi} \int_0^1 \sin \left(\frac{\pi x}{6}\right)\left(\frac{\pi}{6} d x\right) \\
& =-\left.\frac{240}{\pi} \cos \left(\frac{\pi x}{6}\right)\right|_0 ^1=-\frac{240}{\pi}\left(\cos \left(\frac{\pi}{6}\right)-\cos (0)\right) \\
& =\frac{240}{\pi}\left(1-\frac{\sqrt{3}}{2}\right)
\end{aligned}
$
(b) The disks have radius $x$ and thickness along the $y$-axis:
$
\Delta V=\pi x^2 \Delta y, \text { so } V=\pi \int_0^2 x^2 d y
$
Now we solve for $x$ in terms of $y$ :
$
y=\sqrt{8 \sin \left(\frac{\pi x}{6}\right)}, \text { so } y^2=8 \sin \left(\frac{\pi x}{6}\right) \text { and } \frac{y^2}{8}=\sin \left(\frac{\pi x}{6}\right)
$
Then $\arcsin \frac{y^2}{8}=\left(\frac{\pi x}{6}\right)$, which gives us $x=\frac{6}{\pi} \arcsin \frac{y^2}{8}$.
Therefore $V=\pi \int_0^2\left(\frac{6}{\pi} \arcsin \frac{y^2}{8}\right)^2 d y$.
(NOTE: Although the shells method is not a required AP topic, another correct integral for this volume is
$
\left.V=2 \pi \int_0^1 x\left(2-\sqrt{8 \sin \frac{\pi x}{6}}\right) d x .\right)
$
