Question
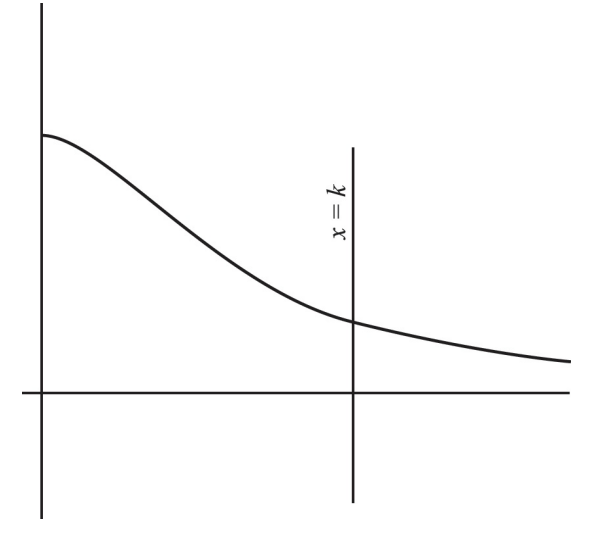
Consider the first-quadrant region bounded by the curve $y=\frac{18}{9+x^2}$, the coordinate axes, and the line $x=k$, as shown in the figure above.
(a) For what value of $k$ will the area of this region equal $\Pi$ ?
(b) What is the average value of the function on the interval $0 \leq x \leq k$ ?
(c) What happens to the area of the region as the value of $k$ increases?
▶️Answer/Explanation
(a) $\begin{aligned} \int_0^k \frac{18}{9+x^2} d x & =\pi \\ 3 \cdot \frac{18}{9} \int_0^k \frac{\frac{1}{3} d x}{1+\left(\frac{x}{3}\right)^2} & =\pi \\ \left.6 \arctan \frac{x}{3}\right|_0 ^k & =\pi \\ 6 \arctan \frac{k}{3}-6 \arctan \frac{0}{3} & =\pi \\ \frac{k}{3} & =\tan \frac{\pi}{6} \\ k & =\sqrt{3}\end{aligned}$
(b) The average value of a function on an interval is the area under the graph of the function divided by the interval width, here $\frac{\pi}{\sqrt{3}}$
(c) From part (a) you know that the area of the region is given by $\int_0^k \frac{18}{9+x^2} d x=6 \arctan \frac{k}{3}$.
Since $\lim _{k \rightarrow \infty} 6 \arctan \frac{k}{3}=6\left(\frac{\pi}{2}\right)=3 \pi$, as $k$ increases the area of the region approaches 3п.
