Question
$\lim _{x \rightarrow \infty} \frac{20 x^2-13 x+5}{5-4 x^3}$ is
(A) $-5$
(B) 0
(C) 1
(D) $\infty$
▶️Answer/Explanation
Ans:B
Use the Rational Function Theorem
A rational function is of the form
$
f(x)=\frac{P(x)}{Q(x)}
$
where $P(x)$ and $Q(x)$ are polynomials. The domain of $f$ is the set of all reals for which $Q(x) \neq 0$.
Question
$\lim _{h \rightarrow 0} \frac{\ln (2+h)-\ln 2}{h}$ is
(A) $\ln 2$
(B) $\frac{1}{2}$
(C) $\frac{1}{\ln 2}$
(D) $\infty$
▶️Answer/Explanation
Ans:B
Note that $\lim _{h \rightarrow 0} \frac{\ln (2+h)-\ln 2}{h}=f^{\prime}(2)$, where $f(x)=\ln x$.
Question
If $y=e^{-x^2}$, then $y^{\prime \prime}(0)$ equals
(A) 2
(B) 1
(C) 0
(D) $-2$
▶️Answer/Explanation
Ans:D
Since $y^{\prime}=-2 x e^{-x^2}$, therefore $y^{\prime \prime}=-2\left(x \cdot e^{-x^2} \cdot(-2 x)+e^{-x^2}\right)$. Replace $x$ by 0 .
Question
Use the following table, which shows the values of the differentiable functions $f$ and $g$.
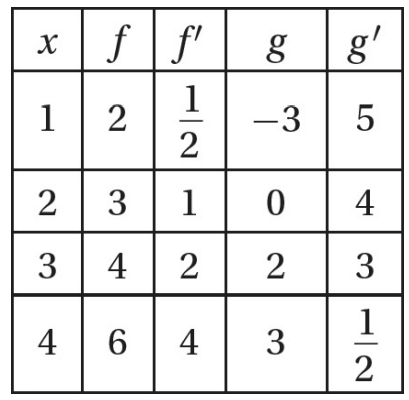
The average rate of change of function $f$ on $[1,4]$ is
(A) $7 / 6$
(B) $4 / 3$
(C) $15 / 8$
(D) $15 / 4$
▶️Answer/Explanation
Ans:B
$\frac{f(4)-f(1)}{4-1}=\frac{6-2}{4-1}=\frac{4}{3}$
Question
Use the following table, which shows the values of the differentiable functions $f$ and $g$.

If $h(x)=g(f(x))$ then $h^{\prime}(3)=$
(A) $1 / 2$
(B) 1
(C) 4
(D) 6
▶️Answer/Explanation
Ans:B
$h^{\prime}(3)=g^{\prime}(f(3)) \cdot f^{\prime}(3)=g^{\prime}(4) \cdot f^{\prime}(3)=\frac{1}{2} \cdot 2$
