Question
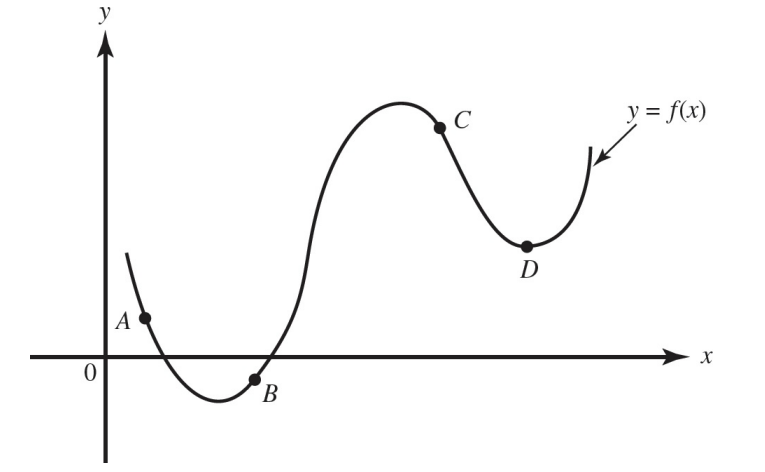
At which point on the graph of $y=f(x)$ shown above is $f(x)<0$ and $f^{\prime}(x)>0$ ?
(A) $A$
(B) $B$
(C) $C$
(D) $D$
▶️Answer/Explanation
Ans:A
The curve falls when $f^{\prime}(x)<0$ and is concave up when $f^{\prime \prime}(x)>0$.
Question
Which best describes the behavior of the function $y=\arctan \left(\frac{1}{\ln x}\right)$ at $x=1$ ?
(A) It has a jump discontinuity.
(B) It has an infinite discontinuity.
(C) It has a removable discontinuity.
(D) It is continuous.
▶️Answer/Explanation
Ans:A
(A) Selecting an answer for this question from your calculator graph is unwise. In some windows the graph may appear continuous; in others there may seem to be cusps, or a vertical asymptote. Put the calculator aside. Find
$
\lim _{x \rightarrow 1^{+}}\left(\arctan \left(\frac{1}{\ln x}\right)\right)=\frac{\pi}{2} \text { and } \lim _{x \rightarrow 1^{-}}\left(\arctan \left(\frac{1}{\ln x}\right)\right)=-\frac{\pi}{2}
$
These limits indicate the presence of a jump discontinuity in the function at $x=1$.
Question
Let $G(x)=[f(x)]^2$. In an interval around $x=a$, the graph of $f$ is increasing and concave downward, while $G$ is decreasing. Which describes the graph of $G$ there?
(A) concave downward
(B) concave upward
(C) point of inflection
(D) quadratic
▶️Answer/Explanation
Ans:B
(B) We are given that (1) $f(a)>0$; (2) $f^{\prime}(a)<0$; and (3) $G^{\prime}(a)<0$. Since $G^{\prime}(x)=2 f(x) \cdot f(x)$, therefore $G^{\prime}(a)=2 f(a)$. $f(a)$. Conditions (1) and (3) imply that $(4) f(a)<0$.
Since $G^{\prime \prime}(x)=2\left[f(x) \cdot f^{\prime \prime}(x)+(f(x))^2\right]$, therefore $G^{\prime \prime}(a)=2\left[f(a) f^{\prime \prime}(a)+(f(a))^2\right]$. Then the sign of $G^{\prime \prime}(a)$ is $2[(-) \cdot(-)+$ $(+)]$ or positive, where the minus signs in the parentheses follow from conditions (4) and (2).
Question
The value of $c$ for which $f(x)=x+\frac{c}{x}$ has a local minimum at $x=3$ is
(A) $-9$
(B) 0
(C) 6
(D) 9
▶️Answer/Explanation
Ans:D
Since $f^{\prime}(x)=1-\frac{c}{x^2}$, it equals 0 for $x=\pm \sqrt{c}$. When $x=3, c=9$; this yields a minimum since $f^{\prime}(3)>0$.
Question
The function $g$ is a differentiable function. It is known that $g^{\prime}(x) \leq 4$ for $3 \leq x \leq 10$ and that $g(7)=8$. Which of the following could be true?
I. $g(5)=0$
II. $g(8)=-4$
III. $g(9)=17$
(A) I only
(B) II only
(C) I and II only
(D) I and III only
▶️Answer/Explanation
Ans:C
We can define function $g$ as $g(x)=g(7)+\int_7^x g^{\prime}(t) d t$. We will use this definition for $g(x)$ and the fact that we can find the maximum value of an integral over an interval by using one rectangle with the height equal to the maximum value of the function over the interval and the width equal to the width of the interval. We were given the maximum value of $g^{\prime}(x)$ on $3 \leq x \leq 10$.
I. $g(5)=g(7)+\int_7^5 g^{\prime}(x) d x \leq 8+(4)(-2)=0$; therefore $g(5)=0$ is possible.
II. $g(8)=g(7)+\int_7^8 g^{\prime}(x) d x \leq 8+(4)(1)=12$; therefore $g(8)=-4$ is possible.
III. $g(9)=g(7)+\int_7^9 g^{\prime}(x) d x \leq 8+(4)(2)=16$; therefore $g(9)=17$ is not possible.
