Question
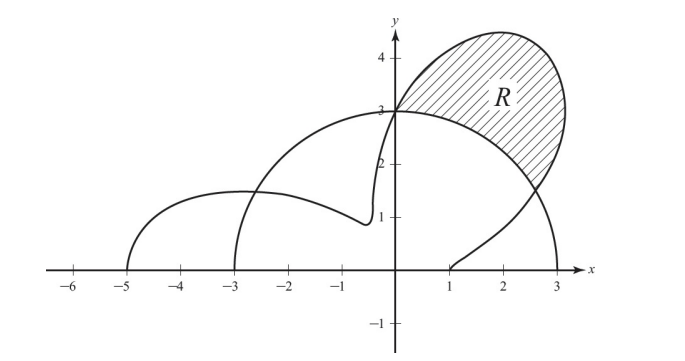
Shown above are the graphs of the polar curves $r=3$ and for $r=3-2 \cos (3 \theta)$ for $0 \leq \theta \leq \pi$. Region $R$ is the shaded region inside the graph of $r=3-2 \cos (3 \theta)$ and outside the graph of $r=3$. The two curves intersect at $\theta=\frac{\pi}{6}, \theta=\frac{\pi}{2}$, and $\theta=\frac{5 \pi}{6}$
(a) Write, but do not evaluate, an integral expression for the area of region $R$.
(b) For the graph of $r=3-2 \cos (3 \theta)$, write expressions for $\frac{d x}{d \theta}$ and $\frac{d y}{d \theta}$ and in terms of $\theta$.
(c) Write an equation, in terms of $x$ and $y$, for the tangent line to the curve $r=3-2 \cos (3 \theta)$ when $\theta=\frac{\pi}{2}$. Show the computations that lead to your answer.
▶️Answer/Explanation
(a) $\frac{1}{2} \int_{\pi / 6}^{\pi / 2}\left((3-2 \cos (3 \theta))^2-3^2\right) d \theta$ $\frac{d r}{d \theta}=6 \sin (3 \theta), x=r \cos \theta$, and $y=r \sin \theta$
(b) $\frac{d x}{d \theta}=\frac{d r}{d \theta} \cos \theta-r \sin \theta \Rightarrow \frac{d x}{d \theta}=6 \sin (3 \theta) \cos \theta-(3-2 \cos (3 \theta)) \sin \theta$
$
\frac{d y}{d \theta}=\frac{d r}{d \theta} \sin \theta+r \cos \theta \Rightarrow \frac{d y}{d \theta}=6 \sin (3 \theta) \sin \theta+(3-2 \cos (3 \theta)) \cos \theta
$
(c) The slope of the tangent line is $\frac{d y}{d x}=\frac{d y / d \theta}{d x / d \theta}$. When $\theta=\frac{\pi}{2}$, then $r\left(\frac{\pi}{2}\right)=3-2 \cos \left(\frac{3 \pi}{2}\right)=3 \Rightarrow x=3 \cos \left(\frac{\pi}{2}\right)=0 \Rightarrow y=3 \sin \left(\frac{\pi}{2}\right)=3$.
$
\left.\frac{d y}{d x}\right|_{\theta=\pi / 2}=\left.\frac{d y / d \theta}{d x / d \theta}\right|_{\theta=\pi / 2}=\frac{6 \sin \left(\frac{3 \pi}{2}\right) \sin \left(\frac{\pi}{2}\right)+\left(3-2 \cos \left(\frac{3 \pi}{2}\right)\right) \cos \left(\frac{\pi}{2}\right)}{6 \sin \left(\frac{3 \pi}{2}\right) \cos \left(\frac{\pi}{2}\right)-\left(3-2 \cos \left(\frac{3 \pi}{2}\right)\right) \sin \left(\frac{\pi}{2}\right)}=\frac{-6}{-3}=2
$
The tangent line is $y=3+2(x-0)=3+2 x$.
