Question
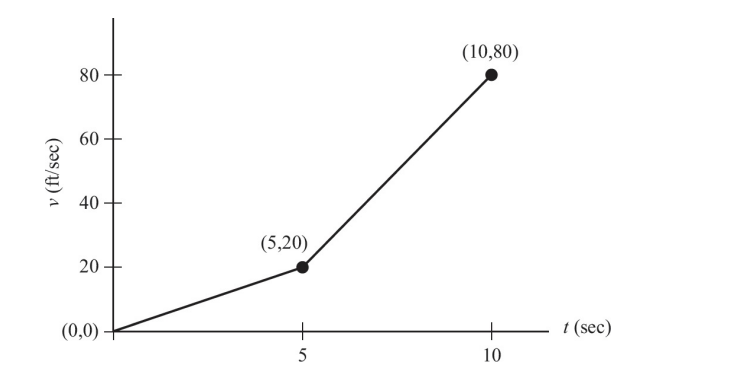
Two autos, $P$ and $Q$, start from the same point and race along a straight road for 10 seconds. The velocity of $P$ is given by $v_p(t)=6(\sqrt{1+8 t}-1)$ feet per second. The velocity of $Q$ is shown in the graph.
(a) At what time is $P^{\prime}$ s actual acceleration (in $\mathrm{ft} / \mathrm{sec}^2$ ) equal to its average acceleration for the entire race?
(b) What is $Q^{\prime}$ s acceleration (in $\mathrm{ft} / \mathrm{sec}^2$ ) then?
(c) At the end of the race, which auto was ahead? Explain.
▶️Answer/Explanation
(a) $v_p(t)=6(\sqrt{1+8 t}-1)$, so $v(0)=0$ and $v(10)=48$.
The average acceleration is $\frac{\Delta v}{\Delta t}=\frac{48-0}{10-0}=\frac{24}{5} \mathrm{ft} / \mathrm{sec}^2$.
Acceleration $a(t)=v^{\prime}(t)=6 \cdot \frac{1}{2}(1+8 t)^{-\frac{1}{2}}(8) \mathrm{ft} / \mathrm{sec}^2$
$\frac{24}{\sqrt{1+8 t}}=\frac{24}{5}$ when $t=3$ seconds
(b) Since $Q$ ‘s acceleration, for all $t$ in $0 \leq t \leq 5$, is the slope of its velocity graph,
$
a=\frac{20-0}{5-0}=4 \mathrm{ft} / \mathrm{sec}^2 .
$
(c) Find the distance each auto has traveled. For $P$, the distance is
$
\begin{aligned}
\int_0^{10} 6(\sqrt{1+8 t}-1) & = \\
6\left[\frac{1}{8} \int_0^{10} \sqrt{1+8 t} \cdot 8 d t-\int_0^{10} d t\right] & = \\
\left.6\left(\frac{1}{8} \cdot \frac{2}{3}(1+8 t)^{\frac{3}{2}}-t\right)\right|_0 ^{10} & = \\
6\left(\frac{1}{12}\left(81 \frac{3}{2}-1 \frac{3}{2}\right)-10\right) & =304 \text { feet }
\end{aligned}
$
