Question
$\int_1^2(3 x-2)^3 d x$ is equal to
(A) $\frac{64}{3}$
(B) $\frac{63}{4}$
(C) $\frac{85}{4}$
(D) $\frac{255}{4}$
▶️Answer/Explanation
Ans:C
$\frac{1}{3} \int_1^2(3 x-2)^3(3 d x)=\left.\frac{1}{12}(3 x-2)^4\right|_1 ^2$
Question
Given the parametric equations $x(t)=2 t^2-1$ and $y(t)=3+2 t^{3 / 2}$, which expression gives the length of the curve from $t=1$ to $t=3$ ?
(A) $\int_1^3 \sqrt{1+9 t} d t$
(B) $\int_1^3 \sqrt{1+\frac{9}{16 t}} d t$
(C) $\int_1^3 \sqrt{16 t^2+9 t} d t$
(D) $\int_1^3 \sqrt{\left(2 t^2-1\right)^2+\left(3+2 t^{3 / 2}\right)^2} d t$
▶️Answer/Explanation
Ans:C
The length of the curve is $\int_a^b \sqrt{\left(x^{\prime}(t)\right)^2+\left(y^{\prime}(t)\right)^2} d t$. Since $x^{\prime}(t)=4 t$ and $y^{\prime}(t)=3 \sqrt{t}$, the length is
$
\int_1^3 \sqrt{(4 t)^2+(3 \sqrt{t})^2} d t=\int_1^3 \sqrt{16 t^2+9 t} d t
$
Question
What is the radius of convergence for the series $\sum_{n=0}^{\infty} \frac{(x-7)^n}{3^n(n+2)^4}$ ?
(A) $\frac{1}{3}$
(B) 1
(C) 3
(D) 7
▶️Answer/Explanation
Ans:C
Use the Ratio Test to find the radius of convergence.
The ratio is $\left|\frac{(x-7)^{n+1}}{3^{n+1}(n+3)^4} \cdot \frac{3^n(n+2)^4}{(x-7)^n}\right|=\left|\left(\frac{n+2}{n+3}\right)^4 \cdot \frac{x-7}{3}\right|$. Find the limit: $\lim _{x \rightarrow \infty}\left|\left(\frac{n+2}{n+3}\right)^4 \cdot \frac{x-7}{3}\right|=\left|\frac{x-7}{3}\right|$. So for convergence, $\left|\frac{x-7}{3}\right|<1 \Rightarrow|x-7|<3$. Therefore, the radius of convergence is 3 .
Question
Which equation has the slope field shown below?
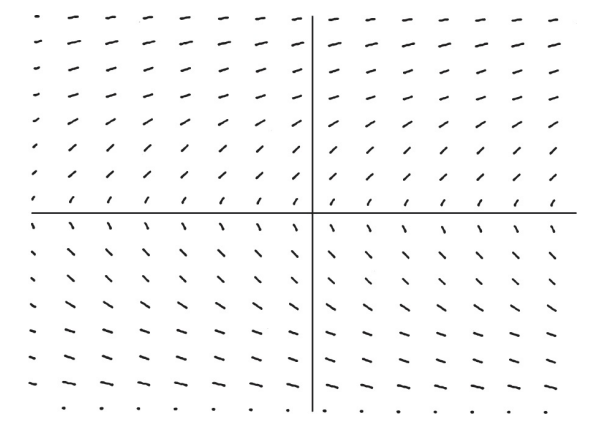
(A) $\frac{d y}{d x}=\frac{5}{y}$
(B) $\frac{d y}{d x}=\frac{5}{x}$
(C) $\frac{d y}{d x}=\frac{x}{y}$
(D) $\frac{d y}{d x}=5 y$
▶️Answer/Explanation
Ans:A
Question
Consider the function $h$ that is continuous on the closed interval $[2,6]$ such that $h(4)=5$ and $h(6)=13$. Which of the following statements must be true?
(A) $h$ is increasing on the interval $[4,6]$.
(B) $h^{\prime}(x)=4$ has at least one solution in the interval $(4,6)$.
(C) $5 \leq h(5) \leq 13$.
(D) $h(x)=12$ has at least one solution in the interval $[4,6]$.
▶️Answer/Explanation
Ans:D
Since the function $h$ is continuous on the interval $[4,6], h(4)=5$, and $h(6)=13$, the Intermediate Value Theorem tells us that all function values between 5 and 13 must exist on that interval. Therefore, there must be an $x$-value on that interval where $h(x)=12$. NOTE: Choice (A) doesn’t have to be true-the function could be both increasing and decreasing on some subintervals of $[4,6]$. Choice (B) may not be true if $h$ is not differentiate on $(4,6)$. Choice (C) may not be true-the function may dip below 5 and then rise back up to 13 on the interval $[4,6]$.
