Question
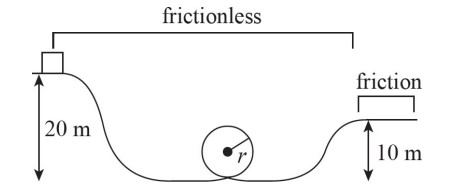
A roller coaster cart rides along the track shown above. The initial drop, the loop, and the ascending ramp are all frictionless. The flat portion of the track after the ascending ramp is not frictionless.
(a) How fast would the cart be moving just before it enters the loop?
(b) Would the normal force on the cart be greater just after entering the loop or at the peak of the loop? Explain why using relevant equations.
(c) What is the greatest possible radius for the loop that would allow the cart to still make it through?
(d) If the coefficient of static friction for the final segment of the track is 0.2, how long does the segment need to be to allow the cart to come to a complete stop due to friction alone?
▶️Answer/Explanation
Ans:
(a) Using conservation of energy, we set the potential energy at the top of the ramp equal to the kinetic energy at the bottom to get \(mgh=\frac{1}{2}mv^{2}\). Solving for v gives \(v=\sqrt{2gh}=\sqrt{(2)(10)(20)}=\sqrt{400}=20m/s\).
(b) Throughout the entire loop, there are only two forces acting on the cart: \(F_{g}\) and \(F_{N}\). The loop can be considered as a case of uniform circular motion, so the net force will always be directed toward the center and will be equal to \(\frac{mv^{2}}{r}\). At the bottom of the loop, that means \(\frac{mv^{2}}{r}=F_{N}-F_{g}\), so \(F_{N}=\frac{mv^{2}}{r-F_{g}}\). At the top of the loop, \(\frac{mv^{2}}{r}=F_{N}+F_{g}\), so \(F_{N}=\frac{mv^{2}}{r-F_{g}}\). Thus, the normal force must always be greater at the bottom of the loop.
(c) Mechanical energy will be constant throughout since the track is frictionless, so set the energy at the beginning equal to the energy at the top of the loop. This gives \(mgh=mg(2r)+\frac{1}{2}mv^{2}\), where r is the radius of the circle and v is the speed at the top of the loop.
Next, recall that in order for the car to complete the loop, it must be going fast enough to create some normal force at the top. In general, this equation would look like \(\frac{mv^{2}}{r}=F_{N}+F_{g}\). Maximizing the loop means setting \(F_{N}=0\), so \(\frac{mv^{2}}{r}=mg\). Moving the r to the other side gives \(mv^{2}=mgr\). Substituting this value into the first equation gives \(mgh=mg(2r)+\frac{1}{2}(mgr)\). You can cancel out m and g since they appear in every term, so \(h=2r+\frac{1}{2}r=2.5r\). The problem shows h = 20, so solving for r gives r = h/(2.5) = (20)/(2.5) = 8 m.
(d) Conservation of energy can be used to find the speed of the car as it enters the final segment. Set the potential energy of the initial position equal to the potential and kinetic energies as the cart enters the final stretch. This gives \(mgh_{1}=mgh_{2}+\frac{1}{2}mv^{2}\). First, realize m can be dropped since it appears in every term. Solving for v then gives \(v=\sqrt{2g}(h_{1}-h_{2})=\sqrt{(2)(10)(20-10)}=\sqrt{200}=10\sqrt{2}m/s\).
In order for the friction to bring the cart to a stop, it must do work to the cart. We know \(W=\Delta KE\), so \(Fd\cos \theta=\frac{1}{2}mv{_{0}}^{2}\). The first KE term can be dropped since the final speed will be 0. We can substitute \(F_{f}=\mu F_{N}=\mu mg\) for F term since friction is the force doing the work. Additionally, θ = 180° because the frictional force will act in a direction opposite the cart’s motion. All of this gives \((\mu mg)d\cos180^{\circ}=\frac{1}{2}mv{_{0}}^{2}\). Canceling the m on each side and solving for d then gives \(d=-\frac{1}{2}v{_{0}}^{2}/(\mu g\cos180^{\circ})=-\frac{\frac{1}{2}(10\sqrt{2})^{2}}{(0.2)(10)(-1)}=50m\).
Question
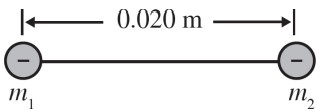
In the above diagram, two small objects, each with a charge of –4.0 nC, are held together by a 0.020 m length of insulating string. The objects are initially at rest on a horizontal, non-conducting, frictionless surface. The effects of gravity on each other can be considered negligible.
(a) Calculate the tension in the string.
(b) Illustrate the electric field by drawing electric field lines for the two objects on the following diagram.
![]()
The masses of the objects are \(m_{1}\) = 0.030 kg and \(m_{2}\) = 0.060 kg. The string is now cut.
(c) Calculate the magnitude of the initial acceleration of each object.
(d) On the axes below, sketch a graph of the acceleration a of the object of mass m2 versus the distance d between the objects after the string has been cut.

(e) In a brief paragraph, describe the speed of the objects as time increases, assuming that the objects remain on the horizontal, non-conducting frictionless surface.
▶️Answer/Explanation
Ans:
(a) Applying Newton’s Second Law to one of the objects
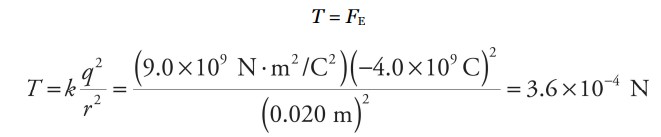
(b) 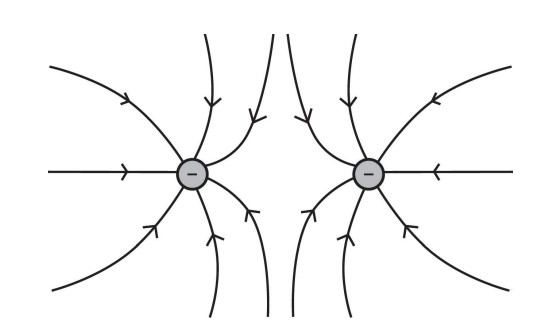
(c) The acceleration is caused by the electrostatic force, and initially that force has the same magnitude as the one calculated in part (A).
\(F_{net}=F_{E}=T\)
\(ma=T\)
Now calculate the acceleration on each object,
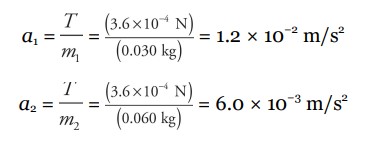
(d) 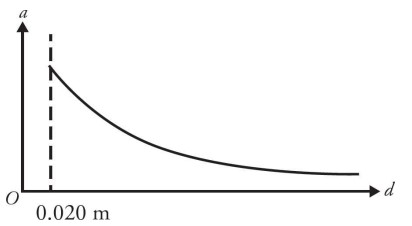
(e) As time increases, the speed of the objects increase. The objects move further apart, but their speeds increase at a slower rate. This is because the electrostatic force decreases as the objects move further apart. Hence, the acceleration also decreases. The speed approaches a constant value as the distance between the objects, d, approaches infinity.
