Question

A car of known mass \(m_{1}\) will collide with a second car of known mass \(m_{2}\). The collision will be head on, and both cars will only move linearly both before and after the collision. In a clear, coherent, paragraph-length response, explain a method for determining whether the collision is perfectly elastic, perfectly inelastic, or neither. If the collision is perfectly inelastic, include at least one possible cause of energy loss.
▶️Answer/Explanation
Ans:
The defining characteristic of a perfectly elastic collision is that no kinetic energy is lost. Therefore, you must record the speeds of each car before and after the collision. Then, the equation \(\frac{1}{2}m_{1}v^{2}_{1,0}+\frac{1}{2}m_{1}v^{2}_{1,f}=\frac{1}{2}m_{2}v^{2}_{2,f}\) can be used to check whether or not it is elastic. The defining feature of a perfectly inelastic collision is that the objects stick together after the collision. This can be simply observed. If the two cars remain intact post-collision, then the collision is perfectly inelastic. If neither of the above is true, then it is neither perfectly elastic nor perfectly inelastic.
Finally, a few possible sources of energy loss would be the heat generated as metal is warped, the sound made by the crash, and even the light of any sparks generated.
Question
Two spheres (one hollow, one solid) are placed side by side on an inclined plane and released at the same time. Both spheres roll down the inclined plane without slipping.
(a) Using a free body diagram, explain what force provides the torque allowing the spheres to roll down the inclined plane.
(b) Which sphere reaches the bottom of the inclined plane first and why?
(c) How do the kinetic energies of the two spheres compare at the bottom of the inclined plane?
▶️Answer/Explanation
Ans:
(a) In order for the objects to roll down the incline, there must be a force providing a torque on the two objects. A free body diagram shows that there are three forces acting on the spheres: the weight of the sphere, the normal force, and the force of friction. Torque is given by the equation τ = rFsin(θ), where F is the magnitude of the force, r is the radius, and θ is the angle between r and F. As both the normal force and the weight of the sphere have a radius of 0, the torque must be provided by the force of friction.
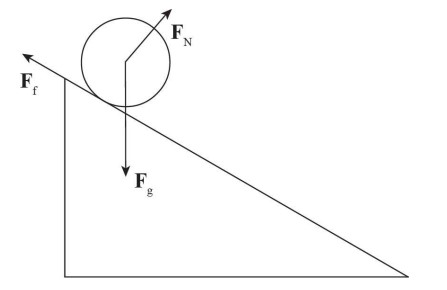
(b) As both objects have the same mass, both objects experience the same normal force and force of friction. This means both objects experience the same torque. Torque in terms of rotational inertia is given by the equation τ = Iα, where I is the rotational inertia and α is the angular acceleration. Because the mass of the hollow sphere is distributed farther from the axis that it rotates around, the hollow sphere has a greater rotational inertia than the solid sphere. With a smaller rotational inertia, the solid sphere experiences a greater angular acceleration and reaches the bottom of the inclined plane first.
(c) As both objects have the same mass and start at the same height (on the top of the inclined plane), they both start with the same amount of potential energy. As both objects also start at rest, they both start with 0 kinetic energy. As the objects reach the bottom of the inclined plane, the potential energy of both objects is converted into kinetic energy. By conservation of energy, both objects have the same kinetic energy at the bottom of the inclined plane
