Question
A 2-kilogram mass is twirled in a vertical circle as shown. It is attached to a 2-meter rope. As the mass just clears the ground (point A ), its velocity is 10 m/s to the right. Neglect any air resistance. When the mass reaches point B , it makes a 30-degree angle to the horizontal as shown.
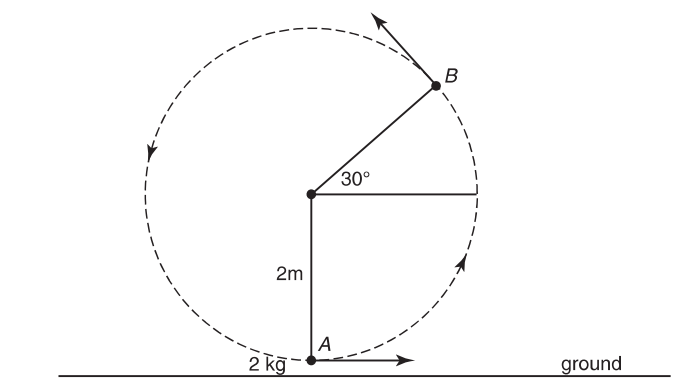
(a) Describe qualitatively, using words and diagrams, the difference in the object’s speed at point B if the twirling is done (i) at constant speed or (ii) at constant
tension. Which would result in the greater speed at point B ? Include an analysis of how the tension must change in part (i).
(b) At point B , the rope is released and the mass becomes a projectile. Assuming the rope has a uniform distribution of mass and remains attached to the flying object. Which of the following options best describe the projectile’s range as compared with a launch without the rope?
_____ addition of rope makes no difference to the range
_____ addition of rope increases the range
_____ addition of rope decreases the range
Explain your reasoning.
(c) When twirling the object at constant speed, explain in terms of work and energy, how the constant speed is maintained. Is the path truly circular when the object’s speed is maintained? In your explanation, be explicit about which forces are doing positive work and which are doing negative work.
▶️Answer/Explanation
Ans:
(a) (i) To maintain constant speed, the tension must be constantly adjusted as the object undergoes its centripetal motion. The tension will be lower at point B than it is at the bottom as there is a component of gravity “helping” the tension in the centripetal direction (as opposed to gravity acting centrifugally at point A):
$\begin{aligned} F_{c A} & =F_{c B}=m v^2 / R \\ T_A-m g & =T_B+m g \sin 30^{\circ}=m v^2 / R \\ T_B & =T_A-m g\left(1+\sin 30^{\circ}\right)\end{aligned}$
(ii) Constant tension will result in a much higher speed at point B as the tension will be locked in at TA above. Since the tension at point B will be higher than in
case (i), mv2/R must be greater as well. Constants m and R mean the speed must be increased.
(b) __X__ addition of rope decreases the range
Although we are ignoring air friction in this problem, we must consider the effect of the additional mass. Although free-fall problems generally ignore mass, the rope will have an effect on the effective launch velocity. The end of the rope directly attached to the twirling mass has the same velocity as the object. However, the rest of the distributed mass is moving at a lower velocity (down to zero at the center of the circle). Therefore, the net effect of the added mass will be to decrease the launch velocity. In addition, recall that the equations of motion actually track the center of mass of an object. Since the center of mass for the combined rope-plus-object system is lower (the mass of the rope extends below the 2 kg mass), the combined rope-plus object system is effectively being launched from a lower height. A lower launch velocity from a lower height will result in a shorter range for the projectile.
(c) While on the way up during the circular motion, the force due to gravity is doing negative work. The component of weight that is tangent does this negative work. Therefore to maintain the same kinetic energy, the tension must do some positive work. In order to accomplish this, the tension must supply an upward tangent component as well, i.e., the circle cannot be perfect. On the downward half of the circular motion, the positive and negative work roles of the tangent components of gravity and tension must reverse.
Question
A small box of mass m is placed on an inclined plane with an angle of incline of θ. There is a coefficient of kinetic friction \(\mu _{k}\) between the inclined plane and the small box. The small box is attached to a much heavier box of mass 3m by a pulley system shown below.
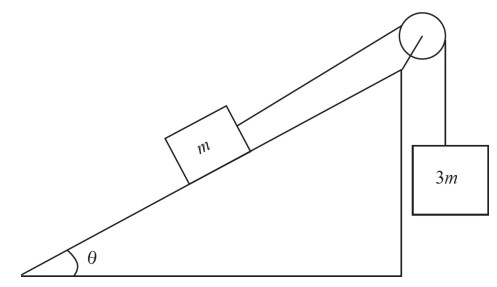
(a) Draw free body diagrams of both masses, including all of the forces acting on each.
(b) Assuming a frictionless, massless pulley, determine the acceleration of the blocks once they are released from rest in terms of \(\mu _{k}\), g, and θ.
(c) If \(\mu _{k}\) = 0.3 and θ = 45°, what distance is traveled by the blocks 3 s after being released from rest?
▶️Answer/Explanation
Ans:
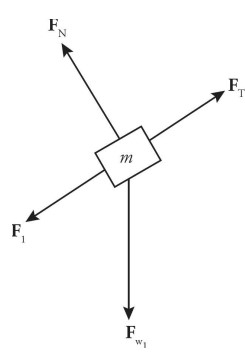
(a) The forces acting on the small m mass are \(F _{T}\) (the tension in the string connecting it to the 3m block), \(F _{w}\) (the weight of the block), \(F _{N}\) (the normal force exerted by the inclined plane), and \(F _{f}\) (the force of kinetic friction).
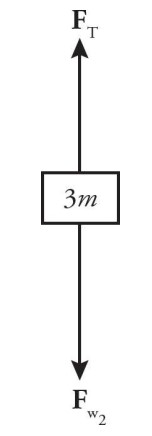
The forces acting on the larger 3m mass are \(F _{T}\) (the tension in the string connecting it to the m block) and \(F _{w}\) (the weight of the block).
(b) Newton’s Second Law applied to the 3m mass yields
\(F_{w2}-F_{T}=3ma\Rightarrow 3mg-F_{T}=3ma\)
Newton’s Second Law applied to the m yields
\(F_{T}-F_{f}-F_{N}=ma\Rightarrow F_{T}-\mu _{k}mg\sin \theta -mg\cos \theta\)
Adding these two equations together, you find that
\(3mg-\mu _{k} mg\sin \theta -mg\cos \theta =ma+3ma\)
\(3mg-\mu _{k} mg\sin \theta -mg\cos \theta =4ma\)
\(a=\frac{3g-\mu _{k}g\sin \theta -\cos \theta }{4}\)
(c) Plugging in g = 10 m/\(s^{2}\), θ = 45°, and \(\mu _{k}\) = 1.0, the acceleration can be calculated as follows:
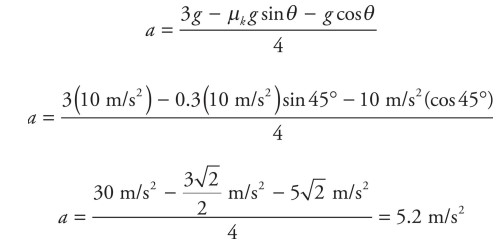
Apply Big Five #3:
\( d=v_{0}t+\frac{1}{2}at^{2}\Rightarrow d=0+\frac{1}{2}(5.2m/s)^{2}=23.4m\)
