Question
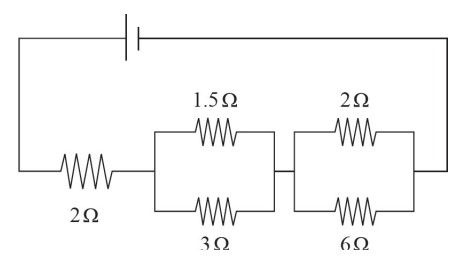
Which of the following circuits would have an equivalent resistance equal to that of the circuit depicted above?
(A) 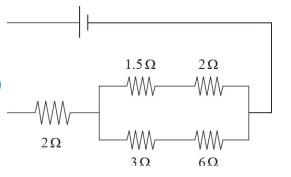
(B) 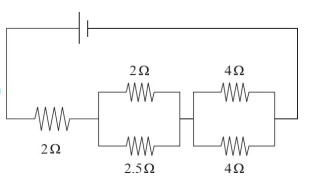
(C) 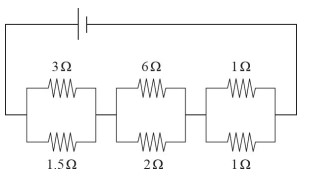
(D) 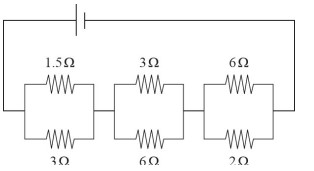
Answer/Explanation
Ans:D
First, find the total resistance of the original circuit. Remember that parallel resistors require you to use the reciprocal sum, while series resistors simply add. For example, the first set of parallel resistors would be combined by doing \(\frac{1}{R}=\frac{1}{1.5}+\frac{1}{3}=1\), which means R = 1 Ω. For the second set of parallel resistors, you would get \(\frac{1}{R}=\frac{1}{2}+\frac{1}{6}=\frac{4}{6}\) , which means R = 1.5 Ω. Adding those two values to the lone series resistor gives \(R_{Total}=\) 2 + 1 + 1.5 = 4.5 Ω. The only answer that matches this value is (D). The first and last set of parallel resistors match the two sets in the original, which means the last parallel set must match the 2 Ω resistor in the original. Solving for that middle parallel set’s combined resistance gives \(\frac{1}{R}=\frac{1}{3}+\frac{1}{6}=\frac{1}{2}\) , which means R = 2 Ω.
Question
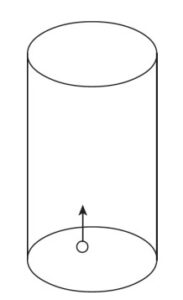
A bubble in a glass of water releases from rest at the bottom of the glass and rises at acceleration a to the surface in t seconds. How much farther does the bubble travel in its last second than in its first second?
(A) at
(B) (t – 1)a
(C) (t + 1)a
(D) \(\frac{1}{2}at\)
Answer/Explanation
Ans:B
The distance travelled in the first second can be found using the Big Five, \(d_{first}=v_{0}t_{first}+\frac{1}{2}at^{2}_{first}\)
Using \(t_{first}\) = 1 s and \(v_{0}\) = 0 m/s since the bubble starts at rest, the equation becomes \( d_{first}=(\frac{1}{2})a\)
The distance traveled in the last second can be found using another Big Five equation. \(d_{last}=v_{final}t_{last}-\frac{1}{2}at^{2}_{last}\)
Using \(t_{last}\) = 1 s and \(v_{final}=v_{0}+at_{total}=at_{total}\), the equation becomes \( d_{last}=at_{total}-(\frac{1}{2})a\)
The question is asking for the difference in the distance, so \(d_{last}-d_{first}=at_{total}-(\frac{1}{2})a-(\frac{1}{2})a=at_{total}-a=(t-1)a\)
Question
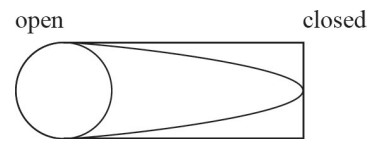
A standing wave is formed in a tube, as shown above. If this wave has a frequency of f, what would be the frequency of the next harmonic that can be formed in this tube?
(A) \(\frac{1}{2}f\)
(B) 2f
(C) 3f
(D) The above wave shows the highest possible harmonic frequency for this system.
Answer/Explanation
Ans:C
Remember that in a system with one closed end and one open end there will be a node at one end and an antinode at the other. From the drawing, you can see that the diagram shows a wave with the greatest possible wavelength in this system. If that is the greatest possible wavelength, then it has the smallest possible, or fundamental, frequency. This type of system cannot make even harmonics, so the next harmonic would be the third, which will be 3f.
Question
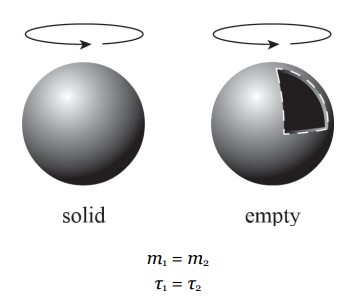
Two spheres of equal size and equal mass are rotated with an equal amount of torque. One of the spheres is solid with its mass evenly distributed throughout its volume, and the other is hollow with all of its mass concentrated at the edges. Which sphere would rotate faster?
(A) Solid sphere
(B) Hollow sphere
(C) They would rotate at equal rates.
(D) Additional information is required to determine the relative rates of rotation.
Answer/Explanation
Ans:A
You know \(T_{Net}=I\alpha\). The torque applied to each is equal, so the sphere with a smaller moment of inertia (I) will rotate more quickly. Moment of inertia is smaller for an object with its mass concentrated closer to the center, so the solid sphere will have a smaller moment of inertia and thus rotate faster.
