Question
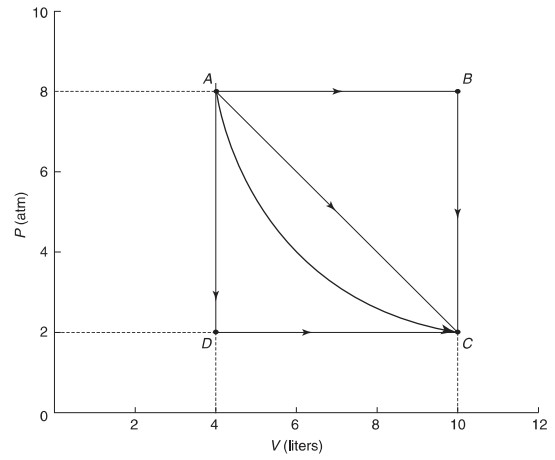
An ideal gas expands from points A to C along three possible paths.
(a) Is it expected that final temperature at point C be path dependent? Justify your answer qualitatively with no calculations.
(b) Discuss and compare the flow of thermal energy along the three paths ( AC , ABC , ADC ). Indicate the direction of heat for each pathway (into or out of the gas) and the relative amount of thermal energy involved. Justify your answer qualitatively with no calculations.
(c) Calculate the work done along path:
i. ABC
ii. AC
iii. ADC
(d) Is there a way to go from A to C with no thermal energy exchanged with the environment? If so, describe and sketch the path on a P – V diagram.
(e) Is there a way to go from A to C with no temperature change? If so, describe and sketch the path on a P – V diagram.
▶️Answer/Explanation
Ans:
(a) No, the temperature is a state function of pressure and volume. So the temperature at point C is not path dependent.
(b) ΔU = Q + W
For an ideal gas, the change in internal energy ( ΔU) is fixed by the change in the temperature. So the difference in thermal energy exchange ( Q ) will be dictated by the amount of work done on each path (see part (c) for a calculation of work). Without doing a calculation, we can visually tell which path is doing more work by examining the areas under the pathways. The product PV is lower at point C than at point A . Therefore, we can conclude that the temperature is lower at point C (ideal gas law PV = nRT ). Since the temperature is decreasing, ΔU is negative while all the work done by the gas represents a loss of energy as well. The difference between the given pathway and an adiabatic expansion (see answer (d)) represents the amount of thermal energy exchanged with the environment ( Q ).
Path AC represents moderate work done by the gas, requiring some thermal energy to be added to the gas during the process but not as much as path ABC , which represents the most work done by the gas. Since pathway ABC is so far from adiabatic, it will require significant thermal energy to be added to the gas. Finally, path ADC is the least amount of work done and the only pathway to require thermal energy to be given to the environment from the gas.
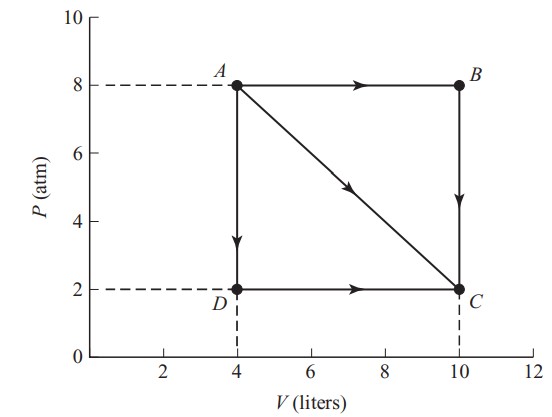
(c) The work done is going to be equal to the area under each segment of the P – V graph. Also recall that 1 atm = 101 kPa = 101,000 N/\(m^{2}\) and 1 L = 0.001 \(m^{3}\):
Pa · \(m^{3}\) = J
i. Along path ABC , no work is done from B → C because there is no change in volume. Thus the area is just the area under AB = (8 atm)(6 L) = 4,848 J.
ii. Along path AC , the total area is equal to:
\(\frac{1}{2}(6atm)(6L)+(2atm)(6L)=3,030J\)
iii. Along path ADC , no work is done from A → D because there is no change in volume. Thus the area is just the area under DC :
(2 atm)(6 L) = 1,212 J
(d) Yes, if the expansion is adiabatic, you can go from A to C with no thermal energy exchanged. This would connect point A and point C with a steep hyperbola. In this case, the work done is solely responsible for the change in internal energy as no heat is involved.
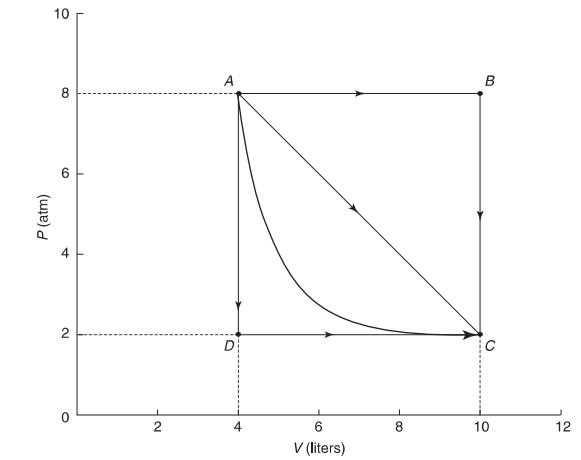
(e) Yes, if the expansion is isothermal, you can go from A to C with no temperature change, In this case, thermal energy will have to be added to the system at the same rate as work is being done by the gas in order to effect no ΔU, This would connect point A and point C with a hyperbola but one less steep than in part (d).