Question
In the laboratory, far from the influence of other magnetic fields, the Earth’s magnetic field has a value of 5.00 × 10−5 T. A compass in this lab reads due north when pointing along the direction of Earth’s magnetic field.
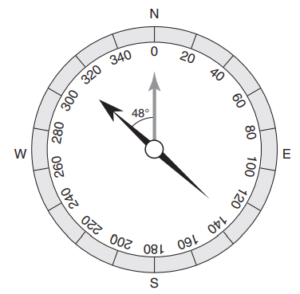
A long, straight current-carrying wire is brought close to the compass, deflecting the compass to the position shown above, 48° west of north.
(a) Describe one possible orientation of the wire and the current it carries that would produce the deflection shown.
(b) Calculate the magnitude Bwire of the magnetic field produced by the wire that would cause the deflection shown.
(c) The distance d from the wire to the compass is varied, while the current in the wire is kept constant; a graph of Bwire vs. d is produced. On the axes below, sketch the shape of this graph.

(d) It is desired to adjust this plot so that the graph becomes a straight line. The vertical axis is to remain Bwire, the magnetic field produced by the wire. How could the quantity graphed on the horizontal axis be adjusted to produce a straight-line graph? Justify your answer.
(e) The current carried by the wire is 500 mA. Determine the slope of the line on the graph suggested in part (d).
▶️Answer/Explanation
Ans(a)
For placing the wire along a north–south line. The wire could be placed above the compass, with the current traveling due north. (The wire also could be placed underneath the compass, with current traveling due south.) (Points can also be earned for an alternative correct solution: for example, the wire could be placed perpendicular to the face of the compass (just south of it), with the current running up.)
(b)
The B field due to Earth plus the B field caused by the wire, when added together as vectors, must give a resultant direction of 48° west of north. Placing these vectors tail-to-tip, as shown below, tan 48° = Bwire/BEarth
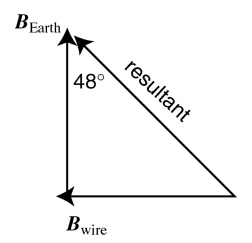
So Bwire = BEarthtan 48° = 5.6 × 10−5 T.
(c)
The magnetic field due to a long, straight, current-carrying wire is given by
\(B=\frac{\mu_{o}I}{2\pi r},\)
where r is the distance from the wire to the field point, represented in this problem by d. So B is proportional to 1/d; this results in a hyperbolic graph. This graph should be asymptotic to both the vertical and horizontal axes.
(d)
Place 1/d on the horizontal axis. The equation for the field due the wire can be written
\(B=\left( \frac{\mu_{o}I}{2\pi r} \right)\left( \frac{1}{d} \right)\)
Everything in the first set of parentheses is constant. So, this equation is of the form y = mx, which is the equation of a line, if 1/d is put on the x-axis of the graph.
(e)
The slope of the graph, from the equation above, is
\(\frac{\mu_{o}I}{2\pi}\)
For plugging in values correctly, including 0.5 A or 500 mA. For units on the slope equivalent to magnetic field times distance (i.e., T·m, T·cm, mT·m, etc.). For a correct answer, complete with correct units: 1.0 × 10−7 Tm, or 1.0 × 10−4mT·m.
