Question
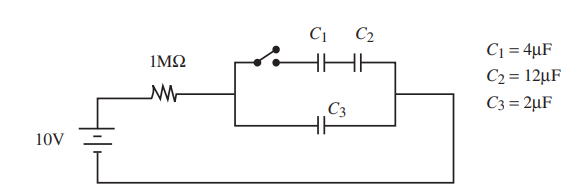
A 1 MΩ resistor is connected to the network of capacitors shown above. The circuit is hooked to a 10-V battery. The capacitors are initially uncharged. The battery is connected, and the switch is closed at time t = 0.
(a) Determine the equivalent capacitance of C1, C2, and C3
(b) Determine the charge on and voltage across each capacitor after a long time has elapsed.
(c) On the axes below, sketch the total charge on C3 as a function of time.
(d) After the capacitors have been fully charged, the switch is opened, disconnecting C1 and C2 from the circuit. What happens to the voltage across and charge on C3? Justify your answer.
▶️Answer/Explanation
(a) The series capacitors add inversely ,
\(\frac{1}{4μF}+\frac{1}{12μF}=\frac{1}{C_{eq}}\)
so \(C_{eq}\) for the series capacitors is 3 μF. The parallel capacitor just adds in algebraically, so the equivalent capacitance for the whole system is 5 μF.
(b)
After a long time, the resistor is irrelevant; no current flows because the fully charged capacitors block direct current. The voltage across \(C_3\) is 10 V (because there’s no voltage drop across the resistor without any current). By Q = CV the charge on \(C_3\) is 20 μC. Treating \(C_1\) and \(C_2\) in series; the equivalent capacitance is 3 μF, the voltage is 10 V
(in parallel with \(C_3\)). The charge on the equivalent capacitance of \(C_1\) and \(C_2\) is 30 μC; thus the charge on \(C_1\) = 30 μC, and the charge on \(C_2\) is also 30 μC (charge on series capacitors is the same).Using Q = CV, the voltage across \(C_1\) is 7.5 V. Using Q = CV, the voltage across C2 is 2.5 V.
(c)
For a graph that starts at Q = 0. For a graph that asymptotically approaches20 μC (or whatever charge was calculated for \(C_3\) in part b). For calculating the time constant of the
circuit, RC = 5 s. For the graph reaching about 63% of its maximum charge after one time constant.
(d)
For recognizing that the voltage does not change. For explaining that if voltage changed, then Kirchoff’s voltage rule would not be valid around a loop including \(C_3\) and the battery (or explaining that voltage is the same across parallel components, so if one is disconnected the other’s voltage is unaffected).
