Question
The diagram below shows two parallel conducting rails connected by a third rail of length L, raised to an angle of 0 with the horizontal (supported by a pair of insulating columns). A metal strip of length L, mass m, and resistance R is free to slide without friction down the rails. The apparatus is immersed in a vertical, uniform magnetic field, B. The resistance of the stationary rails may be neglected.
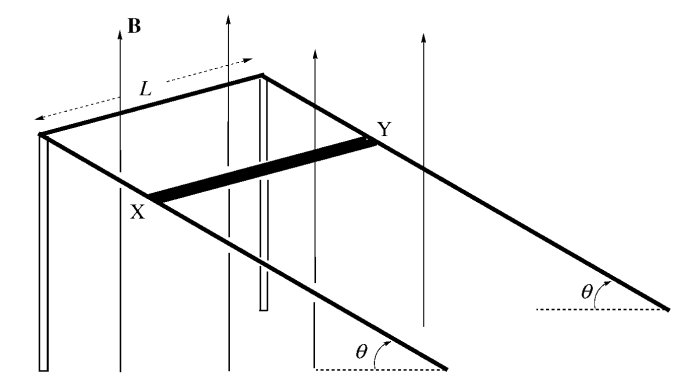
(a) As the strip slides down the rails with instantaneous speed v, determine
(i) the magnitude of the induced emf. (Write your answer in terms of L, B, v, and θ.)
(ii) the direction of the induced current in the strip (X to Y, or Y to X?).
(iii) the magnitude of the induced current. (Write your answer in terms of L, B, R, v, and θ.)
(b) The strip XY will eventually slide down the rails at a constant velocity. Derive an expression for this velocity in terms of L, B, R, m, g, and θ .
(c) When the strip is sliding with the constant velocity determined in part (b), show that the power dissipation in the strip is equal to the rate at which gravity is doing work on the strip.
▶️Answer/Explanation
(a) (i) As the strip XY slides down the rails, the magnetic flux through the rectangular region bounded by the strip increases. This change in magnetic flux induces an emf. If l denotes the distance the strip has slid down the rails, then the magnetic flux through the rectangular region is
\(\Phi _{B}=BA\cos \theta =BLl\cos \theta \)
The rate of change of ΦB is
\(\frac{d\Phi _{B}}{dt}=\frac{d}{dt}(BBl\cos \theta )=BL\cos \theta \frac{dl}{dt}=BL\cos \theta .v\)
where v = df / dt is the speed with which the strip slides. By Faraday’s law, this is the (magnitude of the) induced emf.
(ii)
As the strip slides down, the area increases, so the magnetic flux upward increases. To oppose this change (in accordance with Lenz’s law), the induced current must flow in such a way as to create some magnetic flux downward. By the right-hand rule, then, current must flow from Y to X.
(iii)
The induced current depends on the speed of the sliding strip and is equal to
\(I=\frac{\varepsilon }{R}=\frac{BL\cos \theta .v}{R}\)
(b) In order for the strip to slide with constant velocity, the net force on it must be zero. The force it feels parallel to the rails and downward is Fw sin θ = mg sin θ. The following diagram
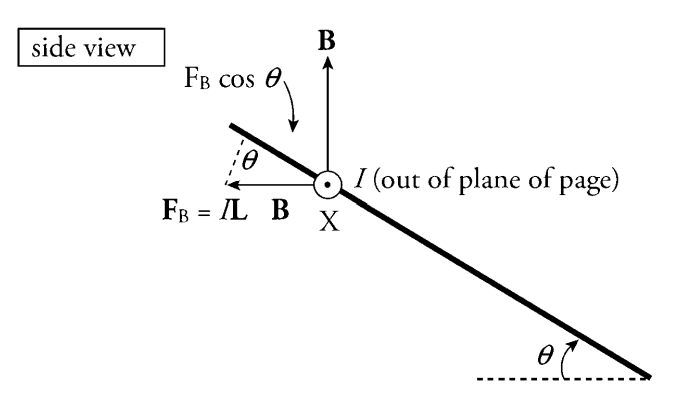
which is a side view of the apparatus looking at the X end of the strip, shows that the force the strip feels parallel to the rails and upward is
\(F_{B}\cos \theta =ILB\cos \theta =\frac{BL\cos \theta .v}{R}LB\cos \theta =\frac{B^{2}L^{2}v \cos ^{2}\theta}{R} \)
The net force on the strip is zero when these two opposing forces balance; the speed at which this occurs will be denoted
\(\upsilon_{f}\)
\(\frac{B^{2}L^{2}\upsilon _{f}\cos ^{2}\theta }{R}=mg \sin \theta \)
\(\upsilon _{f}=\frac{mgR\sin \theta }{B^{2}L^{2}\cos ^{2}\theta }\)
(c) The rate at which thermal energy is produced in the strip is I2 R. When v = Vf, this is equal to
\(P_{dissipated \ by \ strip}=I^{2}R\)
\(=\left ( \frac{BL\cos \theta }{R}.\nu _{f} \right )^{2}R\)
\(=\left ( \frac{BL\cos \theta }{R}.\frac{mgR\sin \theta }{B^{2}L^{2}\cos ^{2}\theta } \right )^{2}R\)
\(=\frac{m^{2}g^{2}R\sin ^{2}\theta }{B^{2}L^{2}\cos ^{2}\theta }\)
\(=\frac{mgR\sin \theta }{B^{2}L^{2}\cos ^{2}\theta }.mg\sin \theta \)
\(\nu _{f}.mg\sin \theta \)
\(\nu _{f}.(F_{w}\sin \theta )\)
= rate at which gravity does work on strip
where the last equality follows from the formula P = Fv for the power produced by a constant force F acting on an object whose velocity, v, is parallel to F.
