Question
A 30 µF capacitor has 6 millicoulombs of charge on each plate. The energy stored in the capacitor is most nearly
(A) 5.4 $\times $ 10-10 J
(B) 9.0 $\times $10-8 J
(C) o.6 J
(D) 12.5 J
(E) 100 J
▶️Answer/Explanation
Ans: C
The energy stored in a capacitor is given by the equations
\(U_{c}=\frac{1}{2}QV=\frac{1}{2}CV^{2}=\frac{Q^{2}}{2C}\)
Select the last part of the equation because the charge, in millicoulombs, and the capacitance, in microfarads, are given. The solution is shown below
\(U_{c}=\frac{(6\times 10^{-3})^{2}}{2(30\times 10^{-6})}=0.6J\)
Question
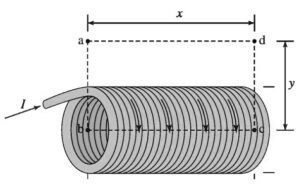
An ideal solenoid with N total turns has a current J passing through the helical wires that make up the solenoid. Ampere’s law is used with a rectangular path abed as shown above, to calculate the magnitude of the magnetic field B within the solenoid. The horizontal distances of the path are length x and the vertical distances of the path are length y. Which of the following equations results from the correct application of Ampere’s law in this situation?
(A) B(2x + 2y) = \(\mu _{o}NI\)
(B) B(2x) = \(\mu _{o}NI\)
(C) B(x + 2y) = \(\mu _{o}NI\)
(D) B(2y) = \(\mu _{o}NI\)
(E) B(x) = \(\mu _{o}NI\)
▶️Answer/Explanation
Ans: E
Ampere’s law is \(\oint B.d\ s=\mu _{o}I\). For an ideal solenoid the magnetic field is uniform and directed along the central axis within the solenoid and zero outside. In this case, only segment be contributes to the integral because ad is outside the solenoid where the field is zero and ab and cd are perpendicular to the field, so the dot product of those segments with B is zero. The number of times the current will pass through our path is equal to the number of coils in the solenoid. This gives us the equation \(B(x)=\mu _{o}NI\)
Question
Two large, parallel conducting plates have a potential difference of V maintained across them. A proton starts at rest on the surface of one plate and accelerates toward the other plate. Its acceleration in the region between the plates is proportional to
(A) \(\frac{1}{V}\)
(B) \(\frac{1}{\sqrt{V}}\)
(C) \(\sqrt{V}\)
(D) V
(E) V2
▶️Answer/Explanation
Ans: D
The electric field is uniform in between the plates, so the force and the acceleration are constant. Relating the potential difference to the electric field gives us \(\Delta V=-Ex\), where x is the separation of the plates. The definition of the electric field is the force divided by the charge. Use these two pieces of information and Newton’s Second Law to solve for the acceleration in terms of V.
\(E=\frac{F}{q}\)
\(\frac{V}{x}=\frac{F}{q}\)
\(\frac{Vq}{x}=ma\)
\(\frac{Vq}{mx}=a\)
This shows the acceleration is directly proportional to the potential difference V.
Questions (a)-(b)
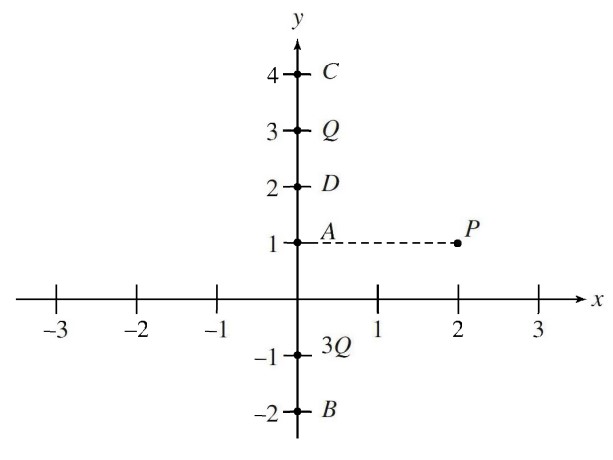
Particles of charge +3Q and +Q are located on the y-axis as shown above. Assume the particles are isolated from other particles and are stationary. A, B, C, D, and P are points in the plane as indicated in the diagram.
Question(a)
Which of the following describes the direction of the electric field at point P?
(A) +x direction
(B) -y direction
(C) components in both the +x and-y direction
(D) components in both-x and +y direction
(E) components in both +x and +y direction
▶️Answer/Explanation
Ans: E
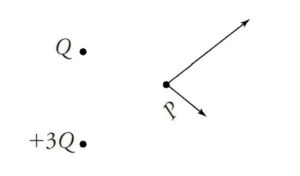
The electric field will radiate outward from both +3Q and +Q, and the field due to the +3Q charge will be greater because point P is the same distance for both charges. This vector diagram is shown below. The resultant will be in the+x and +y directions.
Question(b)
At which of the labeled points is the electric potential zero?
(A)A
(B)B
(C) C
(D)D
(E) None of the points
▶️Answer/Explanation
Ans:E
The electric potential can be calculated using the equation\(V=\sum \frac{kQ}{r}\). Because there are only positive charges, the
electric potential due to each charge will be positive, so the sum cannot be zero.
