Question
For a particular nonlinear spring, the relationship between the magnitude of the applied force, F, and the stretch of the spring, x, is given by the equation \(F = kx^{1.5}\). How much energy is stored in the spring when is it stretched a distance \(x_1\)
(A) \(\frac{2k_1^{2.5}}{5}\)
(B) \(\frac{kx_1^{1.5}}{5}\)
(C) \(kx_1^{2.5}\)
(D) \(\frac{1}{2}kx_1^2\)
(E) \(1.5 kx_1^{0.5}\)
▶️Answer/Explanation
Ans: A
For a spring that is not linear (i.e., does not obey Hooke’s law) the energy stored is not \(\frac{1}{2} kx^2\). The magnitude of the energy stored will be equal to the magnitude of the work done to stretch the spring to \(x_1\)/ the steps to calculate the work are shown below.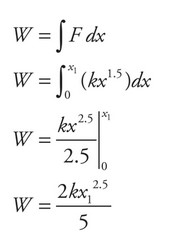
Question
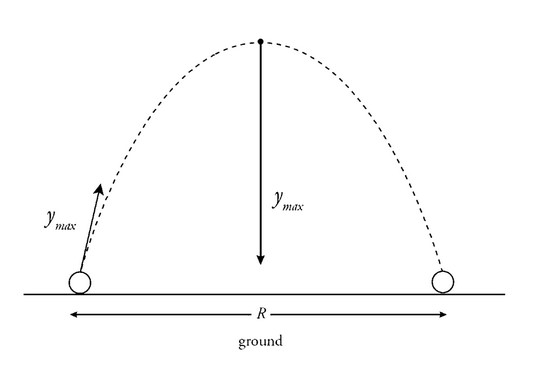
An ideal projectile is launched from the ground at an angle \(\theta \) to the horizontal, with an initial speed of \(v_o,\) The ground is flat and level everywhere. Write all answers in terms of \(v_o, \theta \),
and fundamental constants.
(a) Calculate the time the object is in the air.
(b) Calculate the maximum height the object reaches.
(c) What is the net vertical displacement of the object?
(d) Calculate the range (horizontal displacement) of the object.
(e) What should \(\theta\) be so that the projectile’s range is equal to its maximum vertical displacement?
▶️Answer/Explanation
This problem involves motion in two dimensions, so it’s important to begin by drawing a large picture of the situation. Note that our coordinate system is set up in the usual way with
x pointing to the right, y pointing up, and the origin at the point where the projectile is launched.
Next, draw a second diagram that splits \(\overheadarrow{v} _o \) into vertical and horizontal components. Note that you can use trigonometric properties to derive the values of \(v_{ox}\) and \(v_{oy}\).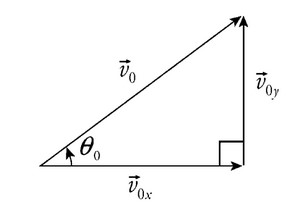
Now we’re ready to start answering the questions.
(a) For this problem, time of flight is determined by vertical quantities. This is because the flight ends when the object hits the ground, that is, when the y-coordinate is zero again.
If ~y = o, the projectile is either beginning or ending its flight.
You need to find t and you’re missing \(v_{f,y}\), so use Big Five #3.
\(\Delta y = v_{o,y}t + \frac{1}{2} a_u t^2\)
\(o = (v_o sin \theta) t + \frac{1}{2} (-g)t^2\)
\(\frac{1}{2} gt^2 – (v_o sin \theta) t =0\)
\(t(\frac{g}{2} t – v_o sin \theta ) = 0\)
At the beginning of the flight, t is equal to o. However, at the end of the flight, you would have the following:
\(\frac{g}{2} t – v_o sin \theta = 0\)
\(\frac{g}{2} t = v_o sin \theta \)
\(t = (\frac{2v_o sin \theta}{g})\)
The total amount of time in the air, then, is \((\frac{2v_0 sin \theta}{g}) – 0\), or just \((\frac{2v_o sin \theta}{g})\).
As an alternative, you could use Big Five # 2 to find the amount of time in which the projectile moves upward and then multiply that number by 2 to get the total time.
(b) As with the previous step, you are looking for a vertical quantity; because it’s t that you no longer care about and dy that you need, use Big Five # 5.
\(v_{fy}^2 = v_{oy}^2 + 2a (\Delta y)\)
At the top of the trajectory, \(v_{fy}=0\), which means you can now solve for \(\Delta y\).
\(o = v_{ou}^2 + 2a \Delta y\)
\(-v_{oy}^2 = 2a \Delta y\)
\(\frac{-v_{oy}^2}{2a}= \Delta y\)
If you plug in the known values of \(v_{oy}\) and a, you get the following:
\(\Delta y = \frac{-(v_o sin \theta )^2}{2(-g)}\)
\(\Delta y = \frac{v_0^2 sin^2 \theta}{2g}\)
Because \(u_o=0\), that value of \(\Delta y\) is also the value of \(y_{max}\)
(c) The object starts and ends on the ground (y = o), so its net
vertical displacement is o.
(d) You’re asked for a horizontal quantity, so let’s review our horizontal components.
\(\Delta x = ?\)
\(v_x = v_o cos \theta \)
\(t = \frac{2v_o sin \theta}{g}\)
Velocity is defined as \(v_x = \frac{\Delta x}{t}\), and this can be rewritten as \(\Delta x = v_x t\). You’ve found two of these values already, so plug them in and solve.
\(\Delta x = (v_o cos \theta ) (\frac{2v_0 sin \theta}{g})\)
\(\Delta x = \frac{2v_0^2 sin \theta cos \theta}{g}\)
(e) We’re told that the range equals the maximum vertical displacement, so \(\Delta x = y_{max}\)
\(\frac{2v_0^2 sin \theta cos \theta}{g} = \frac{v_o^2 sin^2 \theta}{2g}\)
Cancelling out form this equation, you’re left with the following:
\(2 cos \theta = \frac{sin \theta}{2}\)
\(4 = tan \theta\)
\(\theta = tan^{-1}(4)\)
You can check this by noting that the arctan of 4 is a fairly large angle (about 76°), which indicates that \(\overheadarrow{v}_0\) points more upward than rightward.