Question
For a particular nonlinear spring, the relationship between the magnitude of the applied force, F, and the stretch of the spring, x, is given by the equation \(F = kx^{1.5}\). How much energy is stored in the spring when is it stretched a distance \(x_1\)
(A) \(\frac{2k_1^{2.5}}{5}\)
(B) \(\frac{kx_1^{1.5}}{5}\)
(C) \(kx_1^{2.5}\)
(D) \(\frac{1}{2}kx_1^2\)
(E) \(1.5 kx_1^{0.5}\)
▶️Answer/Explanation
Ans: A
For a spring that is not linear (i.e., does not obey Hooke’s law) the energy stored is not \(\frac{1}{2} kx^2\). The magnitude of the energy stored will be equal to the magnitude of the work done to stretch the spring to \(x_1\)/ the steps to calculate the work are shown below.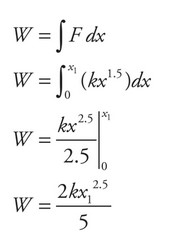
Question
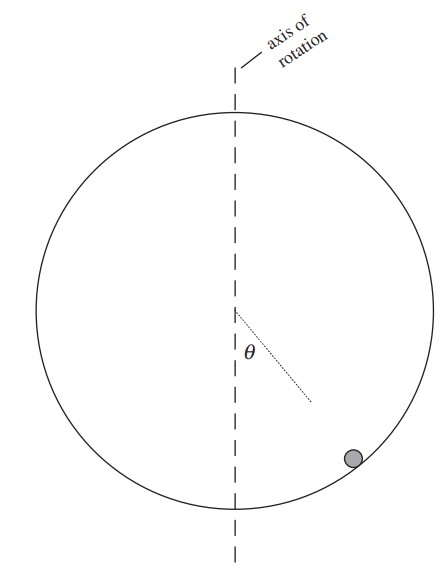
A hollow glass sphere of radius 8.0 cm rotates about a vertical diameter with frequency 5 revolutions per second. A small wooden ball of mass 2.0 g rotates inside the sphere, as shown in the diagram above.
(a) Draw a free-body diagram indicating the forces acting on the wooden ball when it is at the position shown in the picture above.
(b) Calculate the angle \(\theta \), shown in the diagram above, to which the ball rises.
(c) Calculate the linear speed of the wooden ball as it rotates.
(d) The wooden ball is replaced with a steel ball of mass 20 g. Describe how the angle \(\theta \) to which the ball rises will be affected. Justify your answer.
▶️Answer/Explanation
Ans:
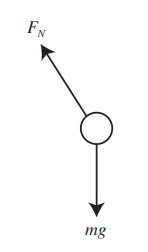
(a) 1 pt: The weight of the ball acts down.
1 pt: The normal force acts up and left, perpendicular to the surface of the glass.
1 pt: No other forces act.
(b) 1 pt: The normal force can be broken into vertical and horizontal components, where the vertical is \(F_{N}\cos \theta\) and the horizontal is \(F_{N}\sin \theta \). (The vertical direction goes with cosine here because \(\theta\) is measured from the vertical.)
1 pt: The net vertical force is zero because the ball doesn’t rise or fall on the glass. Setting up forces equal to down, \(F_{N}\cos \theta =mg\).
1 pt: The horizontal force is a centripetal force, so \(F_{N}\sin \theta =mv^{2}/r\sin \theta \).
1 pt: For using \(r\sin \theta \) and not just r. (Why? Because you need to use the radius of the actual circular motion, which is not the same as the radius of the sphere.)
1 pt: The tangential speed “v” is the circumference of the circular motion divided by the period. Since period is 1/f, and because the radius of the circular motion is \(r\sin \theta \), this speed \(v=2\pi r\sin \theta f\).
1 pt: Now divide the vertical and horizontal force equations to get rid of the \(F_{N}\) term: \(\sin \theta /\cos \theta =v^{2}/r\sin \theta g\).
1 pt: Plug in the speed and the sin q terms cancel, leaving \(\cos \theta =g/4\pi ^{2}rf^{2}\).
1 pt: Plugging in the given values (including r = 0.08 m), q = 83°.
(c) 1 pt: From part (a), the linear speed is \(2\pi r\sin \theta f\).
1 pt: Plugging in values, the speed is 2.5 m/s. (If you didn’t get the point in part (a) for figuring out how to calculate linear speed, but you do it right here, then you can earn the point here.)
(d) 1 pt: The angle will not be affected.
1 pt: Since the mass of the ball does not appear in the equation to calculate the angle in part (b), the mass does not affect the angle.
