Question
For a particular nonlinear spring, the relationship between the magnitude of the applied force, F, and the stretch of the spring, x, is given by the equation \(F = kx^{1.5}\). How much energy is stored in the spring when is it stretched a distance \(x_1\)
(A) \(\frac{2k_1^{2.5}}{5}\)
(B) \(\frac{kx_1^{1.5}}{5}\)
(C) \(kx_1^{2.5}\)
(D) \(\frac{1}{2}kx_1^2\)
(E) \(1.5 kx_1^{0.5}\)
▶️Answer/Explanation
Ans: A
For a spring that is not linear (i.e., does not obey Hooke’s law) the energy stored is not \(\frac{1}{2} kx^2\). The magnitude of the energy stored will be equal to the magnitude of the work done to stretch the spring to \(x_1\)/ the steps to calculate the work are shown below.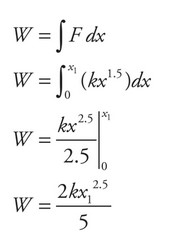
Question

The velocity of an object before a collision is directed straight north and the velocity after the collision is directed straight west as shown above. Which of the following vectors represents the change in momentum of the object?

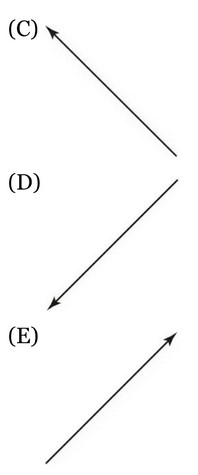
▶️Answer/Explanation
Ans: D
The direction of the change in momentum of an object will be the direction of \(\Delta v\). The resultant of \(v_2 – v_1\) is shown below.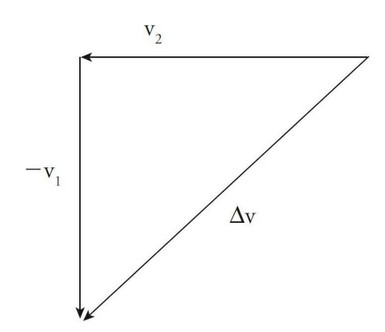
Question
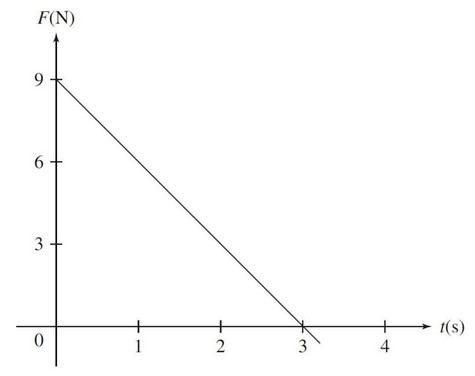
A block of mass 2 kg, initially at rest, is pulled along a frictionless, horizontal surface with a force shown as a function of time by the graph above.
The speed of the block at t = 3 s is
(A) 0 m/s
(B) 4.5 m/s
(C) 6.75 m/s
(D) 13.5 m/s
(E) 54 m/s
▶️Answer/Explanation
Ans: C
We will use the impulse-momentum theorem here. We cannot use the constant acceleration equations with the acceleration from question 5 because the acceleration is not constant. The area between the graph and the x-axis is the impulse.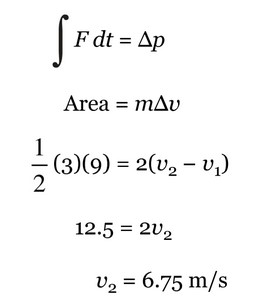
Question
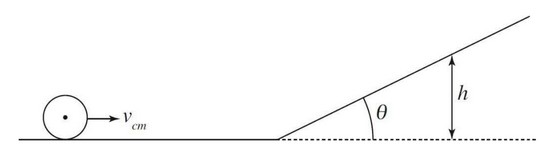
The center of mass of a cylinder of mass m, radius r, and rotational inertia \(I = \frac{1}{2} mr^2\) has a velocity of \(v_{cm}\) as it rolls without slipping along a horizontal surface. It then encounters a ramp of angle \(\theta \), and continues to roll up the ramp without slipping.
Now the cylinder is replaced with a hoop that has the same mass and radius. The hoop’s rotational inertia is \(mr^2\). The center of mass of the hoop has the same velocity as the cylinder when it is rolling along the horizontal surface and the hoop also rolls up the ramp without slipping. How would the maximum height of the cylinder?
(A) The hoop would reach a greater maximum height than the cylinder.
(B) The hoop and cylinder would reach the same maximum height.
(C) The cylinder would reach a greater maximum height than the hoop.
(D) The cylinder would reach less than half the height of the hoop.
(E) None of the above.
▶️Answer/Explanation
Ans: A
Again we will use the Law of Conservation of Energy. The easiest way to determine which object will reach a greater height is to determine which object has more kinetic energy as it rolls along the horizontal surface. If both the cylinder and the hoop have the same velocity then the hoop will have more total kinetic energy because it has a greater rotational inertia. The calculation at the top of the next page shows the calculation for the height which also shows that the hoop reaches a greater height.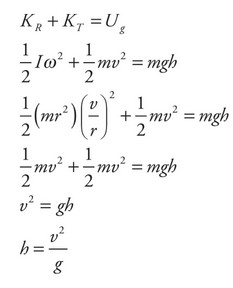
While both (A) and (D) indicate that the hoop reaches a greater maximum height than the cylinder, (D) is incorrect as the cylinder reaches 3/4 the height of the hoop.
Question
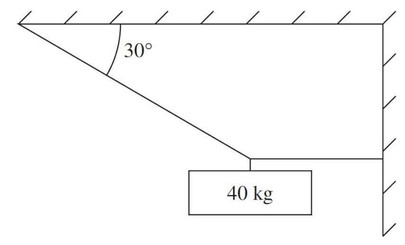
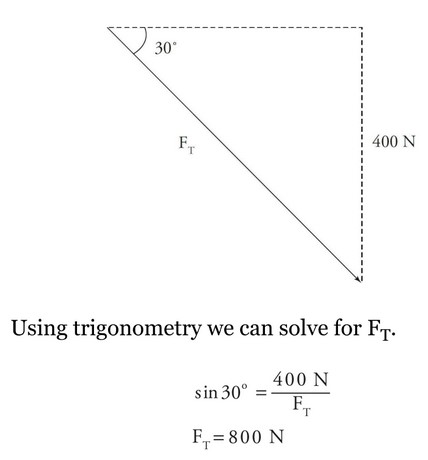
An object of mass 40 kg is suspended by means of two cords, as shown above. The tension in the angled cord is
(A) 80 N
(B) 230 N
(C) 400 N
(D) 690 N
(E) 800 N
▶️Answer/Explanation
Ans: E
The mass is in static equilibrium so the net force in all directions is zero. Using the sum of the forces in the vertical direction, one can conclude that the vertical component of the slanted cord must equal the force of gravity of the mass. That produces the following triangle for the tension in the slanted cord.