IIT JEE Main Maths -Unit 10 -Circle, Conic Sections- Exam Style Questions- New Syllabus

Question

Let the parabola $y = x^2 + px – 3$ meet the coordinate axes at the points $P, Q, R$. If the circle with centre at $(-1,-1)$ passes through $P, Q, R$, then the area of $\triangle PQR$ is:

$(1)\ 4$

$(2)\ 6$

$(3)\ 7$

$(4)\ 5$

▶️ Answer/Explanation

Circle: $(x+1)^2 + (y+1)^2 = r^2$, passing through $(0,-3)$ gives $r^2 = 5$.

Intersection with $y=0$ gives $x=1$ and $x=-3$. So $P(1,0), Q(-3,0), R(0,-3)$.

Area = $\dfrac{1}{2} |1(0+3) + (-3)(-3+0) + 0(0-0)| = 6$.

The correct answer is 6.

Question

A circle C of radius 2 lies in the second quadrant and touches both the coordinate axes. Let r be the radius of a circle that has centre at the point (2, 5) and intersects the circle C at exactly two points. If the set of all possible values of r is the interval $(\alpha, \beta)$, then $3\beta – 2\alpha$ is equal to :

$(1)\ 15$

$(2)\ 14$

$(3)\ 12$

$(4)\ 10$

▶ Answer/Explanation

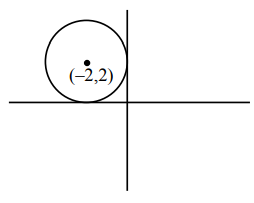
$S_1: (x + 2)^2 + (y – 2)^2 = 2^2$
$S_2: (x – 2)^2 + (y – 5)^2 = r^2$

Both circles intersect at two points $\Rightarrow |r – 2| < 5 < 2 + r$ $\Rightarrow 3 < r < 7$
$r \in (3, 7)$
$\alpha = 3, \ \beta = 7$
$3\beta – 2\alpha = 15$

The correct answer is $(1)\ 15$.

Question

Let the foci of a hyperbola be $ (1, 14) $ and $ (1, -12) $. If it passes through the point $ (1, 6) $, then the length of its latus-rectum is :
(1) $ \frac{25}{6} $
(2) $ \frac{24}{5} $
(3) $ \frac{288}{5} $
(4) $ \frac{144}{5} $

▶️ Answer/Explanation

Ans. (3)

Sol.

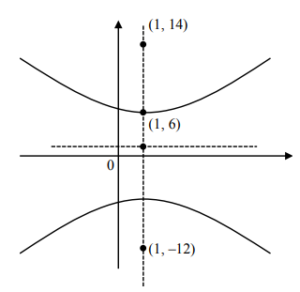
$ be = 13, b = 5 $

$ a^2 = b^2 (e^2 – 1) $

$ = b^2 e^2 – b^2 $

$ = 169 – 25 = 144 $

$ LR = \frac{2a^2}{b} = \frac{2 \times 144}{5} = \frac{288}{5} $

Question

The area of the region, inside the circle $ (x – 2)^2 + y^2 = 12 $ and outside the parabola $ y^2 = 2\sqrt{3} x $ is :
(1) $ 6\pi – 8 $
(2) $ 3\pi – 8 $
(3) $ 6\pi – 16 $
(4) $ 3\pi + 8 $

▶️ Answer/Explanation

Ans. (3)

Sol.

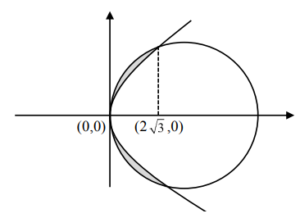
$ y^2 = 2\sqrt{3} x $

$ (x – 2)^2 + y^2 = 2\sqrt{3} x $

$ A = 2 \int_{0}^{2/\sqrt{3}} \left( \sqrt{12 – (x – 2)^2} – \sqrt{2\sqrt{3} x} \right) \, dx $

$ = \pi \times \left[ x – 2\sqrt{3} \right]_{0}^{2/\sqrt{3}} – \left[ 2\sqrt{2\sqrt{3} x} \right]_{0}^{2/\sqrt{3}} $

$ = 6\pi – 16 $

Question

Let $P(4, 4\sqrt{3})$ be a point on the parabola $y^2 = 4ax$ and $PQ$ be a focal chord of the parabola. If $M$ and $N$ are the foot of perpendiculars drawn from $P$ and $Q$ respectively on the directrix of the parabola, then the area of the quadrilateral $PQMN$ is equal to:
(1) $\frac{263\sqrt{3}}{8}$
(2) $17\sqrt{3}$
(3) $\frac{343\sqrt{3}}{8}$
(4) $\frac{34\sqrt{3}}{3}$

▶ Answer/Explanation

Ans. (3)
Sol. $S$ $O$ $N$ $Q$ $M$

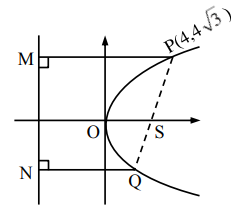
$(4, 4\sqrt{3})$ lies on $y^2 = 4ax$ $\Rightarrow 48 = 4a.4$
$4a = 12$ $\Rightarrow y^2 = 12x$ is equation of parabola
Now, parameter of $P$ is $t_1 = 2\sqrt{3}$
$\Rightarrow$ Parameters of $Q$ is $t_2 = -\frac{\sqrt{3}}{2}$ $\Rightarrow Q (\frac{9}{4}, -3\sqrt{3})$
Area of trapezium $PQNM$
= $\frac{1}{2} MN.(PM + QN)$
= $\frac{1}{2} MN.(PS + QS)$
= $\frac{1}{2} MN.PQ$
= $\frac{1}{2} \frac{49}{4} \sqrt{3}.7\sqrt{3}$
($\frac{343}{2} \frac{1}{4} \frac{1}{8}$ = $\frac{343\sqrt{3}}{8}$ = 3 )

Question

The area of the region enclosed by the curves $y = x^2 – 4x + 4$ and $y^2 = 16 – 8x$ is :
(1) $\frac{8}{3}$
(2) $\frac{4}{3}$
(3) 5
(4) 8

▶ Answer/Explanation

Ans. (1)
Sol.

$y = (x – 2)^2$, $y^2 = 8(x – 2)$
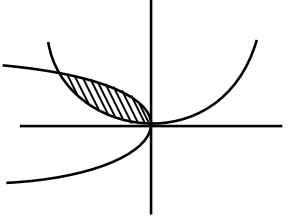
$y = x^2$, $y^2 = -8x$
$\frac{16ab}{3} = \frac{16 \times \frac{1}{4} \times 2}{3} = \frac{8}{3}$

Question

4. If the line $ 3x – 2y + 12 = 0 $ intersects the parabola $ 4y = 3x^2 $ at the points A and B, then at the vertex of the parabola, the line segment AB subtends an angle equal to

(1) $ \tan^{-1}\!\left(\frac{1}{9}\right) $ \quad
(2) $ \pi – \tan^{-1}\!\left(\frac{3}{2}\right) $ \quad
(3) $ \tan^{-1}\!\left(\frac{1}{4}\right) $ \quad
(4) $ \tan^{-1}\!\left(\frac{1}{9/7}\right) $

▶️ Answer/Explanation

Ans. (4)

Sol.

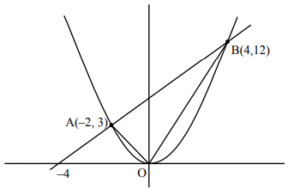
$ 3x – 2y + 12 = 0 $
$ 4y = 3x^2 $

$ \therefore 2(3x + 12) = 3x^2 $

$ \Rightarrow x^2 – 2x – 8 = 0 $

$ \Rightarrow x = -2, 4 $

$ m_{OA} = -\frac{3}{2}, \; m_{OB} = 3 $

$ \tan\theta = \left| \frac{3 – (-\frac{3}{2})}{1 + (-\frac{3}{2})(3)} \right| = \frac{9}{7} $

$ \therefore \theta = \tan^{-1}\!\left(\frac{9}{7}\right) $

Question

Let the circle C touch the line $x – y + 1 = 0$, have the centre on the positive x-axis, and cut off a chord of length $\frac{4\sqrt{13}}{5}$ along the line $-3x + 2y = 1$. Let H be the hyperbola $\frac{x^2}{\alpha^2} – \frac{y^2}{\beta^2} = 1$, whose one of the foci is the centre of C and the length of the transverse axis is the diameter of C. Then $2\alpha^2 + 3\beta^2$ is equal to ________

▶️ Answer/Explanation

Ans. (19)

Sol.

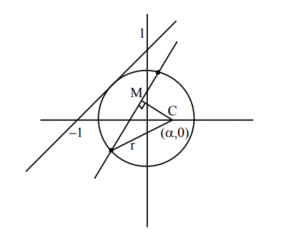
$ x – y + 1 = 0; \; p = r $

$ \left| \frac{\alpha – 0 + 1}{\sqrt{2}} \right| = r \Rightarrow (\alpha + 1)^2 = 2r^2 $ ….(1)

Now
$ \left( \frac{-3\alpha + 0 – 1}{\sqrt{9 + 4}} \right)^2 + \left( \frac{2}{\sqrt{13}} \right)^2 = r^2 $

$ \Rightarrow (3\alpha + 1)^2 + 4 = 13r^2 $ ….(2)

(1) & (2) $ \Rightarrow (3\alpha + 1)^2 + 4 = 13 \cdot \frac{(\alpha + 1)^2}{2} $

$ \Rightarrow 18\alpha^2 + 12\alpha + 2 + 8 = 13\alpha^2 + 26\alpha + 13 $

$ \Rightarrow 5\alpha^2 – 14\alpha – 3 = 0 $

$ \Rightarrow 5\alpha^2 – 15\alpha + \alpha – 3 = 0 \Rightarrow 5\alpha(\alpha – 3) + (\alpha – 3) = 0 $

$ \Rightarrow \alpha = -\frac{1}{5}, \, 3 $

$ \therefore r = 2\sqrt{2} $

Now $ \alpha e = 3 $ and $ 2\alpha = 4\sqrt{2} $

$ \alpha^2 e^2 = 9 \Rightarrow \alpha e = 2\sqrt{2} \Rightarrow \alpha^2 = 8 $

$ \alpha^2 \left( 1 + \frac{\beta^2}{\alpha^2} \right) = 9 $

$ \alpha^2 + \beta^2 = 9 $

$ \beta^2 = 1 $

$ \therefore 2\alpha^2 + 3\beta^2 = 2(8) + 3(1) = 19 $

IIT JEE Main Maths -Unit 10 -Circle, Conic Sections- Exam Style Questions- New Syllabus

Resources

Members

Company